多项式回归

非线性回归是用一条曲线或者曲面去逼近原始样本在空间中的分布，它“贴近”原始分布的能力一般较线性回归更强。

多项式是由称为不定元的变量和称为系数的常数通过有限次加减法、乘法以及自然数幂次的乘方运算得到的代数表达式。

多项式回归（Polynomial Regression）是研究一个因变量与一个或多个自变量间多项式关系的回归分析方法。多项式回归模型是非线性回归模型中的一种。

由泰勒级数可知，在某点附近，如果函数n次可导，那么它可以用一个n次的多项式来近似。

假设确定了用一个一元n次多项式来拟合训练样本集，模型可表示如下：

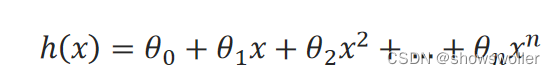
那么多项式回归的任务就是估计出各θ值。

包括多项式回归问题在内的一些非线性回归问题可以转化为线性回归问题来求解，具体思路是将式中的每一项看作一个独立的特征（或者说生成新的特征），令y_1=x,y_2=x^2,…,y_n=x^n,那么一个一元n次多项式θ_0+θ_1x+θ_2x^2+…+θ_nx^n就变成了一个n元一次多项式θ_0+θ_1y_1+θ_2y_2+…+θ_ny_n，就可以采用线性回归的方法来求解。

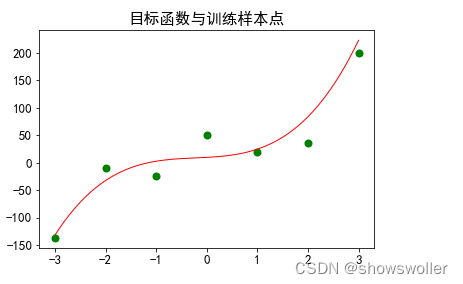
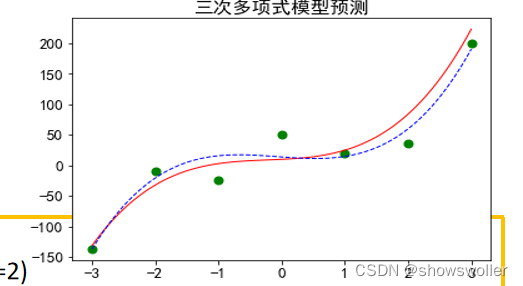
示例：先拟定一个一元三次多项式作为目标函数，然后再加上一些噪声产生样本集，再用转化的线性回归模型来完成拟合，最后对测试集进行预测。

测试效果如下

部分代码如下

def myfun(x):
    input:x(float):自变量
    output:函数值'''
    return 10 + 5 * x + 4 * x**2 + 6 * x**3

import numpy as np
x = np.linspace(-3,3, 7)
>>> array([-3., -2., -1.,  0.,  1.,  2.,  3.])
x_p = (np.linspace(-2.5, 2.5, 6)).reshape(-1,1) # 预测点
import random
y = myfun(x) + np.random.random(size=len(x)) * 100 - 50
y
>>> array([-136.49570384,   -8.98763646,  -23.33764477,   50.97656894,
         20.19888523,   35.76052266,  199.48378741])
from sklearn.preprocessing import PolynomialFeatures
featurizer_3 = PolynomialFeatures(degree=3)
x_3 = featurizer_3.fit_transform(x)
x_3
>>>array([[  1.,  -3.,   9., -27.],
       [  1.,  -2.,   4.,  -8.],
       [  1.,  -1.,   1.,  -1.],
       [  1.,   0.,   0.,   0.],
       [  1.,   1.,   1.,   1.],
       [  1.,   2.,   4.,   8.],
       [  1.,   3.,   9.,  27.]])

局部回归

前述的回归模型，假设所有样本之间都存在相同程度的影响，这类模型称为全局模型。在机器学习中，还有另一种思想：认为相近的样本相互影响更大，离的远的样本相互影响很小，甚至可以不计。这种以“远亲不如近邻”思想为指导得到的模型称为局部模型。局部思想在聚类、回归、分类等机器学习任务中都有应用，聚类算法中的DBSCAN算法就是以这种思想为指导的模型。

用于回归的局部模型有局部加权线性回归模型、K近邻模型和树回归模型等。

局部加权线性回归（Locally Weighted Linear Regression，LWLR）模型根据训练样本点与预测点的远近设立权重，离预测点越近的点的权重就越大。局部加权线性回归方法不形成固定的模型，对每一个新的预测点，都需要计算每个样本点的权值，在样本集非常大的时候，预测效率较低。