代码随想录刷题记录day46 最长递增子序列+最长连续递增序列+最长重复子数组
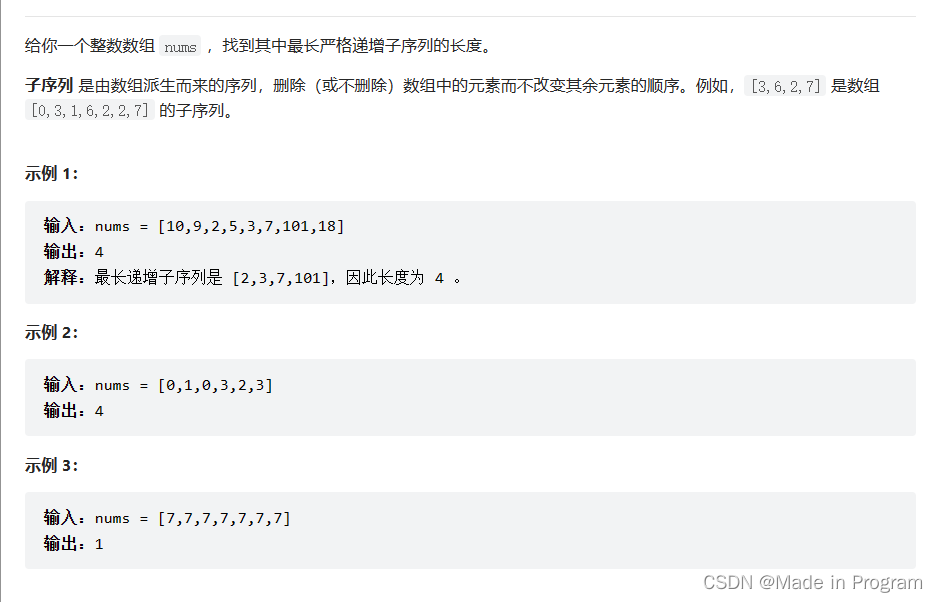
300. 最长递增子序列
思想
1.dp数组的定义
dp[i]表示[0,i]区间的最长递增子序列
2.递推公式
如果num[i]>num[j];dp[i]=dp[j]+1
其中j从0到i-1遍历
3.初始化
所有的都初始化为1
4.遍历顺序
从前到后 依靠前一个的状态
5.打印数组
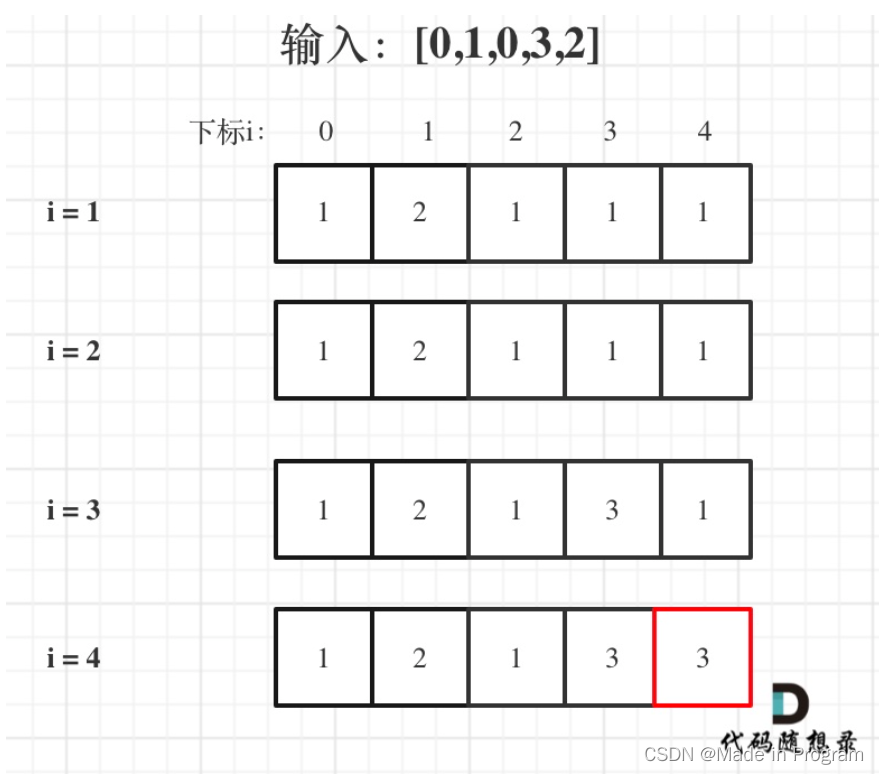
代码
class Solution {
public int lengthOfLIS(int[] nums) {
//dp数组的定义
//dp[i]表示[0,i]区间的最长严格递增子序列的长度
//递归公式
//dp[i]=从0到i-1的最长子序列+1
//初始化
int[] dp=new int[nums.length];
Arrays.fill(dp,1);
int res=0;
if(nums.length<=1) return nums.length;
for(int i=1;i<nums.length;i++){
for(int j=0;j<i;j++){
if(nums[i]>nums[j]){
dp[i]=Math.max(dp[j]+1,dp[i]);
}
}
//System.out.println(dp[i]);
if(dp[i]>res) res=dp[i];
}
return res;
}
}
674. 最长连续递增序列

思想
方法1:
应该叫做贪心?
维护一个变量 le记录连续的长度,res记录最大的连续的长度
public int findLengthOfLCIS(int[] nums) {
//方法1 暴力遍历
int res=1;
int le=1;
for(int i=1;i<nums.length;i++){
if(nums[i]>nums[i-1]){
le++;
}else{
le=1;//重新开始计数
}
if(le>res){
res=le;
}
}
return res;
}
方法2 动态规划
1.dp数组的定义
dp[i]表示以i为结尾的数组的最长连续递增序列
2.递推公式
if(nums[i]>nums[i-1]) dp[i]=dp[i-1]+1
3.初始化
都初始化为1
4.遍历顺序
从1开始
5.数组打印

718. 最长重复子数组
思想
1.数组定义
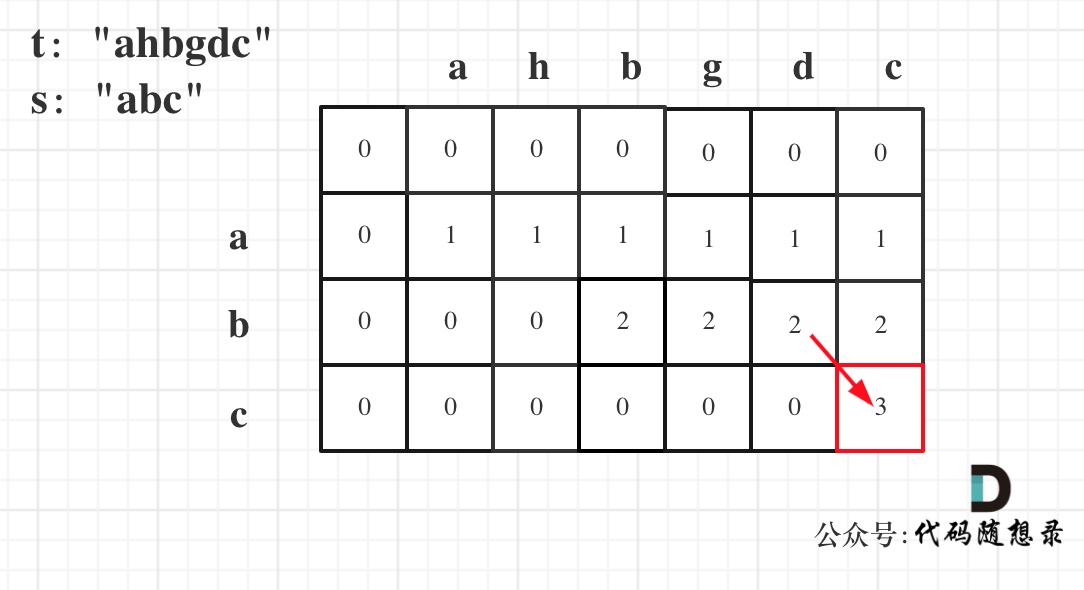
dp[i][j] 表示以i-1结尾的数组nums1和以j-1的数组nums2的最长重复子数组的长度
2.递推公式
if(nums1[i-1]=nums[j-1]) dp[i][j]=dp[i-1][j-1]+1
3.初始化
如果nums1[0]=nums2[0] dp[1][1]=dp[0][0]+1 所以dp[0][0]=0;
4.遍历顺序
nums1数组从1开始 内层nums数组从1开始
5.数组打印
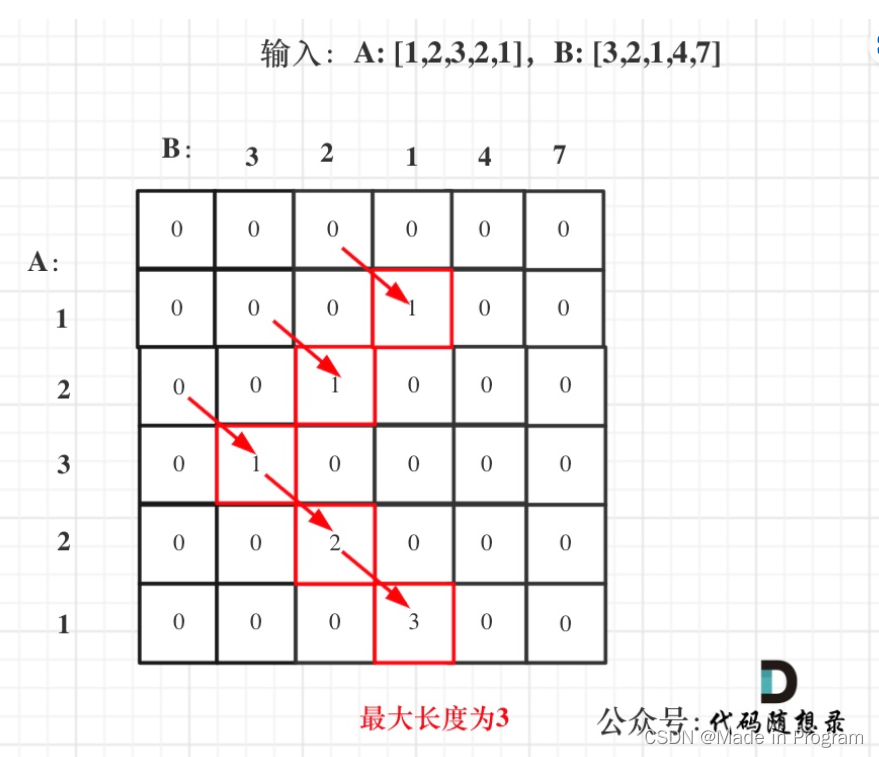
代码
class Solution {
public int findLength(int[] nums1, int[] nums2) {
//1.dp数组的定义
//dp[i][j] 以i-1结尾的数组nums1和以j-1的数组nums2的最长重复子数组的长度
//2.递推公式
//当nums1[i-1]=nums2[j-1], dp[i][j]=dp[i-1][j-1]+1
//3.初始化
//dp[0][0] 无意义,
// 如果nums1[0]=nums2[0] dp[1][1]=dp[0][0]+1 所以dp[0][0]=0;
int[][] dp = new int[nums1.length+1][nums2.length+1];
int res=0;
for(int i=1;i<=nums1.length;i++){
for(int j=1;j<=nums2.length;j++){
if(nums1[i-1]==nums2[j-1]) dp[i][j]=dp[i-1][j-1]+1;
if(dp[i][j]>res) res=dp[i][j];
}
}
return res;
}
}