开始背包问题的练习！

1. 背包问题的理论基础

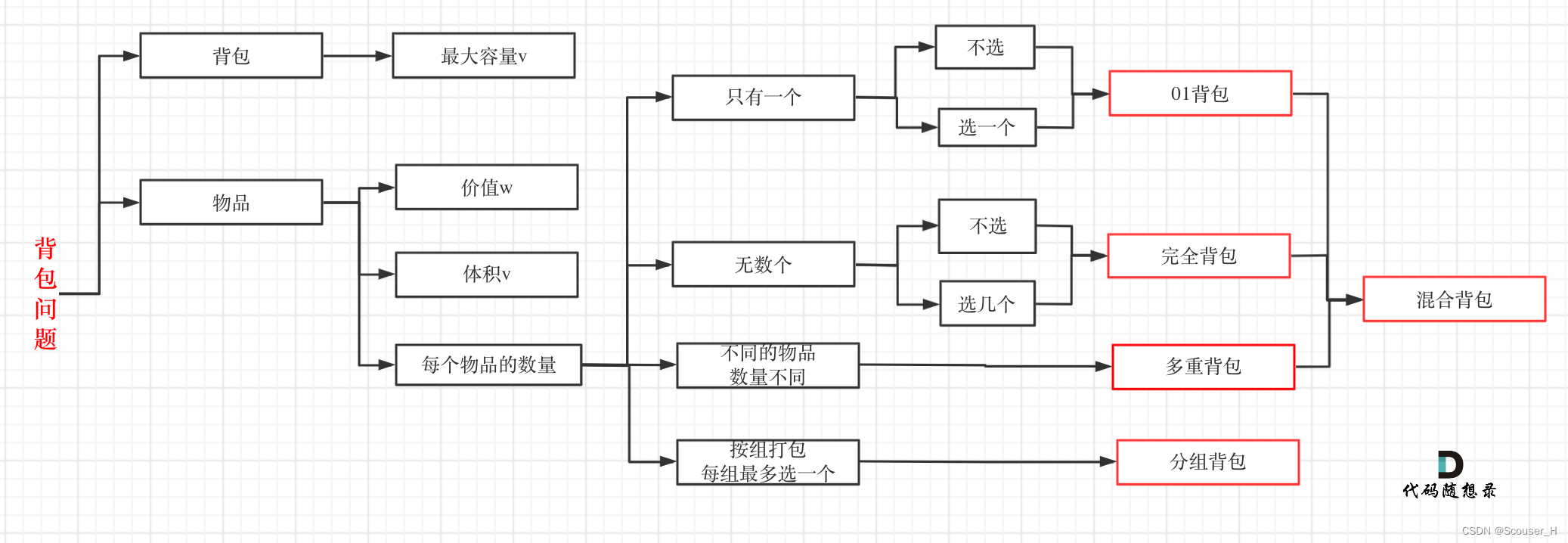
对于面试的话，其实掌握01背包，和完全背包，就够用了，最多可以再来一个多重背包。这里附上代码随想录的图，可以对背包问题进行一个分类。

1.1 十分重要的基础：01背包

比如这样的题：有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

这是标准的背包问题，以至于很多同学看了这个自然就会想到背包，甚至都不知道暴力的解法应该怎么解了。

这样其实是没有从底向上去思考，而是习惯性想到了背包，那么暴力的解法应该是怎么样的呢？

每一件物品其实只有两个状态，取或者不取，所以可以使用回溯法搜索出所有的情况，那么时间复杂度就是$o(2^n)$，这里的n表示物品数量。

所以暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化！

1.2 二维dp数组01背包

依然动规五部曲分析一波。

1. 确定dp数组以及下标的含义

对于背包问题，有一种写法， 是使用二维数组，即dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

2. 确定递推公式

再回顾一下dp[i][j]的含义：从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

那么可以有两个方向推出来dp[i][j]，

• 不放物品i：由dp[i - 1][j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以背包内的价值依然和前面相同。)
• 放物品i：由dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值

所以递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

3. dp数组如何初始化

关于初始化，一定要和dp数组的定义吻合，否则到递推公式的时候就会越来越乱。

首先从dp[i][j]的定义出发，如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。

再看其他情况：状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来，那么i为0的时候就一定要初始化。

dp[0][j]，即：i为0，存放编号0的物品的时候，各个容量的背包所能存放的最大价值。

那么很明显当 j < weight[0]的时候，dp[0][j] 应该是 0，因为背包容量比编号0的物品重量还小。

当j >= weight[0]时，dp[0][j] 应该是value[0]，因为背包容量放足够放编号0物品。

4. 确定遍历顺序

先遍历 物品还是先遍历背包重量呢？其实都可以！！ 但是先遍历物品更好理解。

5. 举例推导dp数组

做动态规划的题目，最好的过程就是自己在纸上举一个例子把对应的dp数组的数值推导一下，然后在动手写代码！

最后的Python代码如下

def test_2_wei_bag_problem1(weight, value, bagweight):
    # 二维数组
    dp = [[0] * (bagweight + 1) for _ in range(len(weight))]

    # 初始化
    for j in range(weight[0], bagweight + 1):
        dp[0][j] = value[0]

    # weight数组的大小就是物品个数
    for i in range(1, len(weight)):  # 遍历物品
        for j in range(bagweight + 1):  # 遍历背包容量
            if j < weight[i]:
                dp[i][j] = dp[i - 1][j]
            else:
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])

    return dp[len(weight) - 1][bagweight]

if __name__ == "__main__":

    weight = [1, 3, 4]
    value = [15, 20, 30]
    bagweight = 4

    result = test_2_wei_bag_problem1(weight, value, bagweight)
    print(result)

1.3 一维滚动数组动态规划

对于背包问题其实状态都是可以压缩的。

在使用二维数组的时候，递推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上，表达式完全可以是：dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);

与其把dp[i - 1]这一层拷贝到dp[i]上，不如只用一个一维数组了，只用dp[j]（一维数组，也可以理解是一个滚动数组）。

这就是滚动数组的由来，需要满足的条件是上一层可以重复利用，直接拷贝到当前层。

读到这里估计大家都忘了 dp[i][j]里的i和j表达的是什么了，i是物品，j是背包容量。

dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

def test_1_wei_bag_problem(weight, value, bagWeight):
    # 初始化
    dp = [0] * (bagWeight + 1)
    for i in range(len(weight)):  # 遍历物品
        for j in range(bagWeight, weight[i] - 1, -1):  # 遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i])

    return dp[bagWeight]


if __name__ == "__main__":

    weight = [1, 3, 4]
    value = [15, 20, 30]
    bagweight = 4

    result = test_1_wei_bag_problem(weight, value, bagweight)
    print(result)

2. 练习题

416. Partition Equal Subset Sum

Given an integer array nums, return true if you can partition the array into two subsets such that the sum of the elements in both subsets is equal or false otherwise.

只有确定了如下四点，才能把01背包问题套到本题上来。

• 背包的体积为sum / 2
• 背包要放入的商品（集合里的元素）重量为 元素的数值，价值也为元素的数值
• 背包如果正好装满，说明找到了总和为 sum / 2 的子集。
• 背包中每一个元素是不可重复放入。

以上分析完，我们就可以套用01背包，来解决这个问题了。

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        _sum = 0

        dp = [0] * 10001
        for num in nums:
            _sum += num
        if _sum % 2 == 1:
            return False
        target = _sum // 2
        for num in nums:
            for j in range(target, num - 1, -1): 
                dp[j] = max(dp[j], dp[j - num] + num)

        if dp[target] == target:
            return True
        return False