题目描述：

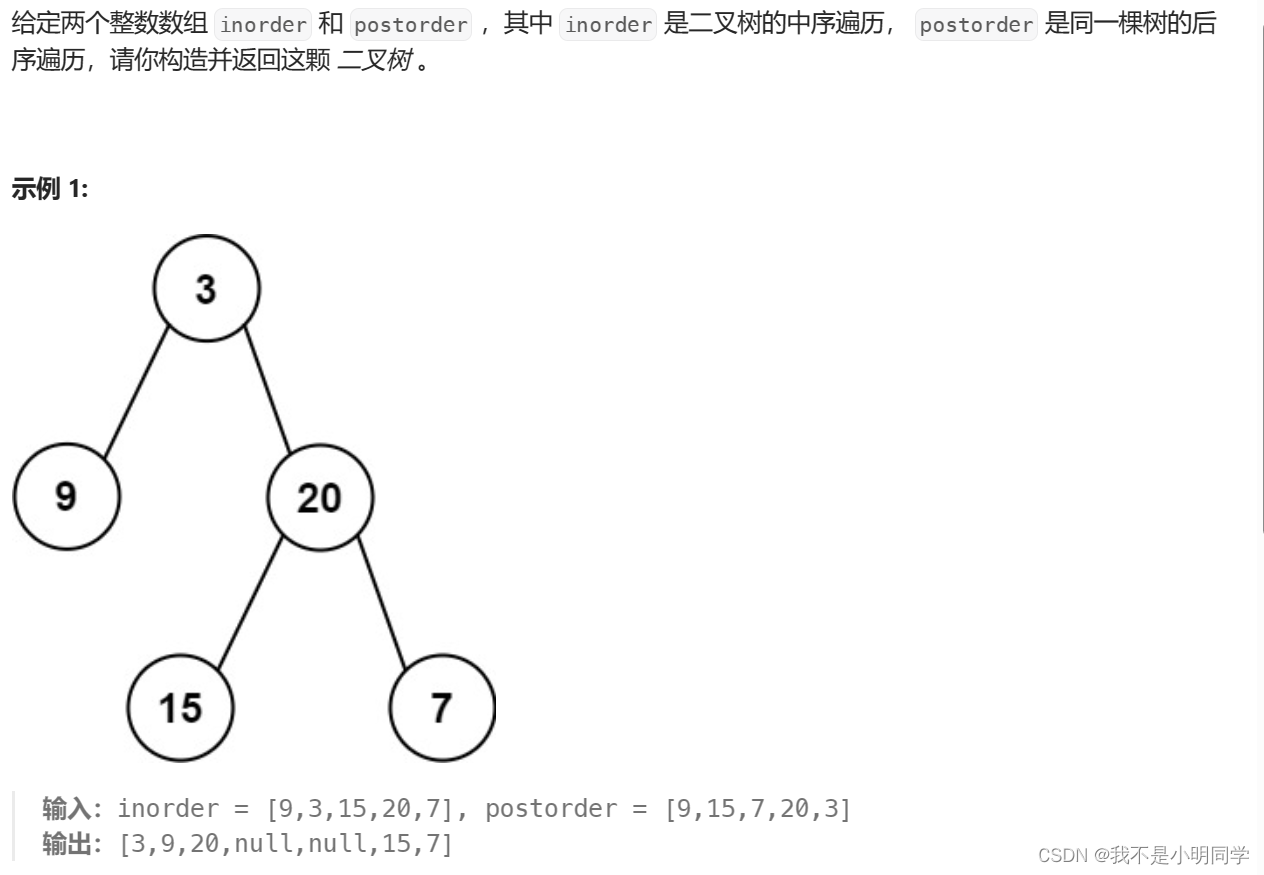
思路分析：

后序遍历分析图

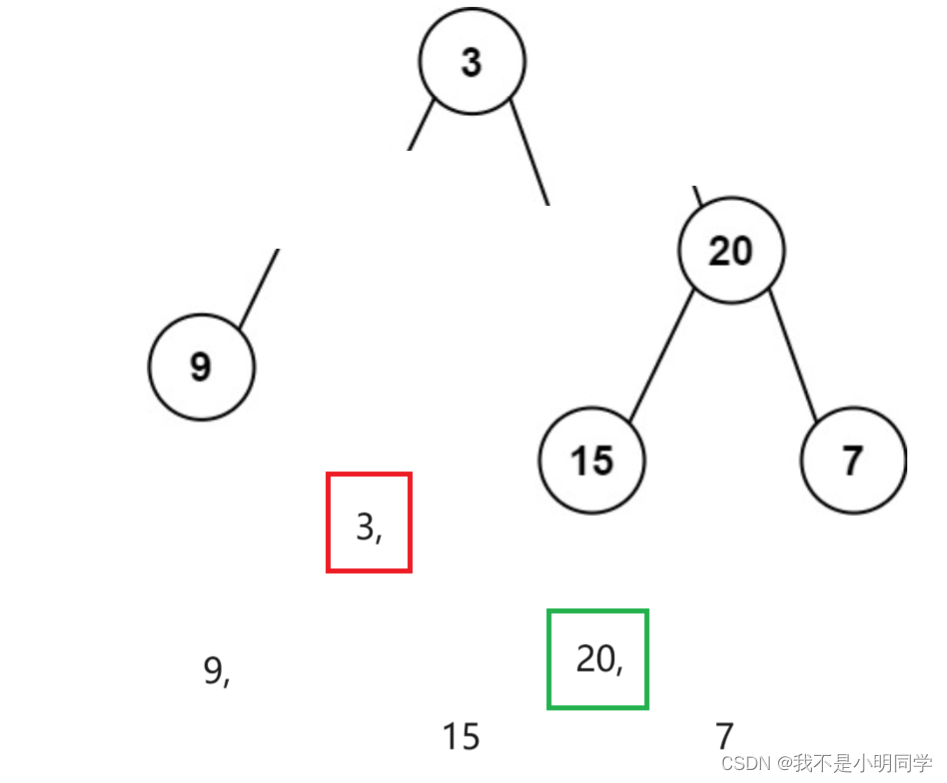中序遍历分析图

不难看出后序遍历的结果中的最后一个元素就是根节点，倒数第二个元素则是根节点的右子树的根节点，而倒数第三个元素是右子树的新右子树的根节点，依次类推。我们可以根据这一特性先构造二叉树的右子树。

接下来我们再分析一下中序遍历，如图所示，我们将二叉树和中序遍历结果拆开后发现，在中序遍历中根节点的左侧数据则恰好是二叉树的左子树，而根节点的右侧数据恰好是二叉树的右子树。根据中序遍历和后序遍历的规律，那么我们就可以将这个还原二叉树的过程分为两大步骤：

1. 在后序遍历中找根节点；2. 在中序遍历中找到根节点；3. 构建子树。接下来我们详细分析一下这个过程。

1. 寻找根节点，我们根据 postorder 数组从后往前开始找根节点，第一个节点即为 postorder[postorder.length-1]。第一个节点比较容易找到，但是其他的节点就没有那么容易，因此我们准备了一个 index 用来记录找到了多少个节点，这样在找后面的节点的时候我们只需要找postorder[postorder.length-1-index] 就可以了。

2. 在 inorder 数组中找到根节点 rootIndex 的位置，这一步骤非常重要，是接下来构建根节点的子树的前提，rootIndex 的左边是左子树，rootIndex 的右边是右子树。

3. 构建右子树，左子树。必须要先构建右子树，因为 postorder 从后往前的顺序就是右子树在先，左子树在后。

代码示例：

class Solution {
    public int index = 0;
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        int len = postorder.length-1;
        return createChild(inorder,postorder,0,inorder.length-1,len);
    }
    public int findIndex(int[] inorder,int val,int beg, int end) {
        for(int i = beg; i <= end; i++) {
            if(inorder[i] == val) return i;
        }
        return -1;
    }
    public TreeNode createChild(int[] inorder,int[] postorder,int beg,int end,int len) {
        if(beg > end) return null;
        
        TreeNode root = new TreeNode(postorder[len-index]);
        // 在中序遍历数组中找到 root 的值的位置
        int rootIndex = findIndex(inorder,postorder[len-index],beg,end);
        index++;
        root.right = createChild(inorder,postorder,rootIndex+1,end,len);
        root.left = createChild(inorder,postorder,beg,rootIndex-1,len);

        return root;
    }
}