1.二叉搜索树的概念
二叉搜索树又称二叉排序树,它或者是一颗空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有的节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
如图所示:
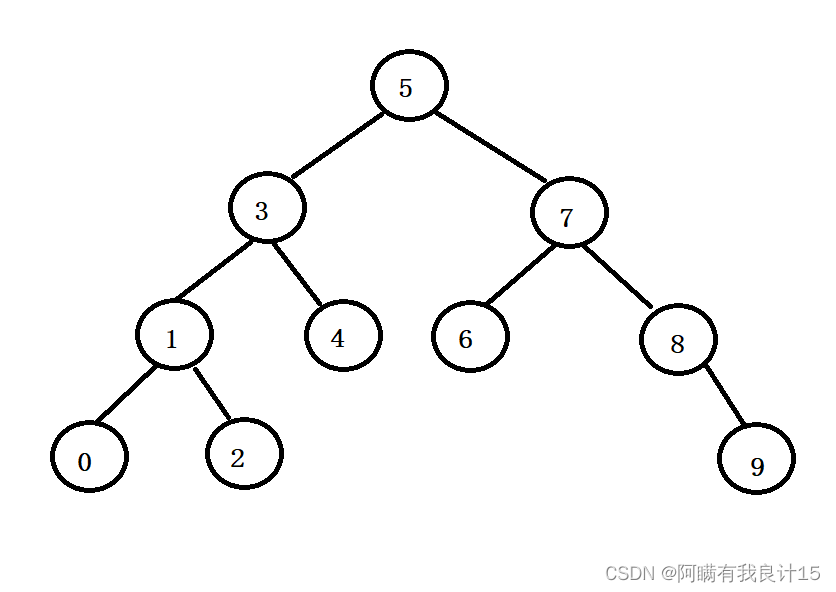
二叉搜索树的性质:
1.二叉搜索树中最左侧的节点是树中最小的节点,最右侧节点一定是树中最大的节点
2.采用中序遍历遍历二叉搜索树,可以得到一个有序的序列
2.二叉搜索树的实现:
package test;
import java.util.LinkedList;
class TreeNode {
int val;
TreeNode leftChild;
TreeNode rightChild;
public TreeNode(int val) {
this.val = val;
}
public void printNode() {
System.out.println(val);
}
}
public class BinarySearchTree {
//创建一颗二叉搜索树
public TreeNode root;
//构造方法初始化根节点值
public BinarySearchTree(int val) {
root = new TreeNode(val);
}
//插入
public void insert(int val) {
TreeNode node = new TreeNode(val);
TreeNode cur;
if (root == null) {
root = node;
return;
} else {
cur = root;
while (true) {
if (val >= cur.val) {
if (cur.rightChild == null) {
cur.rightChild = node;
return;
} else {
cur = cur.rightChild;
}
} else {
if (cur.leftChild == null) {
cur.leftChild = node;
return;
} else {
cur = cur.leftChild;
}
}
}
}
}
//查找指定节点
public TreeNode find(int val) {
TreeNode cur = root;
while (cur != null) {
if (val < cur.val) {
cur = cur.leftChild;
} else if (val > cur.val) {
cur = cur.rightChild;
} else {
return cur;
}
}
return null;
}
//查找当前节点的父节点
public TreeNode getParentNode(int val) {
TreeNode cur = root;
TreeNode parent = root;
while (cur != null) {
if (val < cur.val) {
parent = cur;
cur = cur.leftChild;
} else if (val > cur.val) {
parent = cur;
cur = cur.rightChild;
} else {
if (cur == root) {
return null;
} else {
return parent;
}
}
}
return null;
}
//查找树的最大值节点
public TreeNode findMax(TreeNode root) {
TreeNode cur = root;
while (cur != null) {
if (cur.rightChild != null) {
cur = cur.rightChild;
} else {
System.out.println("maxNode :" + cur.val);
return cur;
}
}
System.out.println("tree is null");
return null;
}
//查找树的最小值节点
public TreeNode findMin(TreeNode root) {
TreeNode cur = root;
while (cur != null) {
if (cur.leftChild != null) {
cur = cur.leftChild;
} else {
System.out.println("minNode: " + cur.val);
return cur;
}
}
System.out.println("tree is null");
return null;
}
//查找当前结点的右子树按照中序遍历获取的第一个结点
public TreeNode findInorderSuccessor(TreeNode node) {
TreeNode cur = node.rightChild;
while (cur != null) {
if (cur.leftChild != null) {
cur = cur.leftChild;
} else {
return cur;
}
}
return cur;
}
//删除指定值的结点(难)
public void deleteNode(int key) {
TreeNode keyNode = find(key);
TreeNode parent = getParentNode(key);
if (keyNode.leftChild == null) {
if (keyNode == root) {
root = keyNode.rightChild;
return;
} else if (keyNode == parent.leftChild) {
parent.leftChild = keyNode.rightChild;
} else {
parent.rightChild = keyNode.rightChild;
}
} else if (keyNode.rightChild == null) {
if (keyNode == root) {
root = keyNode.leftChild;
} else if (keyNode == parent.leftChild) {
parent.leftChild = keyNode.leftChild;
} else {
parent.rightChild = keyNode.leftChild;
}
} else {
TreeNode targetParent = keyNode;
TreeNode target = keyNode.rightChild;
while (target.leftChild != null) {
targetParent = target;
target = target.leftChild;
}
keyNode.val = target.val;
//把问题转化为删除左子树为空的节点
if (targetParent.leftChild == target) {
targetParent.leftChild = target.rightChild;
} else {
targetParent.rightChild = target.rightChild;
}
}
}
//中序遍历二叉搜索树的递归实现
public void inOrder(TreeNode node) {
if (node != null) {
inOrder(node.leftChild);
System.out.print(" " + node.val + " ");
inOrder(node.rightChild);
}
}
//中序遍历二叉搜索树的非递归实现
public void inOrderNormal(TreeNode node) {
TreeNode cur = root;
LinkedList<TreeNode> s = new LinkedList<>();
while (cur != null || !s.isEmpty()) {
while (cur != null) {
s.addFirst(cur);
cur = cur.leftChild;
}
if (!s.isEmpty()) {
cur = s.removeFirst();
System.out.print(" " + cur.val + " ");
cur = cur.rightChild;
}
}
}
//前序遍历二叉搜索树的递归实现
public void preOrder(TreeNode node) {
if (node != null) {
System.out.print(" " + node.val + " ");
preOrder(node.leftChild);
preOrder(node.rightChild);
}
}
//前序遍历二叉搜索树的非递归实现
public void preOrderNormal(TreeNode node) {
TreeNode cur = root;
LinkedList<TreeNode> s = new LinkedList<>();
while (cur != null || !s.isEmpty()) {
while (cur != null) {
System.out.print(" " + cur.val + " ");
s.addFirst(cur);
cur = cur.leftChild;
}
if (!s.isEmpty()) {
cur = s.removeFirst();
cur = cur.rightChild;
}
}
}
//后序遍历二叉搜索树的递归实现
public void postOrder(TreeNode node) {
if (node != null) {
postOrder(node.leftChild);
postOrder(node.rightChild);
System.out.print(" " + node.val + " ");
}
}
//后序遍历二叉搜索树的非递归实现
public void postOrderNormal(TreeNode node) {
TreeNode cur = root;
LinkedList<TreeNode> s1 = new LinkedList<>();
LinkedList<TreeNode> s2 = new LinkedList<>();
while (cur != null || !s1.isEmpty()) {
while (cur != null) {
s1.addFirst(cur);
s2.addFirst(cur);
cur = cur.rightChild;
}
if (!s1.isEmpty()) {
cur = s1.removeFirst();
cur = cur.leftChild;
}
}
while (!s2.isEmpty()) {
System.out.print(" " + s2.removeFirst().val + " ");
}
}
public static void main(String[] args) {
BinarySearchTree binarySearchTree = new BinarySearchTree(5);
binarySearchTree.insert(3);
binarySearchTree.insert(7);
binarySearchTree.insert(1);
binarySearchTree.insert(4);
binarySearchTree.insert(6);
binarySearchTree.insert(8);
binarySearchTree.insert(0);
binarySearchTree.insert(2);
binarySearchTree.insert(9);
System.out.println("------------递归实现--------------");
binarySearchTree.inOrder(binarySearchTree.root);
System.out.println();
binarySearchTree.preOrder(binarySearchTree.root);
System.out.println();
binarySearchTree.postOrder(binarySearchTree.root);
System.out.println();
System.out.println("------------非递归实现--------------");
binarySearchTree.inOrderNormal(binarySearchTree.root);
System.out.println();
binarySearchTree.preOrderNormal(binarySearchTree.root);
System.out.println();
binarySearchTree.postOrderNormal(binarySearchTree.root);
System.out.println();
System.out.println("查找指定节点:1");
TreeNode ret = new TreeNode(-1);
ret = binarySearchTree.find(1);
System.out.println("找到了: " + ret.val);
System.out.println("查找当前节点的父节点");
ret = binarySearchTree.getParentNode(3);
System.out.println("3节点的父节点是:" + ret.val);
System.out.println("查找最大值节点:");
ret = binarySearchTree.findMax(binarySearchTree.root);
System.out.println("查找最小值节点:");
ret = binarySearchTree.findMin(binarySearchTree.root);
System.out.println("查找当前结点的右子树按照中序遍历获取的第一个结点");
ret = binarySearchTree.findInorderSuccessor(binarySearchTree.root);
System.out.println(ret.val);
System.out.println("节点删除");
binarySearchTree.deleteNode(7);
binarySearchTree.inOrder(binarySearchTree.root);
}
}
3.应用场景
二叉搜索树作为一种经典的数据结构,它既有链表的快速插入与删除操作的特点,又有数组快速查找的优势;所以应用十分广泛,例如在文件系统和数据库系统一般会采用这种数据结构进行高效率的排序与检索操作
未完待续~