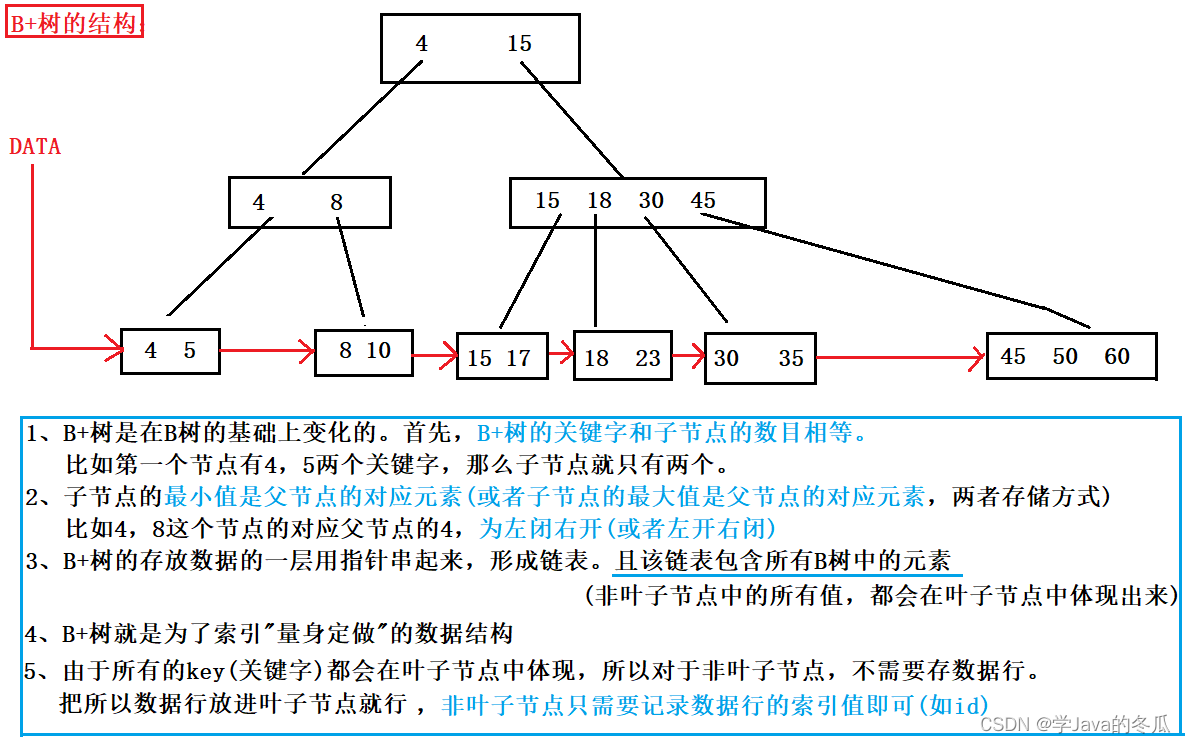
Q1 左孩子右兄弟

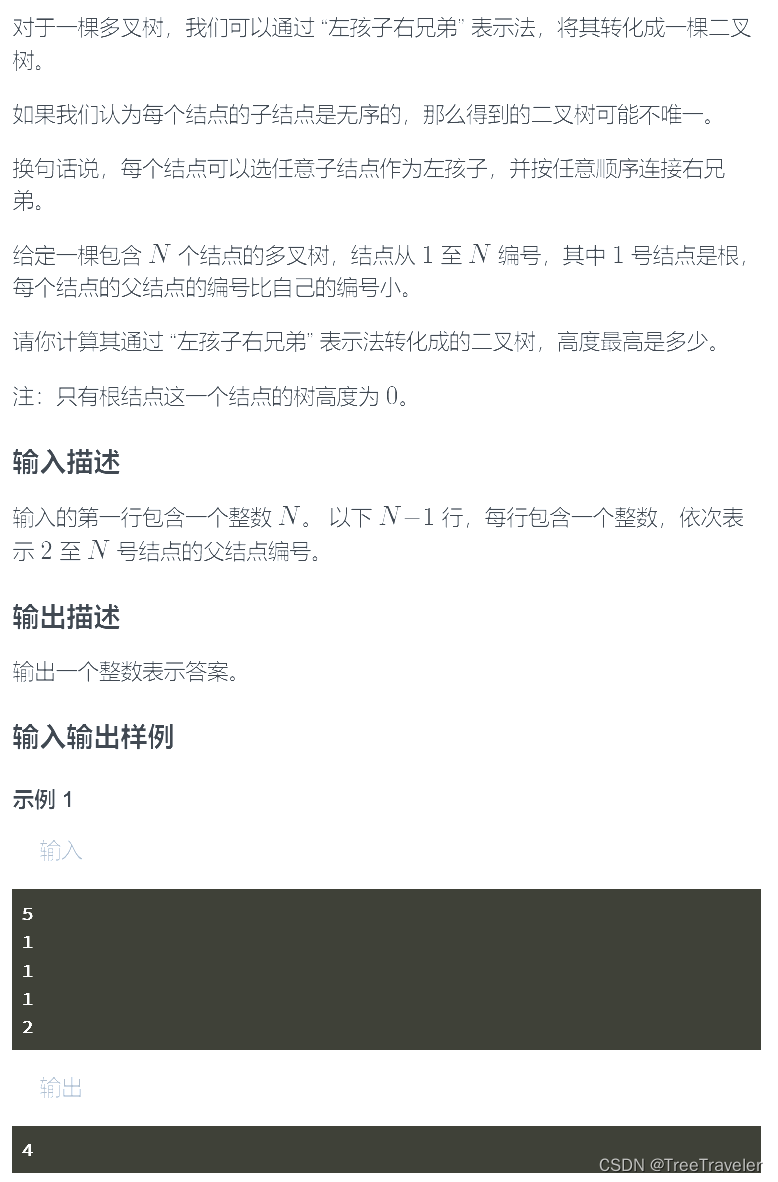
在这里插入图片描述

$f[u] 表示以u为根转化而成的二叉树（以下简称二叉树)的最大高度\\ f[u] = max(f[j_i]) + cnt[u] - 1 + 1, j_i是u\\的所有儿子，cnt[u]表示原树中u的儿子个数。因为\\ 以u为根的二叉树肯定由u的一个儿子为根的二叉树构成来作为他的左半部\\ 假设f[j_t]是最大的那个,那么u除去t的所有儿子应该可以被加到t为根的子\\ 树中作为兄弟，因为t为根的已经是二叉树，补充兄弟后一定是变高。\\$

/*
* @Author: gorsonpy
* @Date:   2022-12-19 10:36:45
* @Last Modified by:   gorsonpy
* @Last Modified time: 2022-12-19 10:45:57
*/
#include <iostream>
#include<cstring>
using namespace std;

const int N = 1e5 + 10;
int e[N], ne[N], h[N], idx;
int cnt[N], f[N];

void add(int a, int b)
{
  e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void dfs(int u, int fa) //计算以u为根的多叉树转化成二叉树后的最大高度
{
  for(int i = h[u]; ~i; i = ne[i])
  {
    int j = e[i];
    if(j == fa) continue;
    dfs(j, u);
    f[u] = max(f[u], f[j] + cnt[u]);
  } 
}
int main()
{
  memset(h, -1, sizeof h);
  int n;
  cin >> n;
  for(int i = 0; i < n - 1; ++i)
  {
    int x;
    cin >> x;
    add(x, i + 2);
    cnt[x] ++;
  }
  dfs(1, 0);
  cout << f[1] << endl;
  return 0;
}

Q2 作物杂交

在这里插入图片描述

正解应该是Spfa/BellmanFord(虽然官方给的tag是搜索？），题目不保证输入不会有A+B能杂交出多个种类的情况，也不保证某个种类只能由一种组合杂交而来，也不保证不会有相同输入。搜索可能成环。

$把种类抽象为图的点，每个合成方式理解为一条边，对于A+B可以合成\\ C，我们建立两条边，一个是A到C，边权为B，一个是B到C，边权为A。\\ 利用spfa的拓扑性质，判断每次合成一个种类时，他的子类是否已经得到\\过。最后的ans = f[t],t为所求终点品类。$

#include<iostream>
#include<queue>
#include<cstring>

using namespace std;
const int N = 1e5 + 10;

int d[N], h[N], e[2 * N], ne[2 * N], w[2 * N], idx;
int n, m, k, t;
int tim[N];
bool st[N], hav[N];

void add(int a, int b, int c) // a, b可以合成c
{
    e[idx] = c, ne[idx] = h[a], w[idx] = b, h[a] = idx++;
}

int spfa()
{
    memset(d, 0x3f, sizeof d);
    queue<int> q;
    for(int i = 1; i <= n; ++i)
    {
        if(hav[i])
        {
            q.push(i);
            st[i] = true;
            d[i] = 0;
        }
    }
    
    while(q.size())
    {
        int x = q.front();
        q.pop();
        st[x] = false;
        
        
        for(int i = h[x]; ~i; i = ne[i])
        {
            int z = e[i], y = w[i];
            if(hav[x] && hav[y])
            {
                hav[z] = true;
                int cost = max(d[x], d[y]) + max(tim[x], tim[y]);
                if(d[z] > cost)
                {
                    d[z] = cost;
                    if(!st[z])
                    {
                        q.push(z);
                        st[z] = true;
                    }
                }
            }
        }
    }
    
    return d[t];
}
int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m >> k >> t;
    for(int i = 1; i <= n; ++i) cin >> tim[i];
    for(int i = 1; i <= m; ++i)
    {
        int x;
        cin >> x;
        hav[x] = true;
    }
    
    for(int i = 1; i <= k; ++i)
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
        add(b, a, c);
    }
    
    cout << spfa() << endl;
    return 0;
}