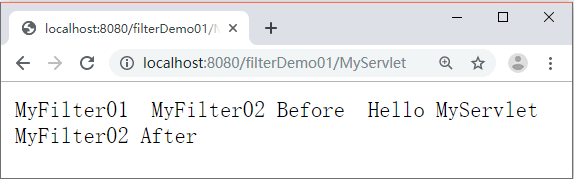
Prime Game - Gym 101981J - Virtual Judge (vjudge.net)

Problem - 1520 (nefu.edu.cn)

 解析：

这道题还是要考虑数的贡献

 题解参考至（【ACM-ICPC 2018 南京现场赛 】 J.Prime Game ---- 思维+素数筛_WangMeow的博客-CSDN博客）

第一个元素的素因子2：
它能贡献的区间有[1,1]，[1,2]，……，[1,10] 10个区间
第一个元素的素因子3：
它能贡献的区间有[1,1]，[1,2]，……，[1,10] 10个区间
当前sum = 10+10
第二个元素的素因子7：
它能贡献的区间有[1,2]，[1,3]，……，[1,10] 9个区间
它能贡献的区间有[2,2]，[2,3]，……，[2,10] 9个区间
当前sum = 10+10 +9*2
同理第三个元素的素因子5算好后 sum = 10+10+9*2+8*3
当考虑第四元素的素因子5时，发现i = 3时的素因子5
在区间:
[1,3]，[1,4]，……，[1,10]
[2,3]，[2,4]，……，[2,10]
[3,3]，[3,4]，……，[3,10]
这3*8个区间中已经贡献过，所以我们从当前i = 4位置向后考虑 这个位置的素因子5对区间的贡献为 7
sum = 10+10+9*2+8*3+7

最终到n = 10，sum = 10+10+9*2+8*3+7+6*4+5*5+4+0+2*4+1+3=134
依次向后推理，我们现在每个素因子i贡献公式为：

a n s i = ( n − p r i m e [ i ] [ p o s ] + 1 ) ∗ ( p r i m e [ i ] [ p o s ] − p r i m e [ i ] [ p o s − 1 ] ) ans_i = (n-prime[i][pos]+1)*(prime[i][pos]-prime[i][pos-1])ans 
i
​
 =(n−prime[i][pos]+1)∗(prime[i][pos]−prime[i][pos−1])
所以我们分解出质因子，把他们的位置放进vector, 扫一遍素数即可
————————————————
版权声明：本文为CSDN博主「WangMeow」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/m0_37624640/article/details/83276324

知道了大致思路后就是如何实现的问题了

我第一次写的代码时间复杂度稍微超过了2秒

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>

using namespace std;
typedef long long LL;
const int N = 1e6 + 5;

int n, mx = N - 1;
int arr[N], brr[N], vis[N];
vector<int>Prime;

void init() {
	for (int i = 2; i * i <= mx; i++) {
		if (arr[i] == 0)
			for (int j = i * i; j <= mx; j += i) {
				arr[j] = 1;
			}
	}
	for (int i = 2; i <= mx; i++) {
		if (arr[i] == 0)
			Prime.push_back(i);
	}
}

int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) {
		scanf("%d", &brr[i]);
	}
	init();
	LL ans = 0;
	for (int i = 1; i <= n; i++) {
		LL t1 = n - i + 1;
		for (int j = 0; j < Prime.size() && Prime[j] <= brr[i]; j++) {
			if (brr[i] % Prime[j] == 0) {
				LL t2 = i - vis[Prime[j]];
				ans += t1 * t2;
				vis[Prime[j]] = i;
			}
		}
	}
	cout << ans << endl;
	return 0;
}

注意看，实际上优化的空间还是蛮大的。

我的第二层循环中

for (int j = 0; j < Prime.size() && Prime[j] <= brr[i]; j++)

这里我们可以这么写

for (int j = 0; j < Prime.size() && Prime[j]*Prime[j] <= brr[i]; j++)

然后再循环内加上

while (brr[i] % Prime[j] == 0)brr[i] /= Prime[j];

直到最后跳出循环时，如果brr[i]>1，那么此时的brr[i]即是一个质数

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>

using namespace std;
typedef long long LL;
const int N = 1e6 + 5;

int n,mx=N-1;
int arr[N],brr[N],vis[N];
vector<int>Prime;

void init() {
	for (int i = 2; i <= mx; i++) {
		if (!arr[i]) {
			Prime.push_back(i);
		}
		for (int j = 0; j < Prime.size() && Prime[j] * i <= mx; j++) {
			arr[Prime[j] * i] = 1;
		}
	}
}

int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) {
		scanf("%d", &brr[i]);
	}
	init();
	LL ans = 0;
	for (int i = 1; i <= n; i++) {
		LL t1 = n - i + 1;
		for (int j = 0; j < Prime.size() && Prime[j]* Prime[j] <= brr[i]; j++) {
			if (brr[i] % Prime[j] == 0) {
				LL t2= i - vis[Prime[j]];
				while (brr[i] % Prime[j] == 0)brr[i] /= Prime[j];
				ans += t1 * t2;
				vis[Prime[j]] = i;
			}
		}
		if (brr[i] > 1) {
			LL t2 = i - vis[brr[i]];
			ans += t1 * t2;
			vis[brr[i]] = i;
		}
	}
	cout << ans << endl;
	return 0;
}