Trie的表现形式

Trie树主要用来实现字符串的存储和快速查找，其表现形式类似一颗多叉树，每个节点表示字符串的一个字符。由于可能会存在类似 "abc" 和 "abcde" 这样的数据，所以并不是只有叶子结点是字符串你的尾部，因此需要对每个字符串的尾部都进行标记。

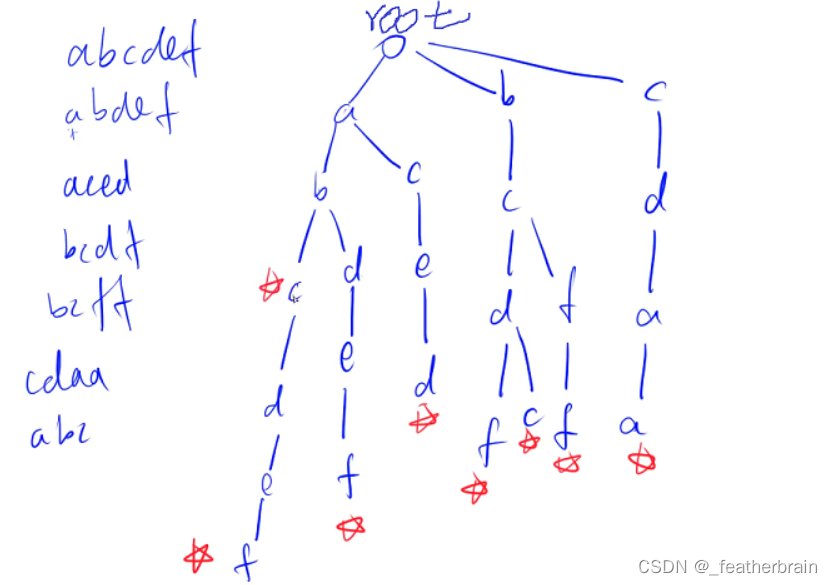
在这里插入图片描述

数组实现 Trie 树

提示：

初学的时候代码可能会看得云里雾里的，这是很正常的，因为很抽象，所以强烈建议通过画图来进行加深理解。最好先去了解一下数组实现链表

通过题目来实现Trie树

在这里插入图片描述

虽然Trie树的逻辑结构是一个多叉树，但是在实现的时候我们是通过数组的形式来进行存储的，所以物理结构可能会有点扭曲，可以类比一下数组实现链表时的操作。

题目给出的 N 表示的是所有字符串的长度之和，也就是节点总个数（不是树的高度）。每个节点都会有26种情况（对应着26个字母），所以我们开出的数组是 son[N][26]，它的一维表示的是当前节点位置，二维表示节点的值，里面存放的是下一个节点的位置。

字符串的结束需要标记，所以需要另外一个数组 cnt[N] 来进行存放。因为有 N 个节点，所以可能会有 N 中情况，所以需要开 N 个，它的下标表示最后节点的位置，里面存放的是以这个节点结束的字符串的个数

用图来表示就是：

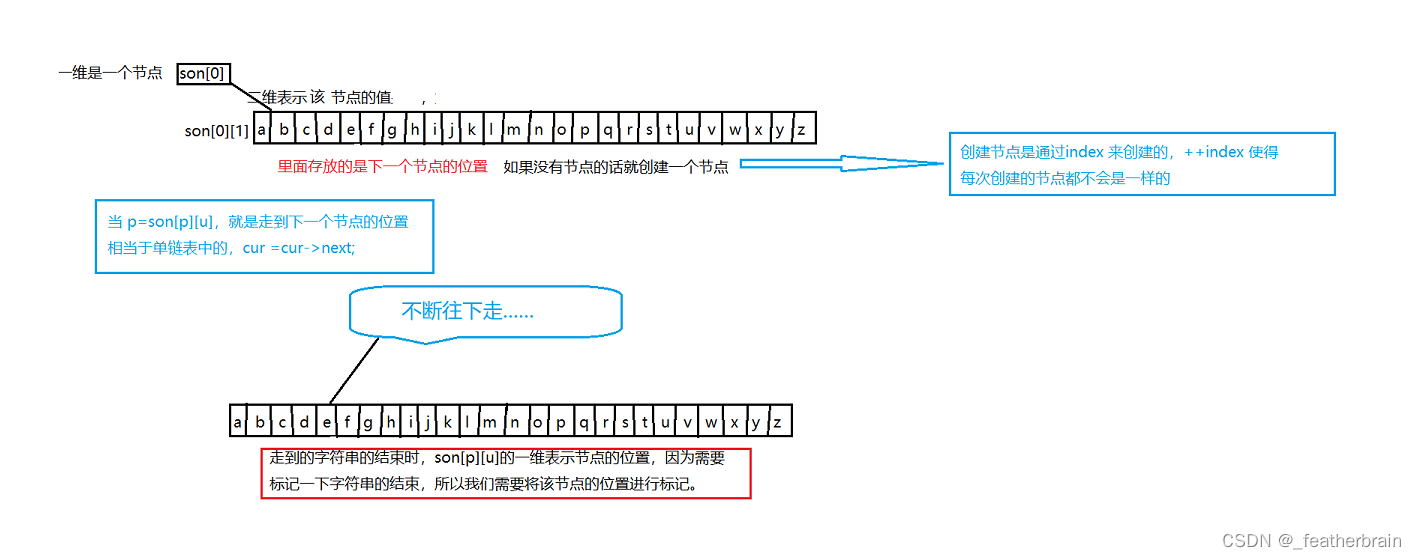
在这里插入图片描述

代码

#include <iostream>
#include <string>

using namespace std;

const int N = 100010;   // 表示的是所有的字符串加起来的长度
int son[N][26];      // son 表示下一个节点的位置，它的一维是表示当前节点的位置，二维表示当前节点的值
int cnt[N];          // cnt 表示一个字符串最后的标记位
int n, index;   // index 表示下一个用到的节点，让在不同字符串中的相同字符所在的位置不同
string s;
char str[N];

// 插入操作
void add(char str[])
{
    int p = 0;  // 一维表示的是节点，所以从0开始
    for (int i = 0; str[i]; i++)
    {
        int u = str[i] - 'a';   // 节点的值
        if (!son[p][u]) son[p][u] = ++index;    // 没有节点就创建节点
        p = son[p][u];   // 走到下一个节点
    }
    
    cnt[p]++;   // 标记字符串结束
}

// 查询操作
int query(char str[])
{
    int p = 0;  // 一维表示的是节点，所以从0开始
    for (int i = 0; str[i]; i++) 
    {
        int u = str[i] - 'a';   // 节点的值
        if (!son[p][u]) return 0;    // 如果节点不存在，说明没有这个字符串
        p = son[p][u];  // 走到下一个节点。
    }
    
    return cnt[p];  // 字符串的总个数
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; i++)
    {
        cin >> s >> str;
        if (s == "I") 
        {
            add(str);
        }
        else 
        {
            cout << query(str) << endl;
        }
    }
    
    return 0;
}