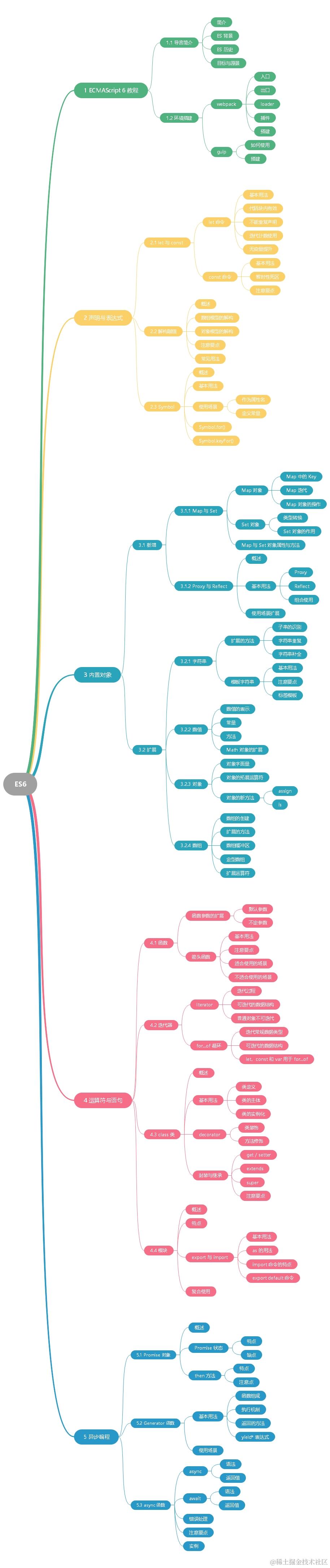
高精度算法出现的原因
当参与运算的
数的范围大大的超出了标准数据类型,如int(-2147483648 ~ 2147483647)或者long long的范围,就需要使用高精度算法来进行数的运算。高精度运算的特点是代码长度比较长,本质是对数学运算过程的模拟。既然不能使用标准数据类型,所以考虑使用字符串或者数组来存储这类大数据。
常用的一些最大值符号
0x7f7f7f7f—— 比int的最大值小一点0x3f3f3f3f—— 比int的最大值的一半小一点INT_MAX——int的最大值
#include <iostream>
#include <climits>
using namespace std;
int main()
{
cout << 0x7f7f7f7f << endl; //21 3906 2143
cout << 0x3f3f3f3f << endl; //10 6110 9567
cout << INT_MAX << endl; //21 4748 3647
return 0;
}
高精度加法分析
对于小数据,125 + 25 = 150,其运算过程如下:

由于涉及到进位,所以在计算机进行运算的时候,会采取倒序运算的方式。如果在运算时需要进位,则向下一位进位即可。

最后,需要倒序输出结果 :051,得到150,即最后的答案
高精度加法运算步骤:
- 使用字符数组存储两个较大的数
- 把两个数逆序转化为整数数组
- 诸位相加运算,在运算的时候处理进位。
- 相加之后的结果最多比原来较长的数多一位,最后逆序输出即可
高精度加法模板
待更新
高精度减法分析
在高精度减法中,需要注意:
- 如果
a < b,则需要先交换a与b,最后在输出结果前加上负号 - 在高精度计算时,如果
a[i] < b[i],则需要先向高位借一位
高精度减法模板
待更新
高精度乘法分析
在日常生活中,计算两个数字相乘,其过程是什么样子的呢?

通过上图,不难看出,1234 * 32 = 39488。那么,如何使用计算机来模拟上述的乘法运算过程是实现高精度乘法的核心所在。如果将数字全部转化为字符,那么上图过程则抽象为下图所示:

通过上图,不难发现下面的对应关系:('A —> B’表示A与B有关)
A[1] * B[1] ——> C[1]
A[2] * B[1] ——> C[2]
A[3] * B[1] ——> C[3]
A[4] * B[1] ——> C[4]
A[1] * B[2] ——> C[2]
A[2] * B[2] ——> C[3]
A[3] * B[2] ——> C[4]
A[4] * B[2] ——> C[5]
通过观察总结,发现下面规律:
A[i] * B[j] —> C[i + j - 1]
高精度算法核心代码:
c[i + j - 1] += (a[i] * b[j]);
c[i + j] += c[i + j - 1] / 10;
c[i + j - 1] %= 10;
最后需要注意的是,在高精度乘法中,得到的结果可能是多个0(如下图所示),所以删除前导0需要用while循环而不是if语句。

高精度乘法模板
待更新
高精度除法分析
高精度除法模板
待更新