引例
不知道你有没有玩过猜数字游戏,在0到100之间随机选取一个数,让你猜是几,比如这个数是67,如果你猜了50,就会提示你小了,那么你就会去51到100之间猜,你猜了75,就会提示你大了,你就会去51到74之间去猜,就这样一直猜,数字可取的区间越来越小,用不了多久就可以猜出.当你每次都将区间减半,就是二分了
二分的本质
对于二分查找的本质不是单调性,有单调性的题目必然可以二分,可以二分的题目不一定非得有单调性,例如上方引例就是有单调性.
那么二分的本质是什么呢?在一个区间中满足某种性质的元素都在右边,不满足的都在左边,就可以使用二分.每次二分都会将答案所在的要求的区间减少一半(注:这两个区间没有交界)

以下是二分的模版,先看过再理解
int bsearch_1(int l, int r)
{
int mid = (l + r) >> 1;
while (l < r)
{
if (check(mid)) // check()判断mid是否满足某种性质
{
r = mid;
}
else
{
l = mid + 1;
}
}
return 1;
}
int bsearch_2(int l, int r)
{
int mid = (l + r + 1) >> 1;
while (l < r)
{
if (check(mid)) // check()判断mid是否满足某种性质
{
l = mid;
}
else
{
r = mid - 1;
}
}
return 1;
}我们可以类比猜数字游戏
其中第一个模版就是判断你猜的数字是否小于x,如果为真,区间的r不变,l为你猜的那个数字加一,否则区间的l不变,r为你猜的那个数字
第二个模版就是判断你猜的数字是否大于x(x是选取的数),如果为真(大于x),区间的l不变,r为你猜的这个数字减一,否则区间的r不变,l为你猜的那个数字
数的范围(二分查找应用)
给定一个按照升序排列的长度为n的整数数组,以及 q 个查询。
对于每个查询,返回一个元素k的起始位置和终止位置(位置从0开始计数)。
如果数组中不存在该元素,则返回“-1 -1”。
输入格式
第一行包含整数n和q,表示数组长度和询问个数。
第二行包含n个整数(均在1~10000范围内),表示完整数组。
接下来q行,每行包含一个整数k,表示一个询问元素。
输出格式
共q行,每行包含两个整数,表示所求元素的起始位置和终止位置。
如果数组中不存在该元素,则返回“-1 -1”。
数据范围
1≤n≤1000001≤n≤100000
1≤q≤100001≤q≤10000
1≤k≤100001≤k≤10000
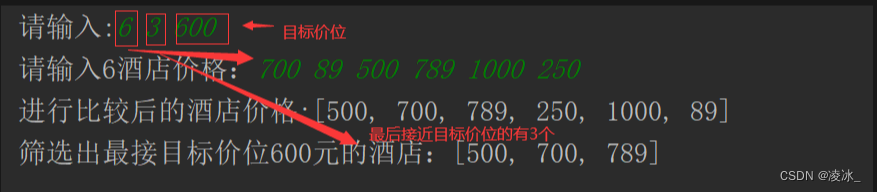
输入样例:
6 3
1 2 2 3 3 4
3
4
5
输出样例:
3 4
5 5
-1 -1
分析
我们来看这题怎么样可以将二分的知识套进去呢,首先处理的这个问题是单调递增的,所以一定可以使用二分查找,题目要求我们找到一个数字(可能有多个,也可能没有)在数组中的起始位置和终止位置,那么可以查找第一个大于等于这个数的位置,查找第一个小于等于这个数的位置,一般来说这个就是他的起始和终止位置,但是有可能这个数在数组中不存在,所以还得判断这个数是否与数组[起始位置]或者数组[终止位置]相等,如果不相等,则说明数组中不存在这个数
来人,上代码!
const int N = 100010;
int p[N];
int n;
int q; // q次询问
int k; // 询问元素
int main(void)
{
scanf("%d%d", &n, &q);
for (int i = 0; i < n; i++)
{
scanf("%d", &p[i]);
}
while (q--)
{
scanf("%d", &k);
int l = 0, r = n - 1;
while (l < r)
{
int mid = (l + r) / 2;
if (p[mid] >= k) // 找第一个大于等于k的数
{
r = mid;
}
else
{
l = mid + 1;
}
}
if (p[l] != k)
{
printf("-1 -1\n");
}
else
{
printf("%d ", l);
int l = 0, r = n - 1;
while (l < r) // 找第一个小于等于k的数
{
mid = (l + r + 1) / 2;
if (p[mid] <= k)
{
l = mid;
}
else
{
r = mid - 1;
}
}
printf("%d\n", r);
}
}
return 0;
}运行结果

完美运行,还有一件事,数组是单调递增的!! 题目已经说明了,在输入数据的时候别出错
边界问题
为啥在代码中,第二次循环中mid=(l+r+1)/2,而不是mid=(l+r)/2,因为这是整数除法,会向下取整,所以不加1的话求的是中间或者中间偏左的下标,加1则求的是中间或者中间偏右的下标,那具体有什么影响?当自己写代码的时候,你可以将错就错,看看写了mid=(l+r)/2会发生什么,当代码进行到l=r-1时,此时l和r的区间内只有两个数,mid求的是l的下标(中间偏左),如果满足条件,那么l会更新成mid,而mid就是l,所以会死循环,如果不满足条件,r会更新成mid-1,也就是l-1,可能数组中明明有元素满足,可是却不能得到正确的答案,现在你应该明白了第二次循环的mid为什么要加一
记住,每次你选取的区间一定要包含答案