目录
一、选择题
二、算法题
1、统计回文
2、连续最大和
一、选择题
1、

解析:
p1是一个字符数组,存储了"abcd",p2是一个字符指针,指向了"ABCD",str是一个字符数组,存储了"xyz"。strcat(p1 + 2, p2 + 1)表示将p1的第三个元素开始的字符串和p2的第二个元素开始的字符串连接起来,也就是将"cd"和"BCD"连接起来,得到"cdBCD"。这个结果会覆盖p1的原来的内容,所以p1变成了"abcdBCD"。strcpy(str + 2, strcat(p1 + 2, p2 + 1))表示将str的第三个元素开始的字符串替换为strcat(p1 + 2, p2 + 1)的结果,也就是将"z"替换为"cdBCD"。这个结果会覆盖str的原来的内容,所以str变成了"xybcdBCD"。
2、

解析:n是一个二维数组,有两行三列,每个元素都是int类型。p是一个指向三个int元素的数组的指针,也就是说,p可以指向n的每一行。p=n表示p指向n的第一行,也就是{10,20,30}。p[0][0]表示p指向的第一行的第一个元素,也就是10。*(p[0]+1)表示p指向的第一行的第二个元素,也就是20。这里,p[0]相当于n[0],也就是n的第一行的地址,加1表示偏移一个int大小,也就是4个字节。(*p)[2]表示p指向的第一行的第三个元素,也就是30。这里,*p相当于n[0],也就是n的第一行的地址,用[]表示下标运算符,也就是取第三个元素。答案为B。
3、

解析:预处理阶段是对源文件进行一些文本替换和宏展开,不涉及语法和语义的检查,所以不会发现函数未定义的错误。编译阶段是将源文件转换为目标文件,也就是机器码的形式,这个阶段会检查语法和一些语义错误,但是不会检查函数是否定义,只要有函数的声明就可以通过编译。链接阶段是将多个目标文件和库文件合并为一个可执行文件,这个阶段会检查函数是否有定义,如果没有定义,就会报错,提示找不到函数的符号。执行阶段是运行可执行文件,这个阶段已经不会发现函数未定义的错误,因为如果有这样的错误,程序就无法生成可执行文件。
二、算法题
1、统计回文
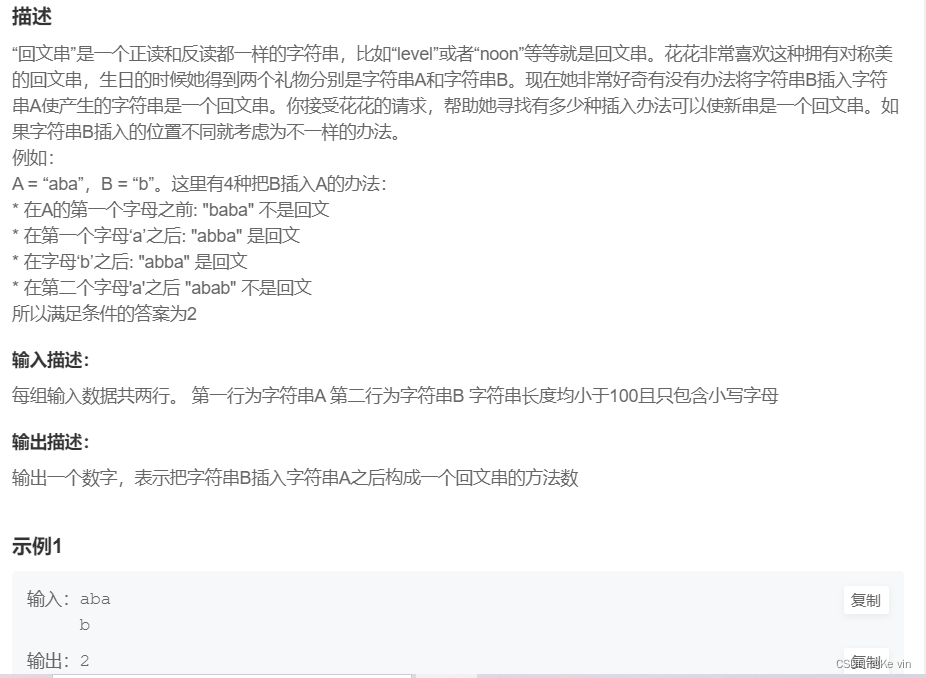
题目解析:本题使用暴力求解方式计算即可,遍历str1,将str2 insert进入str1的每个位置,判断是否是回文,是就++count;需要注意的是这里不能 str1.insert(i, str2),这样的话str1改变了,判断下一个位置就不对了。所以每次使用str1拷贝构造一个str,然后str.insert(i, str2),再判断。
#include <iostream>
#include<string>
using namespace std;
bool count( const string& str) {
size_t begin = 0;
size_t end = str.size() - 1;
while (begin < end) {
if (str[begin] != str[end]) {
return false;
} else {
begin++;
end--;
}
}
return true;
}
int main() {
string A, B;
getline(cin, A);
getline(cin, B);
string newstr;
int num = 0;
for (int i = 0; i < A.size() + 1; i++) {
newstr = A;
newstr.insert(i, B);
if (count(newstr)) {
num++;
}
}
cout << num << endl;
}2、连续最大和

题目解析:本题是一个经典的动规问题,简称dp问题,但是不要害怕,这个问题是非常简单的dp问题。
状态方程式: max( dp[ i ] ) = getMax( max( dp[ i -1 ] ) + arr[ i ] ,arr[ i ] )dp[[i]是以i结尾的连续最大和,就相当于我们从开始一直往后加,每次相加之前都要把dp[i-1]+arr[i]和第i个数相比,看看前面i-1个数是否拖了后腿。取大的那个作为dp[i]。
#include <iostream>
#include<vector>
using namespace std;
int Maxnum(int sum,int a)
{
return sum>a?sum:a;
}
int main() {
int n=0;
cin>>n;
vector<int> arr;
arr.resize(n);
for(int i=0;i<n;i++)
{
cin>>arr[i];
}
int Sum=arr[0];
int Max=arr[0];
for(int i=1;i<n;i++)
{
Sum=Maxnum(Sum+arr[i],arr[i]);
if(Sum>Max)
{
Max=Sum;
}
}
cout<<Max<<endl;
}