博主主页:Yu·仙笙
专栏地址:洛谷千题详解
目录
题目描述
输入格式
输出格式
输入输出样例
解析:
C++源码:
C++源码2:
--------------------------------------------------------------------------------------------------------------------------------
 --------------------------------------------------------------------------------------------------------------------------------
--------------------------------------------------------------------------------------------------------------------------------
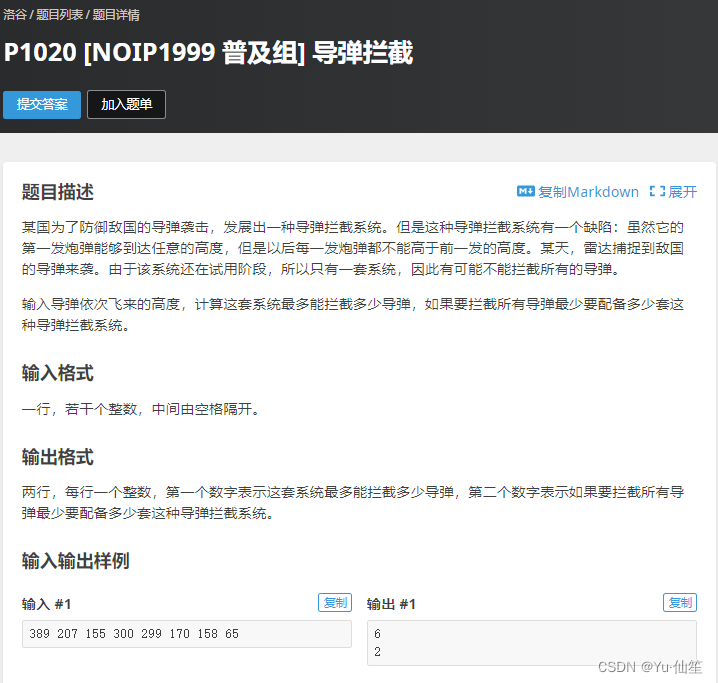
题目描述
某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。某天,雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。
输入导弹依次飞来的高度,计算这套系统最多能拦截多少导弹,如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
--------------------------------------------------------------------------------------------------------------------------------
输入格式
一行,若干个整数,中间由空格隔开。
--------------------------------------------------------------------------------------------------------------------------------
输出格式
两行,每行一个整数,第一个数字表示这套系统最多能拦截多少导弹,第二个数字表示如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
--------------------------------------------------------------------------------------------------------------------------------
输入输出样例
输入 #1
389 207 155 300 299 170 158 65
输出 #1
6 2
--------------------------------------------------------------------------------------------------------------------------------
解析:
将拦截的导弹的高度提出来成为原高度序列的一个子序列,根据题意这个子序列中的元素是单调不增的(即后一项总是不大于前一项),我们称为单调不升子序列。本问所求能拦截到的最多的导弹,即求最长的单调不升子序列。
考虑记 dpi 表示「对于前 i 个数,在选择第 ii 个数的情况下,得到的单调不升子序列的长度最长是多少」。于是可以分两种情况:
- 第 i 个数是子序列的第一项。则 1dpi←1。
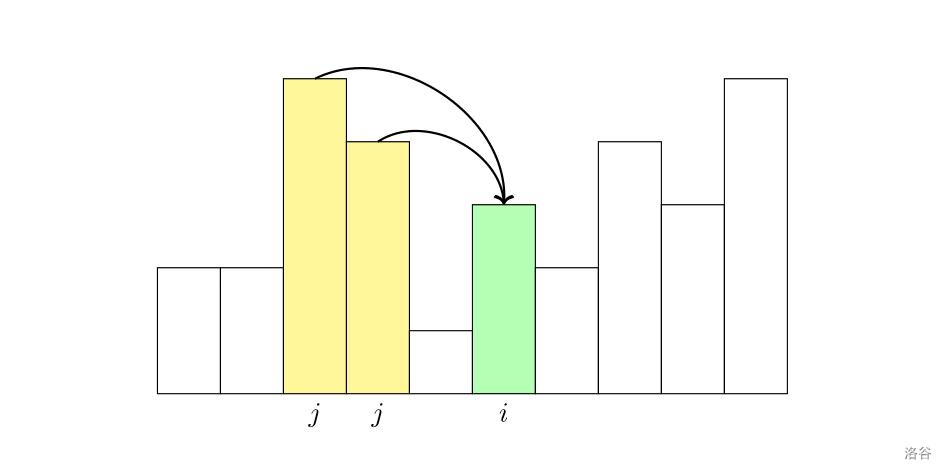
- 第 i 个数不是子序列的第一项。选择的第 i个数之前选择了第 j个数。根据题意,第 j 个数的值h(j) 应当小于第 i 个数的值 h(i)。枚举这样的 j,可以得到状态转移方程:
dpi=j<i,h(j)≥h(i)max{dpj+1}
综合这两种情况,得到最终的状态转移方程:
dpi=max{1,j<i,h(j)≥h(i)max{dpj+1}}
值得注意的是,第 n 个数不一定是最长单调不升子序列的最后一项。为了求出答案,我们需要枚举最后一项是哪个:
ans=1≤i≤nmax{dpi}
直接枚举进行状态转移,时间复杂度显然是O(n^2)。 下面考虑优化。
记 f_i表示「对于所有长度为 i 的单调不升子序列,它的最后一项的大小」的最大值。特别地,若不存在则 f_i=0。下面证明:
- 随 i 增大,f_i 单调不增。即fi≥fi+1。
考虑使用反证法。假设存在 u<v,满足 fu<fv。考虑长度为 v 的单调不升子序列,根据定义它以 f_v 结尾。显然我们可以从该序列中挑选出一个长度为 u 的单调不升子序列,它的结尾同样是 f_v。那么由于 fv>fu,与 f_u 最大相矛盾,得出矛盾。
因此 f_i 应该是单调不增的。
现在考虑以i 结尾的单调不升子序列的长度的最大值_idpi。由于我们需要计算所有满足 h(j)>h(i) 的 jj 中,jdpj 的最大值,不妨考虑这个jdpj 的值是啥。设j=xdpj=x,那么如果 h(i)> f_xh(i)>fx,由于 f_x\ge h(j)fx≥h(j),就有 h(i)>h(j)h(i)>h(j),矛盾,因此总有 h(i)\le f_xh(i)≤fx。
根据刚刚得出的结论,f_ifi 单调不增,因此我们要找到尽可能大的 x 满足 h(i)≤fx。考虑二分。

绿色区域表示合法的 f_xfx(即 f_x\ge h(i)fx≥h(i)),红色区域表示不合法的 f_xfx(即 f_x< h(i)fx<h(i)),我们需要找到红绿之间的交界点。
假设二分区域为 [l,r)[l,r)(注意开闭区间。图上黄色区域标出来了二分区域内实际有效的元素)。每次取 m=\frac{l+r}{2}m=2l+r,如果 f_mfm 在绿色区域内,我们就把 ll 移动到此处(l\gets ml←m);否则把 rr 移动到此处(r\gets mr←m)。
当 r-l=1r−l=1 时,ll 处位置即为我们需要找的位置。转移 \mathit{dp}_i\gets l+1dpi←l+1 即可。记得更新 ff。但是我们只用更新 f_{\mathit{dp}_i}fdpi,这是因为 f_1,f_2,\cdots f_{\mathit{dp_i}-1}f1,f2,⋯fdpi−1 的大小肯定都是不小于 h(i)h(i) 的。f_{\mathit{dp}_i}fdpi 是最后一个不小于 h(i)h(i) 的位置,f_{\mathit{dp}_i+1}fdpi+1 则小于 h(i)h(i)。
时间复杂度 \mathcal O(n\log n)O(nlogn),可以通过该问。
第二问
考虑贪心。
从左到右依次枚举每个导弹。假设现在有若干个导弹拦截系统可以拦截它,那么我们肯定选择这些系统当中位置最低的那一个。如果不存在任何一个导弹拦截系统可以拦截它,那我们只能新加一个系统了。
假设枚举到第 ii 个导弹时,有 mm 个系统。我们把这些系统的高度按照从小到大排列,依次记为 g_1,g_2,\cdots g_mg1,g2,⋯gm。容易发现我们就是要找到最小的 g_xgx 满足 g_x\ge h_igx≥hi(与第一问相同,这是可以二分得到的),然后更新 g_xgx 的值。更新之后,g_1,g_2\cdots g_xg1,g2⋯gx 显然还是单调不增的,因此不用重新排序;如果找不到符合要求的导弹拦截系统,那就说明 g_m<h_igm<hi,直接在后头增加一个就行。
时间复杂度 \mathcal O(n\log n)O(nlogn),可以通过该问。
--------------------------------------------------------------------------------------------------------------------------------
C++源码:
#include<bits/stdc++.h>
#define up(l,r,i) for(int i=l,END##i=r;i<=END##i;++i)
#define dn(r,l,i) for(int i=r,END##i=l;i>=END##i;--i)
using namespace std;
typedef long long i64;
const int INF =2147483647;
const int MAXN=1e5+3;
int n,t,H[MAXN],F[MAXN];
int main(){
while(~scanf("%d",&H[++n])); --n;
t=0,memset(F,0,sizeof(F)),F[0]=INF;
up(1,n,i){
int l=0,r=t+1; while(r-l>1){
int m=l+(r-l)/2;
if(F[m]>=H[i]) l=m; else r=m;
}
int x=l+1; // dp[i]
if(x>t) t=x; F[x]=H[i];
}
printf("%d\n",t);
t=0,memset(F,0,sizeof(F)),F[0]=0;
up(1,n,i){
int l=0,r=t+1; while(r-l>1){
int m=l+(r-l)/2;
if(F[m]<H[i]) l=m; else r=m;
}
int x=l+1;
if(x>t) t=x; F[x]=H[i];
}
printf("%d\n",t);
return 0;
}--------------------------------------------------------------------------------------------------------------------------------
C++源码2:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define maxn 1000010
using namespace std;
typedef long long ll;
ll a[maxn],n=1,dp1[maxn],dp2[maxn],len1,len2;
inline void write(ll x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
int main(){
while(cin>>a[n]){
n++;
}
n--,len1=1,len2=1;
dp1[1]=a[1],dp2[1]=a[1];
for(ll i=2;i<=n;i++){
if(a[i]<=dp1[len1]){
dp1[++len1]=a[i];
}
else{
ll k1=upper_bound(dp1+1,dp1+len1+1,a[i],greater<ll>())-dp1;
dp1[k1]=a[i];
}
if(a[i]>dp2[len2]){
dp2[++len2]=a[i];
}
else{
ll k2=lower_bound(dp2+1,dp2+len2+1,a[i])-dp2;
dp2[k2]=a[i];
}
}
write(len1);
puts("");
write(len2);
return 0;
}