本文中的所有重要图片都会给出基于Matplotlib的Python绘制代码以供参考

引言

请添加图片描述

如果在百度搜索圆角矩形的画法，那么多数结果都会告诉你，就是把一个普通矩形的拐角换成相切的 $\frac{1}{4}$ 圆弧，就像 引文1 和 引文2 说的那样。然而，圆角就是圆弧加直线吗？诸君且看下面这张图片，试问哪条曲线更顺滑、圆角更圆润？
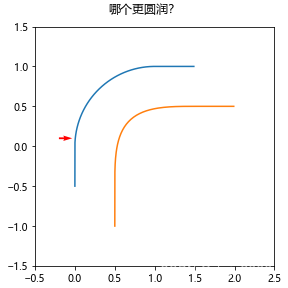
请添加图片描述
毫无疑问是黄线更顺滑一些，蓝线的转角在和直线的连接处（红色箭头）有种折断的感觉。如果我告诉你，蓝线就是 $\frac{1}{4}$ 圆弧和直线连接得到的，你会不会感觉很奇怪：明明连切线都对上了，怎么还会有折断感？

那么，这两条曲线的差别在哪里呢？答：黄线是二阶连续的，而蓝线仅仅是一阶连续。

二阶连续性

为了理解这里“二阶连续”的含义，首先要具备一个基础知识：如何表达和绘制二维平面上的曲线？

相信这篇文章的绝大多数读者都知道函数和函数图像的关系——我们可以使用函数来表达曲线。但是，我们不能用形如 $y = f (x)$ 这样的函数，因为函数是一个单射，如果使用这样的函数，那么在表达会绕回来的曲线时就会有困难，因为这时横坐标 $x$ 对应了两个 $y$ 值：

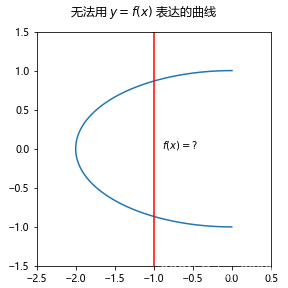
请添加图片描述
对于一般的情况，我们可以使用 $x$ 和 $y$ 间的隐函数来表达，引入一个隐变量 $t$ 就行了： $\left\{\begin{array}{cc} x = f_x(t) \\ y = f_y(t) \end{array}\right.$ 。如果把 $t$ 理解为时间，那么这个方程组实际上就描述了曲线的画法：对应任意的时间点 $t$ ，方程组给出了要绘制的点 $\left<x,\ y\right>$ 。

有了这个基础知识之后，就可以理解“二阶连续”了，这里的“二阶”则是指这 $f_x$ 和 $f_y$ 的二阶导，“连续”就是 $f_x''$ 和 $f_y''$ 连续的意思。那么问题来了：为什么偏偏要“二阶”呢？

二阶连续的物理含义

“二阶”的要求可以追溯到物理意义上。让我们回忆一下，在物理学中，速度是位置关于时间的导数： $\vec{v} = \frac{\mathrm{d}\vec{x}}{\mathrm{d}t}$ ，加速度是速度关于时间的导数： $\vec{a} = \frac{\mathrm{d}\vec{v}}{\mathrm{d}t}$ ，所以加速度是位置关于时间的二阶导数： $\vec{a} = \frac{\mathrm{d}^2\vec{x}}{{\mathrm{d}t}^2}$ ；物体的加速度不是凭空而来，而是由受力决定： $\vec{a} = \frac{\vec{F}}{m}$ ，加速度与物体的受力情况直接关联。

在这个模型中，由于在任意时刻位置都要满足二阶可导，因此物体的位置和速度都是不能突变的，也就是说，如下的两种运动都是不可能发生的：
请添加图片描述
而加速度就可以突变了，因为物体的受力可能发生突变，比如两个物体发生了碰撞——事实上，如果不考虑外力，碰撞就是系统内物体加速度突变的充要条件。

现在回到圆角矩形的绘制，让我们想象自己用手抚摸过圆角，这就将曲线的绘制和上面的物理模型联系了起来：
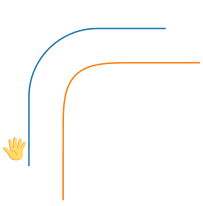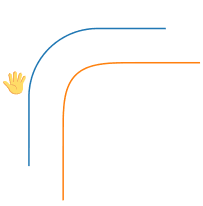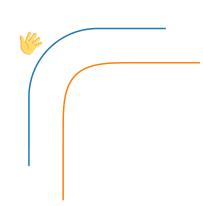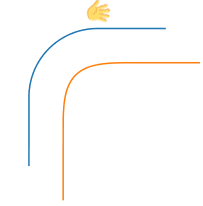
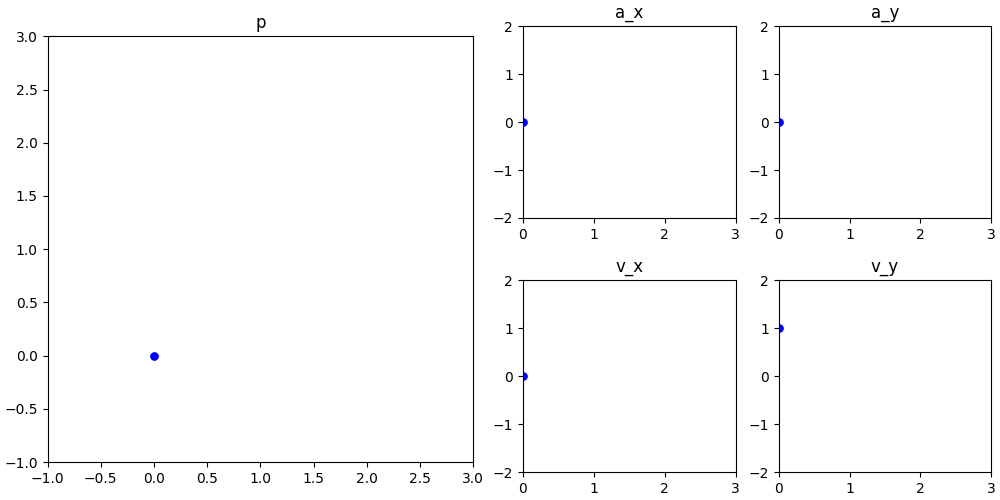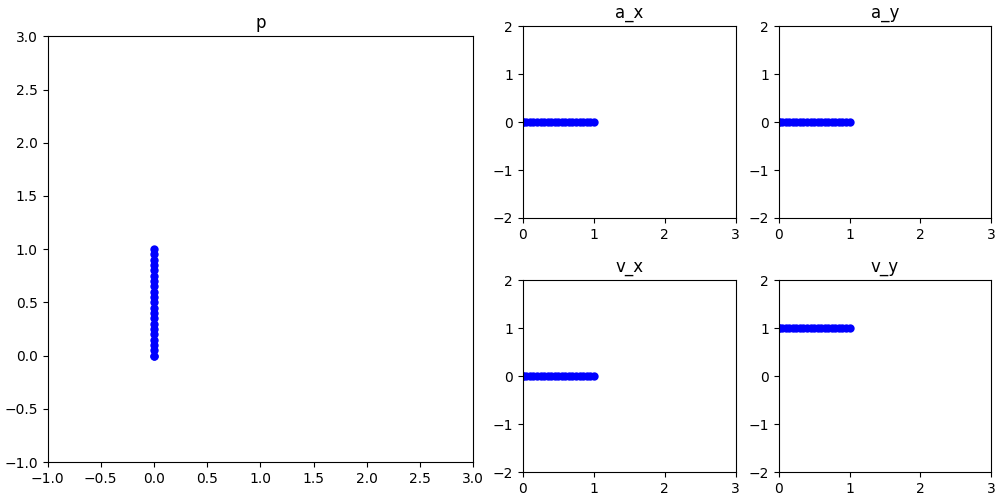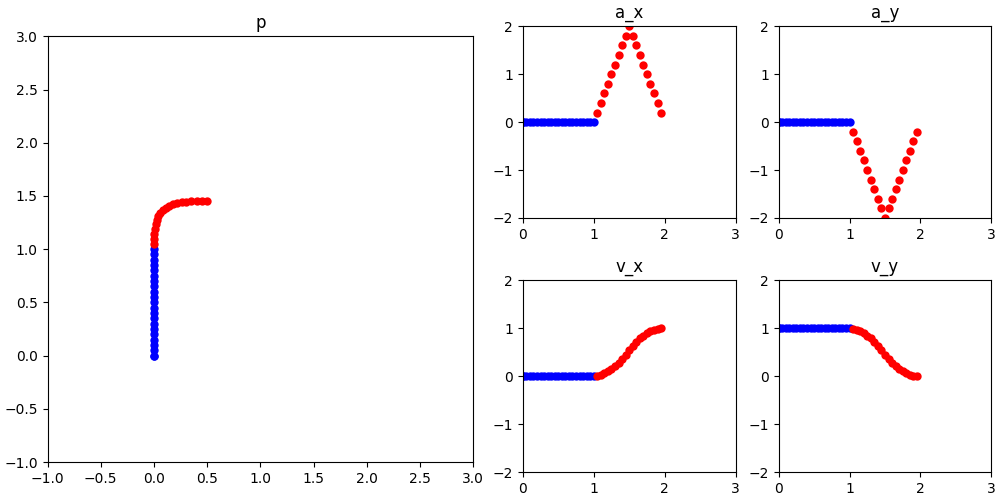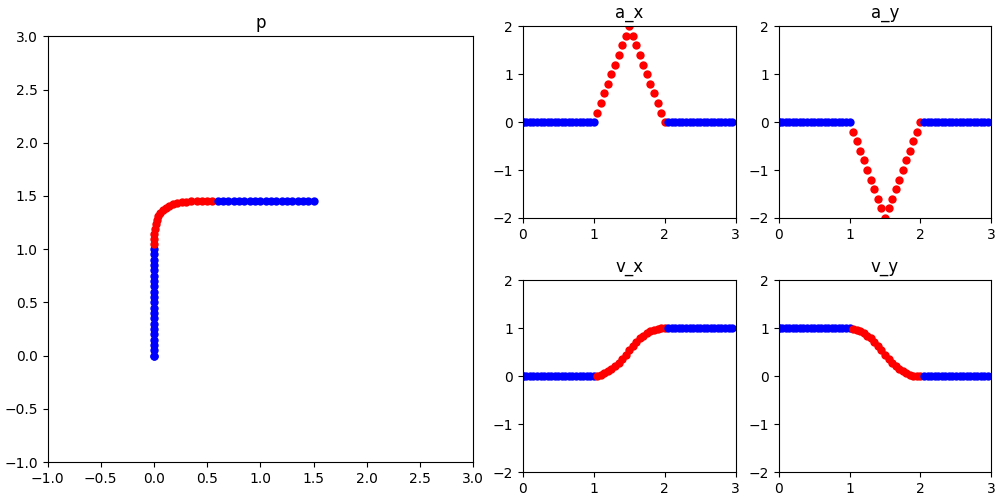
请添加图片描述
如果曲线不是二阶连续的，那么当手沿着曲线的轨迹运动时，在间断点处二阶导数发生突变，就意味着手就会突然受力，好像撞上了什么东西，因此我们就会感觉到“硌手”。下面这张动图绘制了沿圆弧+直线的轨迹的运动参数变化，可以直观地看到加速度的突变：

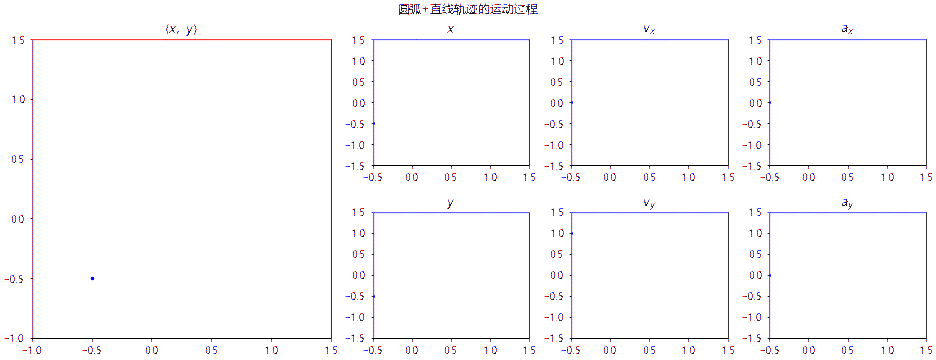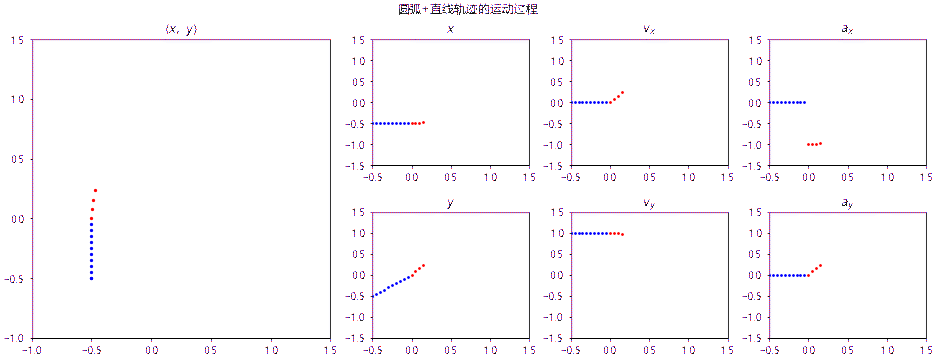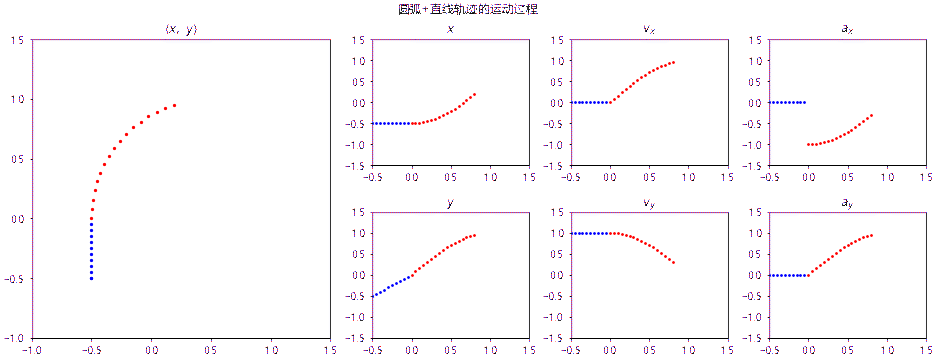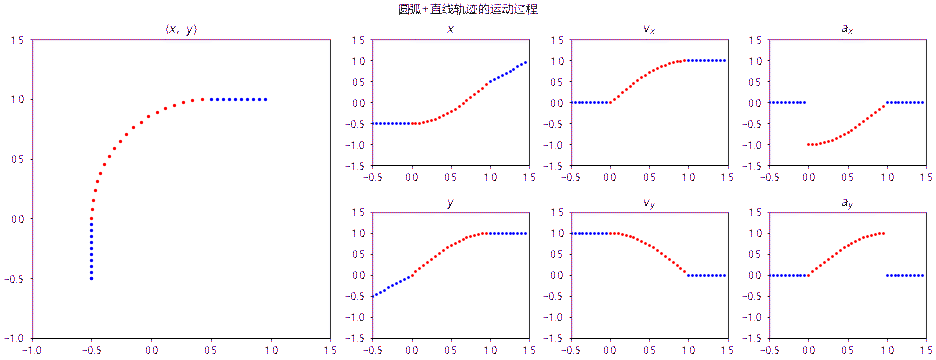
请添加图片描述

设计圆角曲线的函数

有了物理上的运动模型后，我们的思维就不再局限于圆和直线，从而可以重新设计圆角曲线的函数了。我们还是以左上角的圆角为例，目标是设计这样一组函数： $\left\{\begin{array}{l} x = f_x(t) \\ y = f_y(t) \end{array}\right.$ ，使得其满足：

$\left\{ \begin{aligned} & f_x(0) = 0,\ f_y(0) = 0 & (起点) \\ & f_x(1) = 1,\ f_y(1) = 1 & (终点) \\ & f_x'(0) = 0,\ f_y'(0) = 1 & (起始速度) \\ & f_x'(1) = 1,\ f_y'(1) = 0 & (终末速度) \\ & f_x''(0) = f_y''(0) = f_x''(1) = f_y''(1) = 0 & (与直线的连接点二阶连续) \\ & f_x'',\ f_y'' \in C[0,\ 1] & (加速度在闭区间[0,1]上连续) \\ & \forall t \in [0, 1] \left\{ \begin{aligned} & \frac{f_x(t) + f_x(1-t)}{2} + \frac{f_y(t) + f_y(1-t)}{2} = 1 \\ & f_y(1-t) - f_y(t) = f_x(1-t) - f_x(t) \end{aligned} \right. & (关于对角线对称) \end{aligned} \right.$

满足要求的函数当然不止一条，事实上，我们有很大的设计空间，那么，怎么从中找一条出来呢？

我们从二阶导数，也就是加速度函数入手，在设计出加速度函数后，只需要求解不定积分，就可以轻松满足前四项约束了。为此，我们首先分析上述约束对加速度函数的要求：

速度约束

$f_x'(1) - f_x'(0) = \int_0^1 f_x''(t)\ \mathrm dt = 1\\ f_y'(1) - f_y'(0) = \int_0^1 f_y''(t)\ \mathrm dt = -1$
对称约束

我们希望画出的圆弧是关于拐角的平分线 $x + y = 1$ 对称的，更进一步地，我们不光希望最终轨迹是对称的，最好绘制过程也是关于这条直线对称的，也就是说：

$\left\{ \begin{aligned} & f_y(1-t) = 1 - f_x(t) \\ & f_x(1-t) = 1 - f_y(t) \end{aligned} \right.$

上面的两个公式其实说了同一件事： $f_y(t) = 1 - f_x(1-t)$ ，这意味着我们在设计时只需设计 $f_x''$ 即可， $f_y''$ 可以直接由此求出来。

现在，问题已经很简单了：设计 $f_x''(t)$ 使它在 $0$ 和 $1$ 处为 $0$ ，并且在 $[0, 1]$ 上的积分为 $1$ 。

这样的函数还不好找吗？一个最简单的函数就是画个三角形：

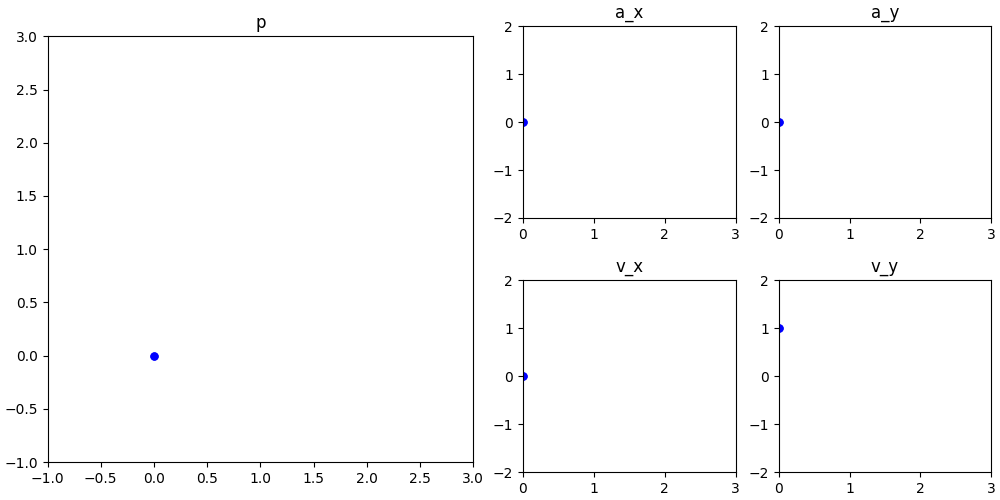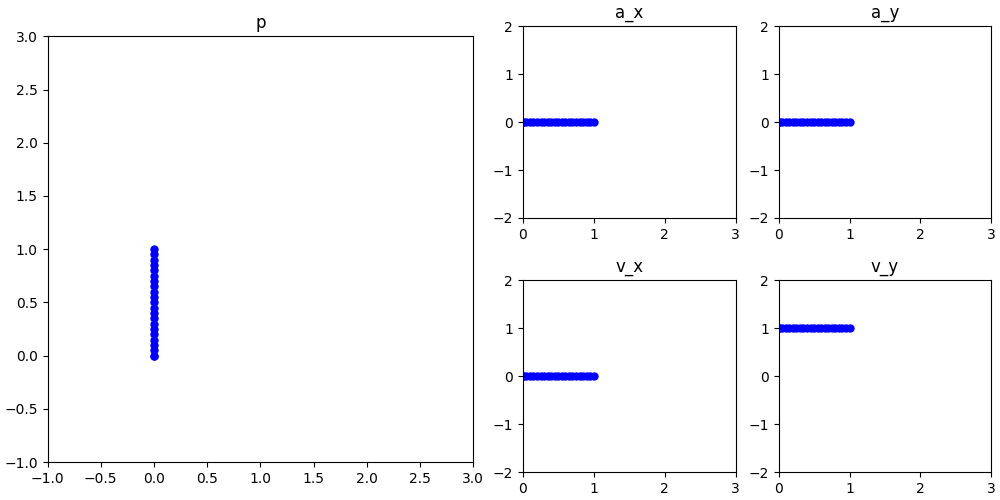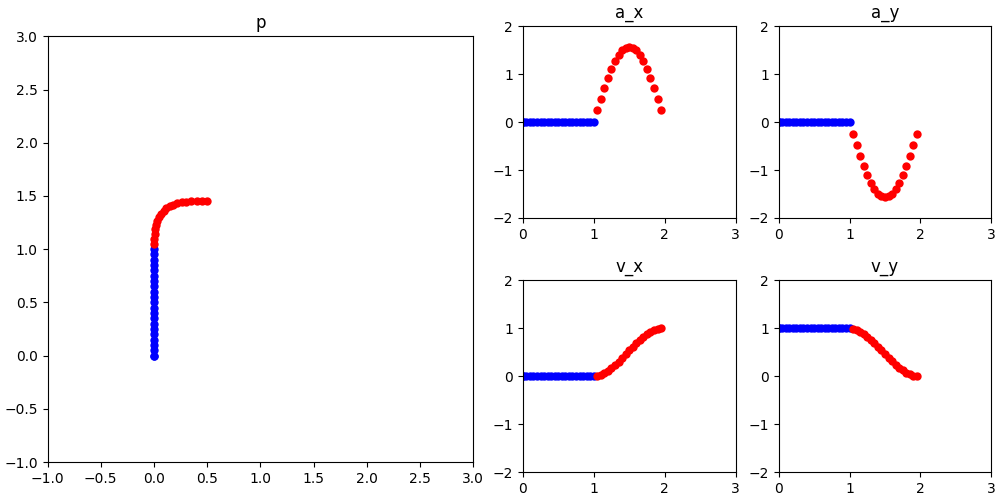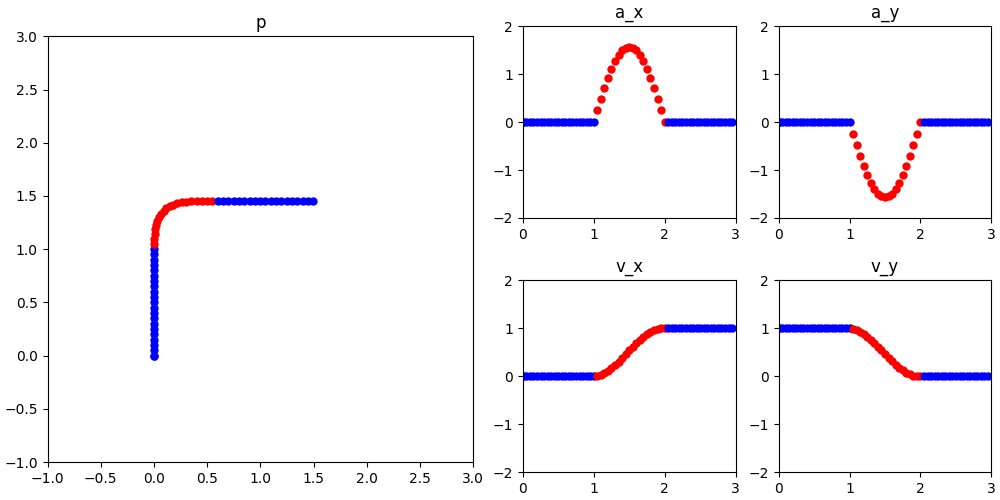
请添加图片描述也可以用正弦函数，更丝滑：

请添加图片描述

进一步探讨

匀速约束

如果运动的过程是匀速的，那么就意味着我们在绘制曲线时在相同的长度上花费了相同的时间，如果我们画的是虚线而非实线，那么虚线点之间的距离就是均匀的。另一方面，从性能的角度来看，这也很重要，因为我们只关心绘制的最终结果，而不关心过程，如果不均匀，那么就意味着我们绘制的开销和曲线的直观长度不符，这可能会限制我们绘制很长的曲线。

但其实这是一个伪约束，因为我们总可以通过一个后期处理得到一个均匀化的新解析式。在现实中的直观理解就是，施工队可能花了很多时间找到一条从A到B的路线，然而一旦路修好之后，我们总可以按自己喜欢的速度将这段路走完。在数学上，这就是对原运动过程进行时间上的放缩：

给定轨迹描述函数 $\left\{\begin{array}{cc} x = f_x(t) \\ y = f_y(t) \end{array}\right.$ ，我们总可以通过设计一个时间放缩函数 $s$ ，使得新轨迹函数 $\left\{\begin{array}{cc} x = f_x(s(t)) \\ y = f_y(s(t)) \end{array}\right.$ 满足 $\sqrt{(\frac{\mathrm{d}x}{\mathrm{d}t})^2 +(\frac{\mathrm{d}y}{\mathrm{d}t})^2 } = C$ ，其中 $C$ 为任意设定的速度常数。

要想求出这个 $s$ 函数，只需要解一个和原轨迹函数相关的微分方程即可，具体过程就不赘述啦！
高阶连续

从最开始的对比图上，我们可以得知，人眼是能分辨一阶连续和二阶连续的区别的，那么肯定有人就会问了：是不是更高阶的更丝滑？如果是，那么能不能做到在连接点处无穷阶连续，不就达到极致丝滑了吗？

其实设计一个高阶连续的函数并不是什么难事，事实上，我们可以用多项式凑出任意高阶的函数 $\sum_{i=0}^N a_i t^i$ ，假设目标为 $k$ 阶连续，则为了求出 $f_x''$ 可构建方程组：

$\left\{ \begin{aligned} & \int_0^1 P(t) \mathrm{\ d}t = 1 \\ & P^{(m)}(0) = 0 & \forall m \in [0, k] \\ & P^{(m)}(1) = 0 & \forall m \in [0, k] \end{aligned} \right.$

由 $P (t)$ 是 $N$ 阶多项式可以得出：
$\int_0^1 P(t) \mathrm{\ d}t = \sum_{i=0}^N \frac{a_i}{i+1} \\ P^m(t) = \sum_{i=m}^N \left( a_i \cdot \frac{i!}{(i-m)!} \cdot t^{i-m} \right)$

可见前面的方程组实际上是线性方程组，组中共 $2 k + 3$ 个方程，因此 $P (t)$ 必须要至少为 $2 k + 2$ 阶多项式才能得到实数解。

使用上面的方法，我绘制出了 $f_x''$ 0~11阶连续对应的曲线：

除了弧变得越来越小了之外，我个人觉得，这些曲线在连接处的顺滑度上看不出什么区别。这也许说明，经过漫长的自然演化后，人类的肉眼恰好进化到了能识别出有危险的二阶不连续拐角，而对高阶不连续就不敏感了。

现在，我们讨论第二个问题：能不能做到无穷阶连续？答案是不能的，因为如果无穷阶连续，就是在连接点处的无穷阶导数都为零，那么根据泰勒展开式，这条曲线就是 $\equiv 0$ ……，那就不可能拐弯了。也许，从另一方面来说，直线就是极致顺滑的曲线。

总结

本文系统讨论了圆角曲线的绘制方法，不仅给出了其数学解析式，更介绍了解析式的设计方法，最后本文通过绘制更高阶的连续曲线，证明了人类肉眼具备且仅具备区分二阶连续曲线的能力（不过也许有眼力好的人能看出最后一张图片曲线的差别）。本文所介绍的方法不仅适用于绘制 90° 拐角的曲线，稍加修改可以实现在任意两条线的断点处绘制任意阶连续的曲线。

附录

文中所有函数图片的绘制代码（按出现顺序给出）：

# %%
from math import cos, pi, sin, factorial
from timeit import repeat
from tkinter import Y

import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation

mpl.rcParams["font.family"] = "Microsoft YaHei"


# %%
fig, ax = plt.subplots(1, 1, layout="constrained")
fig.suptitle("哪个更圆润？")
fig.set_size_inches(4, 4)
ax.axis("scaled")
ax.set_xlim([-0.5, 2.5]), ax.set_ylim([-1.5, 1.5])


def circle(t):
    if t < 0:
        return 0, t
    if t > 1:
        return t, 1
    rad = pi / 2 * t
    return 1 - cos(rad), sin(rad)


def sin_acc(t):
    if t < 0:
        return 0, t
    if t > 1:
        return t, 1
    return (
        2 * (1 / 2 * t - sin(pi * t) / (2 * pi)),
        2 * (1 / 2 * t + sin(pi * t) / (2 * pi)),
    )


arr_t = np.arange(-0.5, 1.5, 0.01)
arr_x = np.empty_like(arr_t)
arr_y = np.empty_like(arr_t)

for i, t in enumerate(arr_t):
    arr_x[i], arr_y[i] = circle(t)
ax.plot(arr_x, arr_y)

for i, t in enumerate(arr_t):
    arr_x[i], arr_y[i] = sin_acc(t)
    arr_x[i] += 0.5
    arr_y[i] -= 0.5
ax.plot(arr_x, arr_y)

ax.quiver(-0.2, 0.1, 0.3, 0, color="red")

fig.savefig("1.png")


# %%
fig, ax = plt.subplots(1, 1, layout="constrained")
fig.suptitle("无法用 $y=f(x)$ 表达的曲线")
fig.set_size_inches(4, 4)
ax.axis("scaled")
ax.set_xlim([-2.5, 0.5]), ax.set_ylim([-1.5, 1.5])

arr_t = np.arange(0.5 * pi, 1.5 * pi, 0.01)
arr_x = np.empty_like(arr_t)
arr_y = np.empty_like(arr_t)

for i, t in enumerate(arr_t):
    arr_x[i], arr_y[i] = cos(t) * 2, sin(t)
ax.plot(arr_x, arr_y)
ax.axvline(-1, color="red")

ax.text(-0.9, 0, "$f(x)=?$")

fig.savefig("2.png")


# %%
fig, (ax_l, ax_r) = plt.subplots(1, 2, layout="constrained")
fig.suptitle("不可能发生的两种运动")
fig.set_size_inches(8, 4)

ax_l.set_title("位置传送")
ax_l.axis("scaled")
ax_l.set_xlim([-0.5, 2.5]), ax_l.set_ylim([-0.5, 2.5])

ax_r.set_title("瞬间变速")
ax_r.axis("scaled")
ax_r.set_xlim([-0.5, 2.5]), ax_r.set_ylim([-0.5, 2.5])

dt = 0.05


def animate():
    for t in np.arange(0, 2, dt):
        lx = 0 if t < 1 else t
        ly = t if t < 1 else 2
        ax_l.scatter(lx, ly, 3, color="blue")

        rx = 0 if t < 1 else t - 1
        ry = t
        ax_r.scatter(rx, ry, 3, color="blue")

        yield


ani = FuncAnimation(
    fig, lambda x: None, animate, interval=1000 * dt, repeat=True
)
ani.save("3.gif")


# %%
fig, axd = plt.subplot_mosaic(
    [
        ["p", "p", "x", "v_x", "a_x"],
        ["p", "p", "y", "v_y", "a_y"],
    ],
    layout="constrained",
)

fig.suptitle("圆弧+直线轨迹的运动过程")
fig.set_size_inches(13, 5)

ax_p = axd["p"]
ax_p.set_title(r"$\left<x,\ y\right>$")
ax_p.axis("scaled")
ax_p.set_xlim([-1, 1.5]), ax_p.set_ylim([-1, 1.5])

ax_x, ax_y = axd["x"], axd["y"]
ax_vx, ax_vy = axd["v_x"], axd["v_y"]
ax_ax, ax_ay = axd["a_x"], axd["a_y"]

for axn in ["x", "y", "v_x", "v_y", "a_x", "a_y"]:
    ax = axd[axn]
    ax.set_title(rf"${axn}$")
    ax.set_xlim([-0.5, 1.5]), ax.set_ylim([-1.5, 1.5])
    # ax.axis("scaled")

dt = 0.05


def animate():
    for t in np.arange(-0.5, 0, dt):
        x = -0.5
        y = t
        ax_p.scatter(x, y, 5, color="blue")
        ax_x.scatter(t, x, 3, color="blue")
        ax_y.scatter(t, y, 3, color="blue")

        vx = 0
        vy = 1
        ax_vx.scatter(t, vx, 3, color="blue")
        ax_vy.scatter(t, vy, 3, color="blue")

        ax = 0
        ay = 0
        ax_ax.scatter(t, ax, 3, color="blue")
        ax_ay.scatter(t, ay, 3, color="blue")

        yield

    for t in np.arange(0, 1, dt):
        ang = t * pi / 2

        x = 0.5 - cos(ang)
        y = sin(ang)
        ax_p.scatter(x, y, 5, color="red")
        ax_x.scatter(t, x, 3, color="red")
        ax_y.scatter(t, y, 3, color="red")

        vx = sin(ang)
        vy = cos(ang)
        ax_vx.scatter(t, vx, 3, color="red")
        ax_vy.scatter(t, vy, 3, color="red")

        ax = cos(ang)
        ay = -sin(ang)
        ax_ax.scatter(t, ax, 3, color="red")
        ax_ay.scatter(t, ay, 3, color="red")

        yield

    for t in np.arange(1, 1.5, dt):
        x = t - 0.5
        y = 1
        ax_p.scatter(x, y, 5, color="blue")
        ax_x.scatter(t, x, 3, color="blue")
        ax_y.scatter(t, y, 3, color="blue")

        vx = 1
        vy = 0
        ax_vx.scatter(t, vx, 3, color="blue")
        ax_vy.scatter(t, vy, 3, color="blue")

        ax = 0
        ay = 0
        ax_ax.scatter(t, ax, 3, color="blue")
        ax_ay.scatter(t, ay, 3, color="blue")

        yield


ani = FuncAnimation(
    fig, lambda x: print(".", end=""), animate, interval=1000 * dt, repeat=True
)
ani.save("4.gif")


# %%
fig, axd = plt.subplot_mosaic(
    [
        ["p", "p", "x", "v_x", "a_x"],
        ["p", "p", "y", "v_y", "a_y"],
    ],
    layout="constrained",
)

fig.suptitle("加速度采用线性连续函数")
fig.set_size_inches(13, 5)

ax_p = axd["p"]
ax_p.set_title(r"$\left<x,\ y\right>$")
ax_p.axis("scaled")
ax_p.set_xlim([-1, 1.5]), ax_p.set_ylim([-1, 1.5])

ax_x, ax_y = axd["x"], axd["y"]
ax_vx, ax_vy = axd["v_x"], axd["v_y"]
ax_ax, ax_ay = axd["a_x"], axd["a_y"]

for axn in ["x", "y", "v_x", "v_y", "a_x", "a_y"]:
    ax = axd[axn]
    ax.set_title(rf"${axn}$")
    ax.set_xlim([-0.5, 1.5]), ax.set_ylim([-1.5, 1.5])
    # ax.axis("scaled")

dt = 0.05


def animate():
    for t in np.arange(-0.5, 0, dt):
        x = -0.5
        y = t
        ax_p.scatter(x, y, 5, color="blue")
        ax_x.scatter(t, x, 3, color="blue")
        ax_y.scatter(t, y, 3, color="blue")

        vx = 0
        vy = 1
        ax_vx.scatter(t, vx, 3, color="blue")
        ax_vy.scatter(t, vy, 3, color="blue")

        ax = 0
        ay = 0
        ax_ax.scatter(t, ax, 3, color="blue")
        ax_ay.scatter(t, ay, 3, color="blue")

        yield

    for t in np.arange(0, 1, dt):
        ang = t * pi / 2

        x = 0.5 - cos(ang)
        y = sin(ang)
        ax_p.scatter(x, y, 5, color="red")
        ax_x.scatter(t, x, 3, color="red")
        ax_y.scatter(t, y, 3, color="red")

        vx = t**2 if t < 0.5 else 2 * t - 0.5 * (t - 0.5) ** 2
        vy = 1 - vx
        ax_vx.scatter(t, vx, 3, color="red")
        ax_vy.scatter(t, vy, 3, color="red")

        ax = 2 * t if t < 0.5 else 2 - (t - 0.5)
        ay = -ax
        ax_ax.scatter(t, ax, 3, color="red")
        ax_ay.scatter(t, ay, 3, color="red")

        yield

    for t in np.arange(1, 1.5, dt):
        x = t - 0.5
        y = 1
        ax_p.scatter(x, y, 5, color="blue")
        ax_x.scatter(t, x, 3, color="blue")
        ax_y.scatter(t, y, 3, color="blue")

        vx = 1
        vy = 0
        ax_vx.scatter(t, vx, 3, color="blue")
        ax_vy.scatter(t, vy, 3, color="blue")

        ax = 0
        ay = 0
        ax_ax.scatter(t, ax, 3, color="blue")
        ax_ay.scatter(t, ay, 3, color="blue")

        yield


ani = FuncAnimation(
    fig, lambda x: print(".", end=""), animate, interval=1000 * dt, repeat=True
)
ani.save("5.gif")


# %%
def poly_fx_d2(k: int):
    N = 2 * k + 3  # 2k+2 阶多项式共 2k+3 个待确定系数
    A = np.ndarray((N, N), dtype=np.float64)

    # 积分为 1
    for i in range(N):
        A[0, i] = 1 / (i + 1)

    # P(m)(0) = 0
    for m in range(0, k + 1):
        row = m + 1
        A[row, :m] = 0
        for i in range(m, N):
            A[row, i] = factorial(i) / factorial(i - m) * 0 ** (i - m)

    # P(m)(1) = 0
    for m in range(0, k + 1):
        row = m + 1 + k + 1
        A[row, :m] = 0
        for i in range(m, N):
            A[row, i] = factorial(i) / factorial(i - m) * 1 ** (i - m)

    b = np.zeros(N)
    b[0] = 1

    # print(A, b)
    d2_ai = np.linalg.solve(A, b)
    # fx_d2 = lambda t: d2_ai @ t ** np.arange(len(ai))

    d1_ai = np.ndarray([len(d2_ai) + 1], dtype=np.float64)
    d1_ai[0] = 0
    d1_ai[1:] = d2_ai / np.arange(1, len(d2_ai) + 1, dtype=np.float64)

    ai = np.ndarray([len(d1_ai) + 1], dtype=np.float64)
    ai[0] = 0
    ai[1:] = d1_ai / np.arange(1, len(d1_ai) + 1, dtype=np.float64)

    return lambda t: ai @ t ** np.arange(len(ai))


def plot(ax, k, dx, dy):
    _fx = poly_fx_d2(k)

    def f(t):
        if t < 0:
            x, y = 0, t
        elif t > 1:
            x, y = t, 1
        else:
            x, y = _fx(t), 1 - _fx(1 - t)
        return x + dx, y + dy

    arr_t = np.arange(-0.5, 1.5, 0.01)
    arr_x = np.empty_like(arr_t)
    arr_y = np.empty_like(arr_t)

    for i, t in enumerate(arr_t):
        arr_x[i], arr_y[i] = f(t)
    ax.plot(arr_x, arr_y)


fig, ax = plt.subplots(1, 1, layout="constrained")
fig.set_size_inches(8, 8)
ax.axis("scaled")
ax.set_xlim([0, 3]), ax.set_ylim([-2, 1])

N = 11
dx = dy = 0.0
for k in range(N + 1):
    dx += 0.2
    dy -= 0.2
    plot(ax, k, dx, dy)
    ax.text(dx, dy + 1, k)

fig.suptitle(f"$f_x''$ 0~{N} 阶连续的对比")
fig.savefig("6.png")