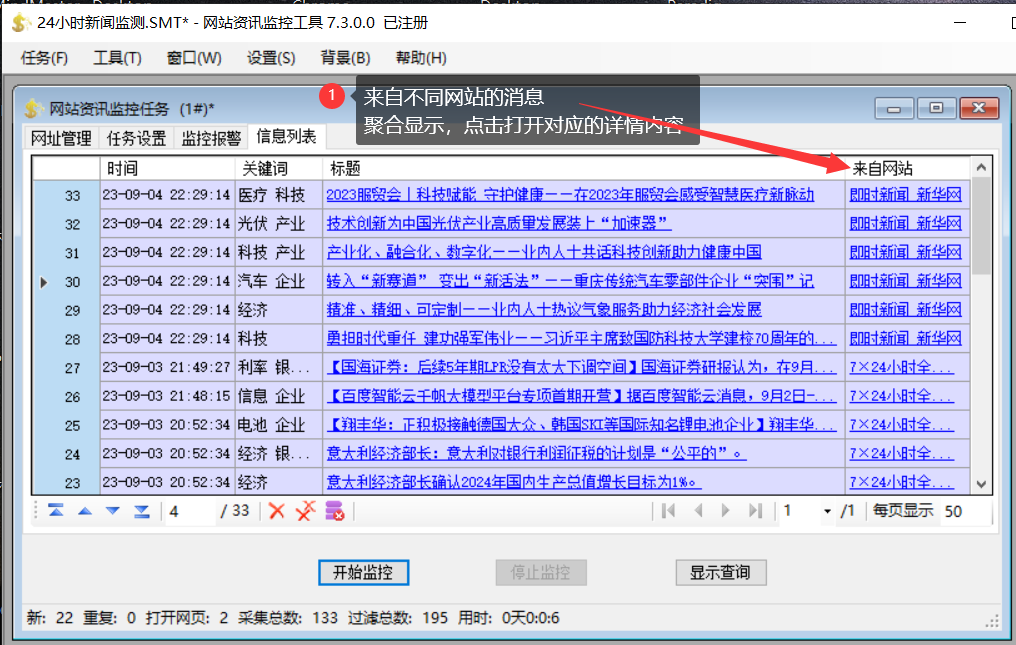
对于一组数据,并查集主要支持两个动作:
-
union(p,q) - 将 p 和 q 两个元素连接起来。
-
find(p) - 查询 p 元素在哪个集合中。
-
isConnected(p,q) - 查看 p 和 q 两个元素是否相连接在一起。
在上一小节中,我们用 id 数组的形式表示并查集,实际操作过程中查找的时间复杂度为 O(1),但连接效率并不高。
本小节,我们将用另外一种方式实现并查集。把每一个元素,看做是一个节点并且指向自己的父节点,根节点指向自己。如下图所示,节点 3 指向节点 2,代表 3 和 2 是连接在一起的,节点2本身是根节点,所以指向自己。

同样用数组表示并查集,但是下面一组元素用 parent 表示当前元素指向的父节点,每个元素指向自己,都是独立的。


如果此时操作 union(4,3),将元素 4 指向元素 3:

数组也进行相应改变:

判断两个元素是否连接,只需要判断根节点是否相同即可。
如下图,节点 4 和节点 9 的根节点都是 8,所以它们是相连的。

连接两个元素,只需要找到它们对应的根节点,使根节点相连,那它们就是相连的节点。
假设要使上图中的 6 和 4 相连,只需要把 6 的根节点 5 指向 4 的根节点 8 即可。
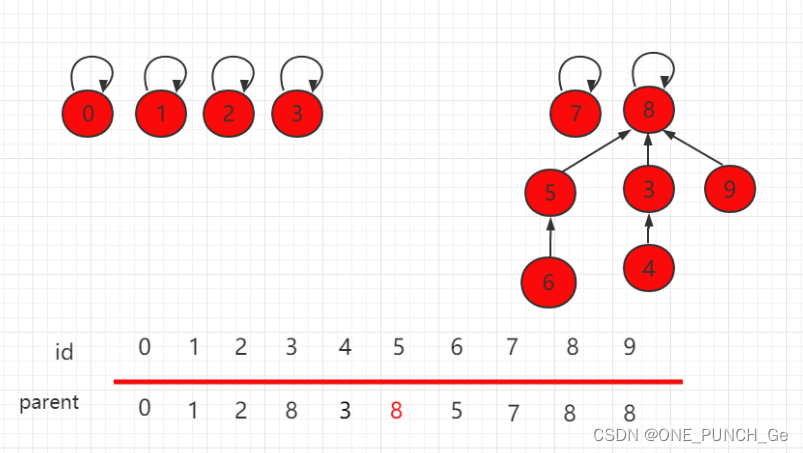
构建这种指向父节点的树形结构, 使用一个数组构建一棵指向父节点的树,parent[i] 表示 i 元素所指向的父节点。
...
private int[] parent;
private int count; // 数据个数
...查找过程, 查找元素 p 所对应的集合编号,不断去查询自己的父亲节点, 直到到达根节点,根节点的特点 parent[p] == p,O(h) 复杂度, h 为树的高度。
...
private int find(int p){
assert( p >= 0 && p < count );
while( p != parent[p] )
p = parent[p];
return p;
}
...合并元素 p 和元素 q 所属的集合,分别查询两个元素的根节点,使其中一个根节点指向另外一个根节点,两个集合就合并了。这个操作是 O(h) 的时间复杂度,h 为树的高度。
public void unionElements(int p, int q){
int pRoot = find(p);
int qRoot = find(q);
if( pRoot == qRoot )
return;
parent[pRoot] = qRoot;
}Java 实例代码
UnionFind2.java 文件代码:
package runoob.union;
/**
* 第二版unionFind
*/
public class UnionFind2 {
// 我们的第二版Union-Find, 使用一个数组构建一棵指向父节点的树
// parent[i]表示第一个元素所指向的父节点
private int[] parent;
private int count; // 数据个数
// 构造函数
public UnionFind2(int count){
parent = new int[count];
this.count = count;
// 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
for( int i = 0 ; i < count ; i ++ )
parent[i] = i;
}
// 查找过程, 查找元素p所对应的集合编号
// O(h)复杂度, h为树的高度
private int find(int p){
assert( p >= 0 && p < count );
// 不断去查询自己的父亲节点, 直到到达根节点
// 根节点的特点: parent[p] == p
while( p != parent[p] )
p = parent[p];
return p;
}
// 查看元素p和元素q是否所属一个集合
// O(h)复杂度, h为树的高度
public boolean isConnected( int p , int q ){
return find(p) == find(q);
}
// 合并元素p和元素q所属的集合
// O(h)复杂度, h为树的高度
public void unionElements(int p, int q){
int pRoot = find(p);
int qRoot = find(q);
if( pRoot == qRoot )
return;
parent[pRoot] = qRoot;
}
}