定义

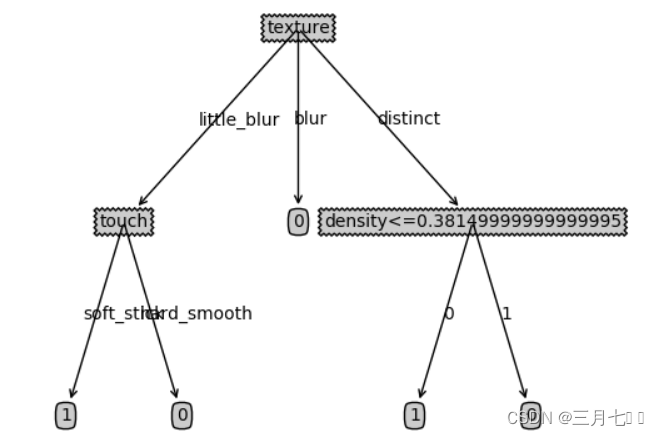
this 是 C++ 中的一个关键字，也是一个 const 指针，它指向当前对象，通过它可以访问当前对象的所有成员。

this的介绍

下面来看一下关于this这个关键字的实例！

class Data
{
private:
    int _year;
    int _month;
    int _day;
public:
    void Init(int year,int month,int day)
    {

        cout << "this的地址"<<this << endl;
        _year = year;
        _month = month;
        _day = day;
    }
}
int main()
{
    Data D1;
    Data D2;
    cout <<"D1的地址："<< & D1 << endl;
    cout <<"D2的地址："<< & D2 << endl;
    D1.Init(2013,11,15);
    D2.Init(2013, 11, 16);
}

通过观察上述代码，在main函数内部里，当使用Init函数时，并没有对Init函数进行传相应类的参数，那么编译器是如何将其正确赋值给相应的类呢？

这时就引出了C++的关键字this！编译器通过this关键字来自动匹配传递的参数！下面来看一下msdn中关于对this关键字的简单介绍！

简单介绍一下上述的意思，“this”指针仅仅存在于class,struct,union类型，它指向成员功能调用的目标，静态变量没有this这个指针！

this指针内部详细介绍！

通过下面代码，可以对this指针会有更深一步的认识！

class Data
{
private:
    int _year;
    int _month;
    int _day;
public:
    void Init(int year,int month,int day)
    {

        //this在实参和形参的位置不能显写，但是在类中变量可以显写！
        //this = nullptr;
        //通过在类中对this的操作，可以证明this指针确实存在！
        cout << "this的地址"<<this << endl;
       /* this->*/_year = year;
        /*this->*/_month = month;
        _day = day;
    }
    void print()
    {
        cout << _year << "-";
        cout << _month << "-";
        cout << _day;
        cout << endl;
    }
};

int main()
{
    Data D1;
    Data D2;

    //通过观察D1，D2的地址，可以看出D1中的this的地址和D1的地址相同，可以推出this指针实际上是指向类的地址的指针的！
    cout <<"D1的地址："<< & D1 << endl;
    cout <<"D2的地址："<< & D2 << endl;
    D1.Init(2013,11,15);
    D2.Init(2013, 11, 16);
    D1.print();
    D2.print();
}

上述代码运行调试过后结果入下：

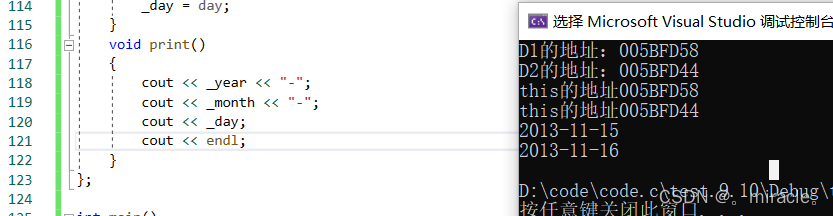
通过上述调试的结果，可以更深了解this指针！

this指针的特性

1. this指针的类型：类类型* const，即成员函数中，不能给this指针赋值。

上实例当对this指针赋予nullptr时，编译器会报错，错误信息入下：

2. 只能在“成员函数”的内部使用。

3. this指针本质上是“成员函数”的形参，当对象调用成员函数时，将对象地址作为实参传递给

this形参。所以对象中不存储this指针。（可以通过对类的大小来判断类中是否存在了this指针！）

4. this指针是“成员函数”第一个隐含的指针形参，一般情况由编译器通过ecx寄存器自动传

递，不需要用户传递。

this到底是什么

this 实际上是成员函数的一个形参，在调用成员函数时将对象的地址作为实参传递给 this。不过 this 这个形参是隐式的，它并不出现在代码中，而是在编译阶段由编译器默默地将它添加到参数列表中。
this 作为隐式形参，本质上是成员函数的局部变量，所以只能用在成员函数的内部，并且只有在通过对象调用成员函数时才给 this 赋值。

至此，关于this指针的介绍结束，若还有其他特性，欢迎读者来进行补充，也欢迎各位指出不足！