Day60｜单调栈part03：84.柱状图中最大的矩形

news2025/1/20 13:31:26

柱状图中最大的矩形

leetcode链接：力扣题目链接

视频链接：单调栈，又一次经典来袭！ LeetCode：84.柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

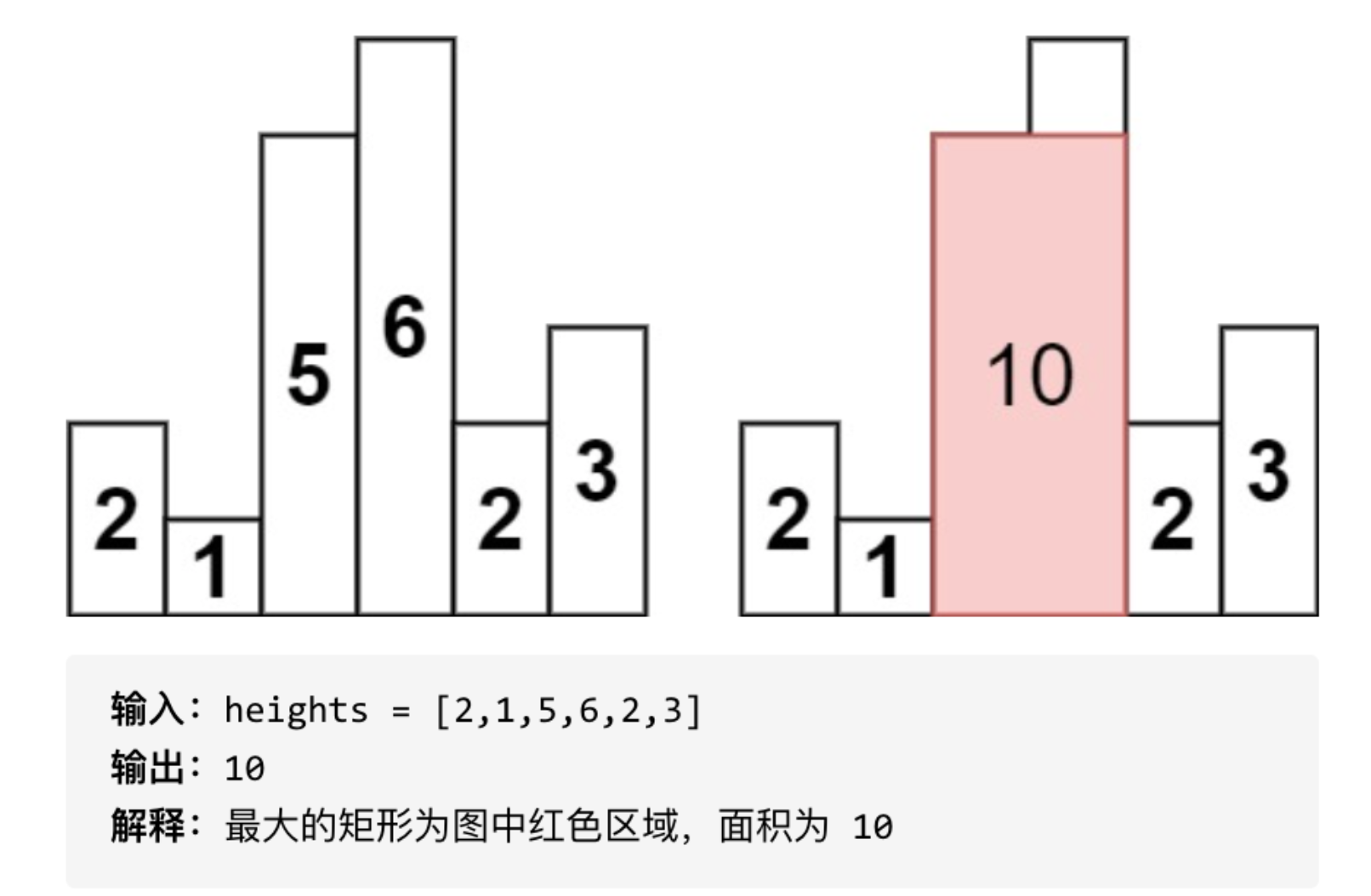
这是一道hard题，首先是暴力解法，任意遍历两个数，然后求最值：

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int sum = 0;
        for (int i = 0; i < heights.size(); i++) {
            int left = i;
            int right = i;
            for (; left >= 0; left--) {
                if (heights[left] < heights[i]) break;
            }
            for (; right < heights.size(); right++) {
                if (heights[right] < heights[i]) break;
            }
            int w = right - left - 1;
            int h = heights[i];
            sum = max(sum, w * h);
        }
        return sum;
    }
};

如上代码并不能通过leetcode，超时了，因为时间复杂度是O(n^2)。

双指针法

没想出来，直接看题解

难就难在本题要记录记录每个柱子左边第一个小于该柱子的下标，而不是左边第一个小于该柱子的高度。

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        vector<int> minLeftIndex(heights.size());
        vector<int> minRightIndex(heights.size());
        int size = heights.size();

        // 记录每个柱子 左边第一个小于该柱子的下标
        minLeftIndex[0] = -1; // 注意这里初始化，防止下面while死循环
        for (int i = 1; i < size; i++) {
            int t = i - 1;
            // 这里不是用if，而是不断向左寻找的过程
            while (t >= 0 && heights[t] >= heights[i]) t = minLeftIndex[t];
            minLeftIndex[i] = t;
        }
        // 记录每个柱子 右边第一个小于该柱子的下标
        minRightIndex[size - 1] = size; // 注意这里初始化，防止下面while死循环
        for (int i = size - 2; i >= 0; i--) {
            int t = i + 1;
            // 这里不是用if，而是不断向右寻找的过程
            while (t < size && heights[t] >= heights[i]) t = minRightIndex[t];
            minRightIndex[i] = t;
        }
        // 求和
        int result = 0;
        for (int i = 0; i < size; i++) {
            int sum = heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1);
            result = max(sum, result);
        }
        return result;
    }
};

单调栈解法

那么因为本题是要找每个柱子左右两边第一个小于该柱子的柱子，所以从栈头（元素从栈头弹出）到栈底的顺序应该是从大到小的顺序！

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int result = 0;
        stack<int> st;
        heights.insert(heights.begin(), 0); // 数组头部加入元素0
        heights.push_back(0); // 数组尾部加入元素0
        st.push(0);

        // 第一个元素已经入栈，从下标1开始
        for (int i = 1; i < heights.size(); i++) {
            if (heights[i] > heights[st.top()]) { // 情况一
                st.push(i);
            } else if (heights[i] == heights[st.top()]) { // 情况二
                st.pop(); // 这个可以加，可以不加，效果一样，思路不同
                st.push(i);
            } else { // 情况三
                while (!st.empty() && heights[i] < heights[st.top()]) { // 注意是while
                    int mid = st.top();
                    st.pop();
                    if (!st.empty()) {
                        int left = st.top();
                        int right = i;
                        int w = right - left - 1;
                        int h = heights[mid];
                        result = max(result, w * h);
                    }
                }
                st.push(i);
            }
        }
        return result;
    }
};