🌈🌈🌈机器学习 实战系列 总目录
本篇文章的代码运行界面均在Pycharm中进行
本篇文章配套的代码资源已经上传
SVM分类实战1之简单SVM分类
SVM分类实战2线性SVM
SVM分类实战3非线性SVM
3、不同软间隔C值
3.1 数据标准化的影响
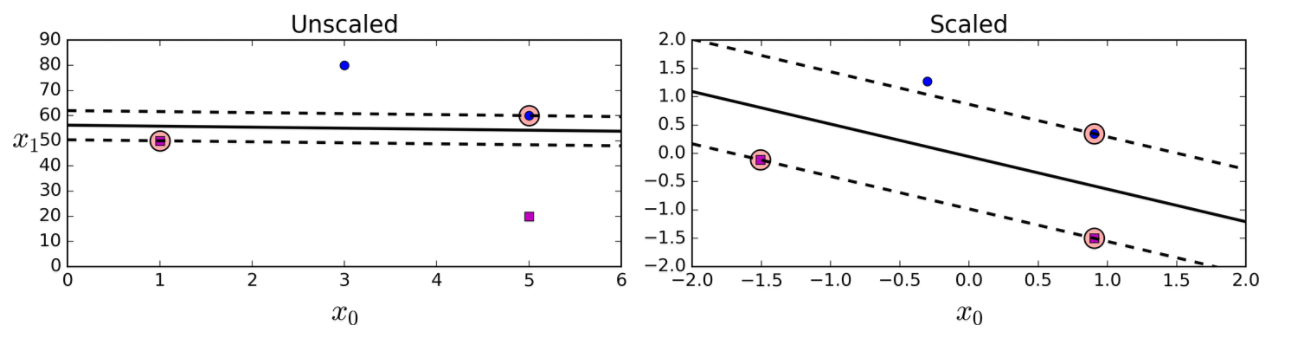
如图左边是没有使用标准化操作的分类结果,右边使用了标准化操作,很显然右边分类的精度更高,能够更好的将数据进行分类
3.2 软间隔
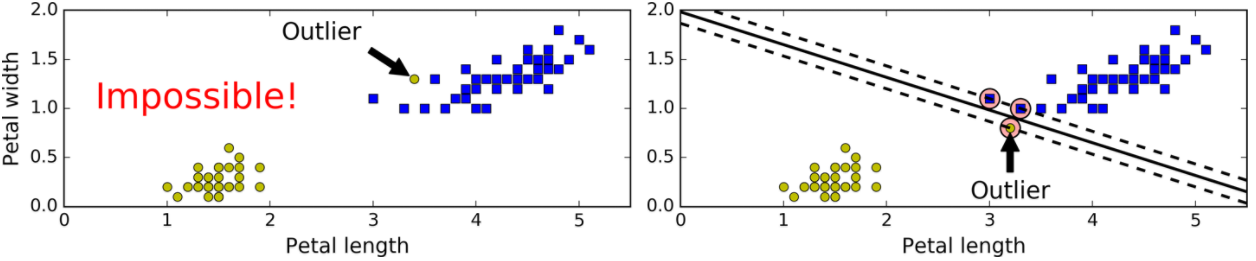
如左图所示,存在一个离群点,如果严格按照SVM一定要全部分类正确去做,不可能找到一个回归线将两类数据分开。右边的图,它的决策边界要求放松了一点,但是可以基本拟合数据的分类情况。这个就是软间隔需要做的事情,它可以控制当前的决策边界别那么严格了,错一点也没关系,使用超参数C控制软间隔程度。
import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
iris=datasets.load_iris()
X = iris["data"][:,(2,3)] # petal length, petal width
y = (iris["target"] == 2).astype(np.float64) # Iris-Viginica
svm_clf = Pipeline((
('std',StandardScaler()),
('linear_svc',LinearSVC(C=1))
))
svm_clf.fit(X,y)
svm_clf.predict([[5.5,1.7]])
- 导包
- 取出鸢尾花数据
- 取出两列作为输入数据
- 取出标签数据
svm_clf分类器- 标准化操作
- 线性支持向量机,C值指定为1
- 训练处一个基本模型
- 随便传进去两个值,预测出结果属于第二个类别
打印结果:
array([1.])
3.3 不同C值对比
scaler = StandardScaler()
svm_clf1 = LinearSVC(C=1,random_state = 42)
svm_clf2 = LinearSVC(C=100,random_state = 42)
scaled_svm_clf1 = Pipeline((
('std',scaler),
('linear_svc',svm_clf1)
))
scaled_svm_clf2 = Pipeline((
('std',scaler),
('linear_svc',svm_clf2)
))
scaled_svm_clf1.fit(X,y)
scaled_svm_clf2.fit(X,y)
这段代码展示了如何使用scikit-learn库中的Pipeline和StandardScaler来构建和训练两个不同的线性支持向量机分类器,其中一个使用较小的正则化参数C,另一个使用较大的正则化参数C。下面是对代码的解释:
-
scaler = StandardScaler(): 这行代码创建了一个名为scaler的标准化器对象。StandardScaler用于将数据标准化,即将特征缩放到均值为0,方差为1的标准正态分布。 -
svm_clf1 = LinearSVC(C=1, random_state=42): 这行代码创建了一个线性支持向量机分类器svm_clf1,并设置正则化参数C为1。random_state参数用于设置随机数生成器的种子,以确保结果的可重现性。 -
svm_clf2 = LinearSVC(C=100, random_state=42): 这行代码创建了另一个线性支持向量机分类器svm_clf2,并设置较大的正则化参数C为100,同时也设置了相同的随机种子。 -
scaled_svm_clf1和scaled_svm_clf2是使用Pipeline构建的两个分类器,它们包含了标准化和线性支持向量机两个步骤。具体来说,scaled_svm_clf1将数据首先标准化,然后应用svm_clf1进行分类,而scaled_svm_clf2将数据首先标准化,然后应用svm_clf2进行分类。 -
Pipeline对象由一个元组构成,元组中包含了一系列的步骤,每个步骤都由一个名称和一个估算器(estimator)组成。在这里,第一个步骤使用了标准化器std,第二个步骤使用了线性支持向量机分类器linear_svc。 -
scaled_svm_clf1.fit(X, y)和scaled_svm_clf2.fit(X, y)分别用于训练两个分类器,其中X是输入特征,y是目标标签。这将使模型学习如何根据输入数据对鸢尾花进行分类。
通过这种方式,可以比较两个不同正则化参数C的线性SVM分类器的性能,并选择适合你数据的模型。通常,较大的C值表示模型对分类错误的惩罚更大,可能会导致更复杂的模型,而较小的C值则表示模型对分类错误的惩罚较小,可能导致更简单的模型。选择适当的C值取决于具体的问题和数据。
3.4 展示训练结果
b1 = svm_clf1.decision_function([-scaler.mean_ / scaler.scale_])
b2 = svm_clf2.decision_function([-scaler.mean_ / scaler.scale_])
w1 = svm_clf1.coef_[0] / scaler.scale_
w2 = svm_clf2.coef_[0] / scaler.scale_
svm_clf1.intercept_ = np.array([b1])
svm_clf2.intercept_ = np.array([b2])
svm_clf1.coef_ = np.array([w1])
svm_clf2.coef_ = np.array([w2])
plt.figure(figsize=(14,4.2))
plt.subplot(121)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^", label="Iris-Virginica")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs", label="Iris-Versicolor")
plot_svc_decision_boundary(svm_clf1, 4, 6,sv=False)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="upper left", fontsize=14)
plt.title("$C = {}$".format(svm_clf1.C), fontsize=16)
plt.axis([4, 6, 0.8, 2.8])
plt.subplot(122)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
plot_svc_decision_boundary(svm_clf2, 4, 6,sv=False)
plt.xlabel("Petal length", fontsize=14)
plt.title("$C = {}$".format(svm_clf2.C), fontsize=16)
plt.axis([4, 6, 0.8, 2.8])
打印结果:
[0.86509158 2.24724474]
[1.74772456 3.14504837]
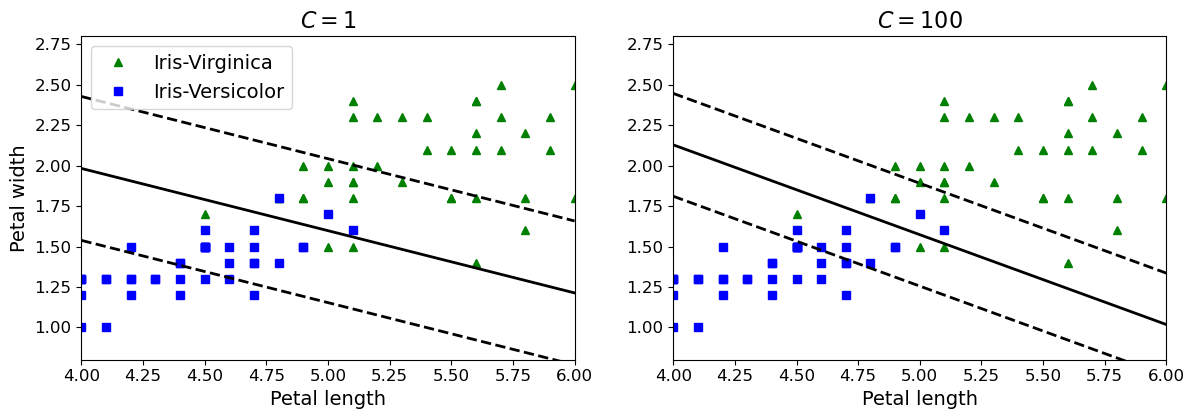
如左图,当C值设置的比较小的时候,得到的决策边界比较大,但是会出现一些错误,设置比较的大的时候就会比较严格,就容易出现过拟合的风险
- 在右侧,使用较高的C值,分类器会减少误分类,但最终会有较小间隔。
- 在左侧,使用较低的C值,间隔要大得多,但很多实例最终会出现在间隔之内。
SVM分类实战1之简单SVM分类
SVM分类实战2线性SVM
SVM分类实战3非线性SVM