---

前言

1、翻转二叉树
2、对称二叉树
3、完全二叉树的结点个数

---

一、翻转二叉树（力扣226）

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

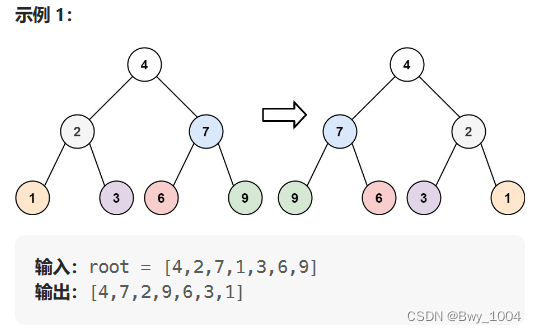
1、递归法

1、使用前序遍历

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root==null)return root;
        TreeNode temp = root.left;
        root.left=root.right;
        root.right=temp;
        invertTree(root.left);
        invertTree(root.right);
        return root;
    }
}

2、使用后序遍历

class Solution {
    public TreeNode invertTree(TreeNode root) {        
        if(root==null)return root;
        invertTree(root.left);
        invertTree(root.right);
        TreeNode temp = root.left;
        root.left=root.right;
        root.right=temp;
        return root;
    }
}

2、迭代法

1、层序遍历

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {return null;}
        ArrayDeque<TreeNode> deque = new ArrayDeque<>();
        deque.offer(root);
        while (!deque.isEmpty()) {
            int size = deque.size();
            while (size-- > 0) {
                TreeNode node = deque.poll();
                swap(node);
                if (node.left != null) {deque.offer(node.left);}
                if (node.right != null) {deque.offer(node.right);}
            }
        }
        return root;
    }
    public void swap(TreeNode root) {
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;
    }
}

二、对称二叉树（力扣101）

给定一个二叉树，检查它是否是镜像对称的。

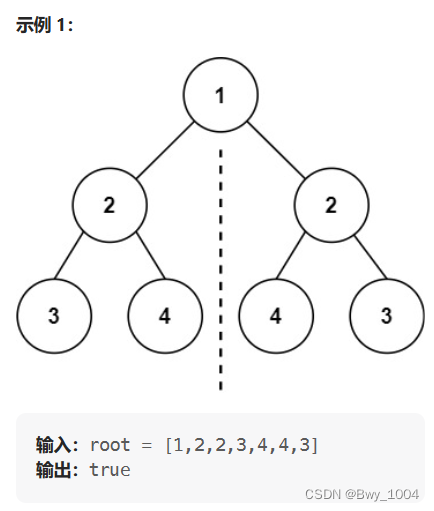
前中后序只能采用后序遍历
判断左子树右子树是否可以翻转，并将结果返回给根节点
左为空 右不为空 return false
右为空 左不为空 return false
左为空 右为空 return true
左 右数值不相等 return false
左 右数值相等 进行递归判断下一层结点

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if(root!=null){
            return true;
        }
        return Compare(root.left,root.right);
    }
    public boolean Compare(TreeNode left,TreeNode right){
        //避免后续出现空指针的情况 所以先处理为空的条件
        if(left==null && right!=null) return false;
        else if(left!=null && right==null) return false;
        else if(left==null && right==null) return true;
        else if(left.val!=right.val) return false;

        //左右“节点”都不为空 且数值相等的情况
        //此时才进行递归 进行下一层判断
        boolean outside = Compare(left.left,right.right);
        boolean inside = Compare(left.right,right.left);

        boolean isSame = outside && inside;
        return isSame; 
    }
}

三、完全二叉树的结点个数（力扣222）

给出一个完全二叉树，求出该树的节点个数。

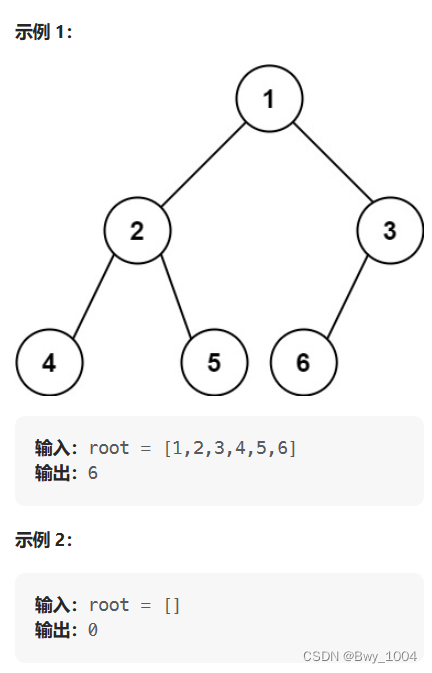
把完全二叉树当做一棵普通的二叉树
可以用前中后层序遍历去统计结点数目

class Solution {
    public int countNodes(TreeNode root) {
        //后序遍历
        if(root==null)return 0;
        int leftNum = countNodes(root.left);
        int rightNum = countNodes(root.right);
        return leftNum+rightNum+1;

    }
}

利用完全二叉树特性

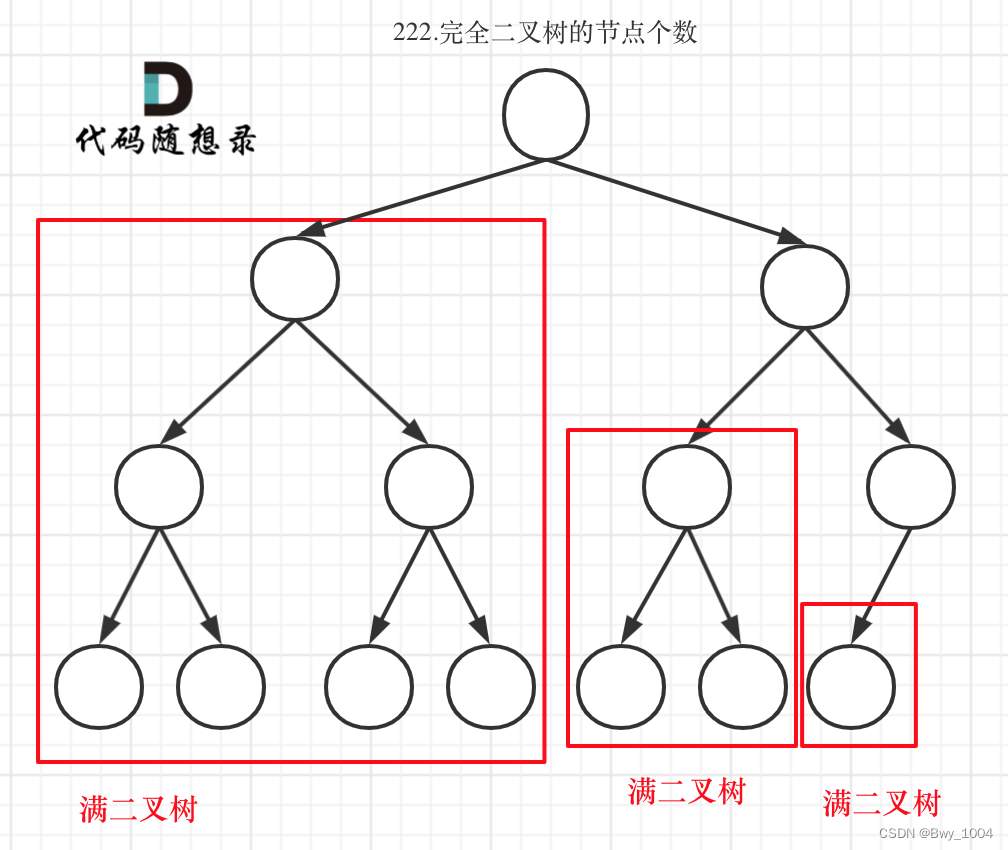
较难理解

class Solution {
    public int countNodes(TreeNode root) {
        //后序遍历
        // if(root==null)return 0;
        // int leftNum = countNodes(root.left);
        // int rightNum = countNodes(root.right);
        // return leftNum+rightNum+1;

        //完全二叉树特性
        if(root==null) return 0;
        TreeNode leftNode = root.left;
        TreeNode rightNode = root.right;
         int leftDepth = getDepth(root.left);
        int rightDepth = getDepth(root.right);
        if(leftDepth==rightDepth){//说明是满二叉树
            return (1 << leftDepth) + countNodes(root.right);
        }else {// 右子树是满二叉树
            return (1 << rightDepth) + countNodes(root.left);
        }
    }

        private int getDepth(TreeNode root) {
        int depth = 0;
        while (root != null) {
            root = root.left;
            depth++;
        }
        return depth;
    }
}

---