删去k个数字后的最小值
- 思路
- 贪心算法
- JAVA实现1
- JAVA实现2
给出一个整数,从该整数中去掉k个数字,要求剩下的数字形成的新整数尽可能小。应该如何选取被去掉的数字?
其中整数的长度大于或等于k,给出的整数的大小可以超过long类型的数字范
围。
思路
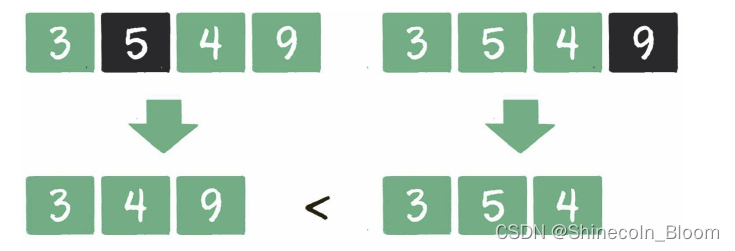
但我们不妨把问题简化一下:如果只删除1个数字,如何让新整数的值最小?
数字的大小固然重要,数字的位置则更加重要。
无论删除哪一个数字,最后的结果都是从9位整数变成8位整数。既然同
样是8位整数,显然应该优先把高位的数字降低,这样对新整数的值影响最大。
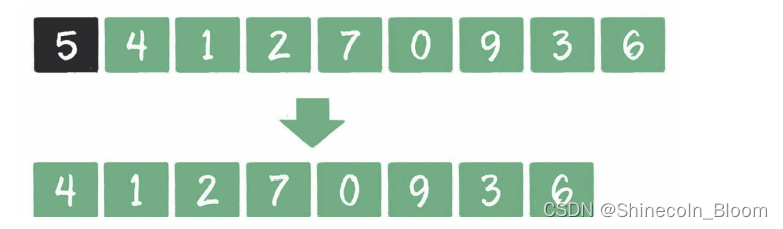
关键点:如何把高位数字减低
把原整数的所有数字从左到右进行比较,如果发现某一位数字大于它右面的数字,那么在删除该数字后,必然会使该数位的值降低,因为右面比它小的数字顶替了它的位置。
贪心算法
依次求得局部最优解,最终得到全局最优解的思想,叫作贪心算法。
在本题中:每一步都要求得到删除一个数字后的最小值,经历3次,相当于求出了删除k(k=3)个数字后的最小值。
第一步
第二步
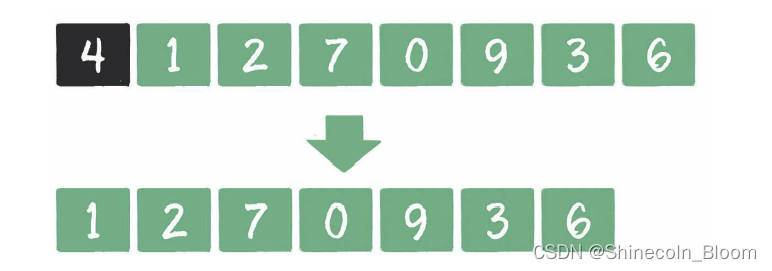
第三步
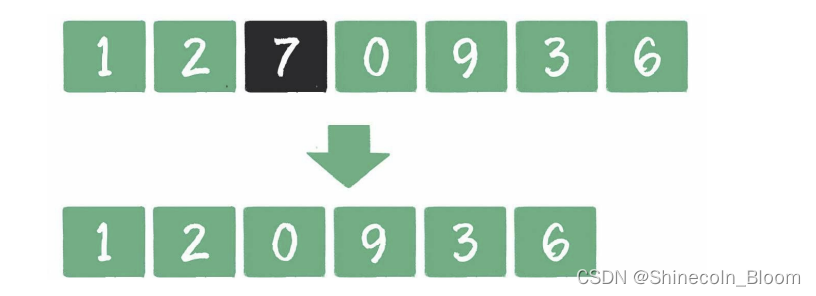
JAVA实现1
public class removeNDigits {
//清除字符串左边的数字0
private static String removeZero(String num){
for (int i=0;i<num.length()-1;i++){
if(num.charAt(0)!='0'){
//首元素不为零,跳出,不用删0了
break;
}
//删除第一个位置的0(之后继续循环)
num = num.substring(1,num.length());
}
return num;
}
/**
*
* @param num 原整数
* @param k 删除数量
* @return
*/
public static String removekDigits(String num,int k){
String numNew = num;
for (int i=0;i<k;i++){
//是否截取字符串的标记
boolean hasCut= false;
//从左向右遍历,找到比自己右侧数字大的数字并删除
//substring截取不包括右边的下标
for (int j=0;j<numNew.length()-1;j++){
if(numNew.charAt(j)>numNew.charAt(j+1)){
numNew = numNew.substring(0,j)+numNew.substring(j+1,numNew.length());
hasCut = true;
//完成一轮了(一共k)
break;
}
}
//在一轮中,如果没有找到要删除的数字,则删除最后一个数字
if (!hasCut){
numNew = numNew.substring(0,numNew.length()-1);
}
//清除整数左侧的数字0
numNew=removeZero(numNew);
}
//如果整数的所有数字都被删除了,直接返回0
if(numNew.length()==0){
return "0";
}
return numNew;
}
测试类
public static void main(String[] args) {
System.out.println(removekDigits("30200",1));
System.out.println(removekDigits("1593212",1));
System.out.println(removekDigits("1593212",2));
System.out.println(removekDigits("1593212",3));
}
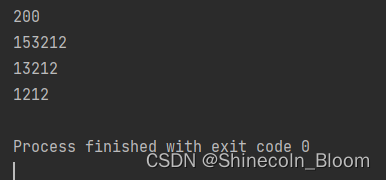
代码使用了两层循环,外层循环次数就是要删除的数字个数k,内层循环
从左到右遍历所有数字。当遍历到需要删除的数字时,利用字符串的自身方法subString()把对应的数字删除,并重新拼接字符串。
时间复杂度是O(kn)。
JAVA实现2
以遍历数字作为外循环,以k作为内循环
利用栈来实现
栈的特性,在遍历原整数的数字时,让所有数字一个一个入栈,当某个数字需要删除时,让该数字出栈。最后,程序把栈中的元素转化为字符串类型的结果。
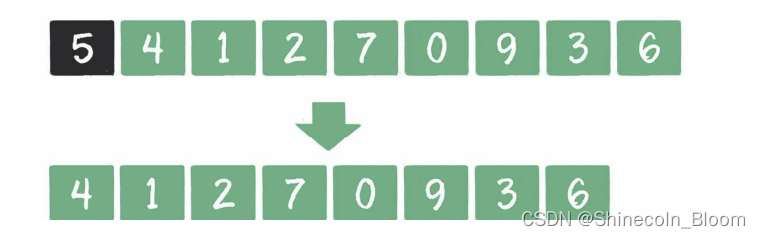
例子:541 270 936,k=3
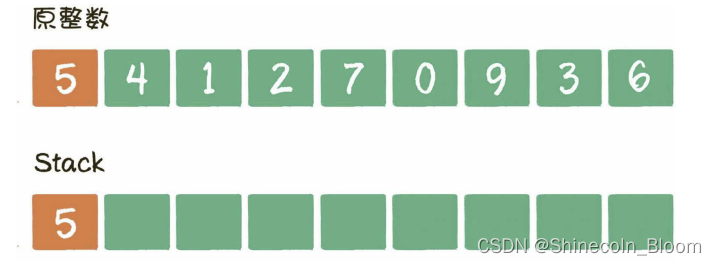
当遍历到数字4时,发现栈顶5>4,栈顶5出栈,数字4入栈。
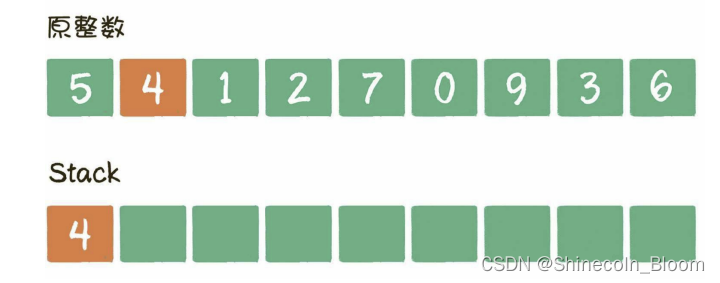
当遍历到数字1时,发现栈顶4>1,栈顶4出栈,数字1入栈
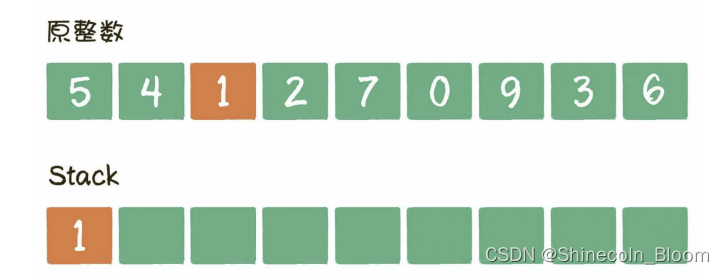
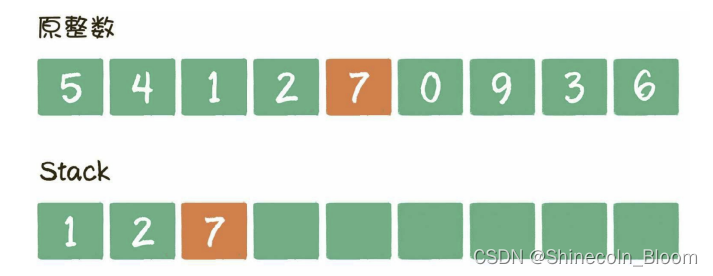
遍历数字0,发现栈顶7>0,栈顶7出栈,数字0入栈。
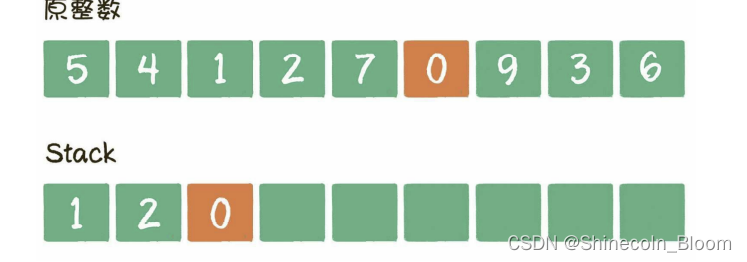
此时k的次数已经用完,无须再比较,让剩下的数字一起入栈即可
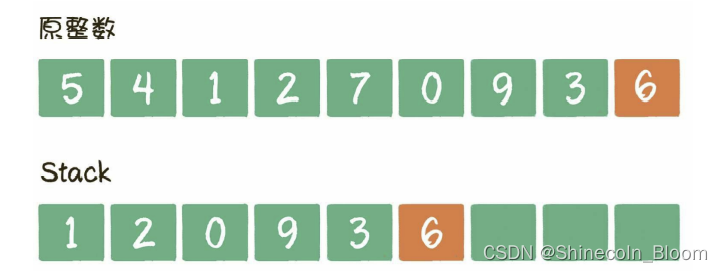
遍历的时间复杂度是O(n),把栈转化为字符串的时间复杂度也是O(n),所以最终的时间复杂度是O(n)。
程序中利用栈来回溯遍历过的数字及删除数字,所以程序的空间复杂度是O(n)。