中缀表达式就是我们平时运算表达式,其特点是运算符总是处于两个运算对象之间。但是该表达式计算机处理起来较为麻烦,会将其转写成后缀表达式,后缀表达式也叫逆波兰表达式,后缀表达式的特点是每个运算符都置于两个运算对象之后。此篇的部分内容参考博文地址为:C++栈的应用-中缀转后缀。
文章目录
- 1. 后缀表达式(由波兰科学家在20世纪50年代提出)
- 2. 中缀转后缀算法
- 2.1 中缀转后缀算法
- 2.2 对 `8 + (3 - 1) * 5`的转换过程进行实例分析。
- 3. 中缀转后缀算法的代码实现
- 3.1 提供栈的基本操作函数
- 3.2 一些判断函数
- 3.3 按转换规则的实现代码
- 3.4 运行结果
- 3.5 整体代码
1. 后缀表达式(由波兰科学家在20世纪50年代提出)
- 将运算符放在数字后面–>符合计算机运算
- 我们习惯的数学表达式叫做中缀表达式–>符合人类思考习惯
实例
- 5+4 -->5 4 +
- 1+2*3 ->1 2 3 * +
- 8 + (3 - 1) * 5 -> 8 3 1 - 5 * + (后面也是以此为案例)
2. 中缀转后缀算法
2.1 中缀转后缀算法
遍历中缀表达式中的数字和符号:
-
对于数字:直接输出
-
对于符号:
- 左括号:进栈
- 运算符号:与栈顶符号进行优先级比较
- 若栈顶符号优先级低:此符号进栈(默认栈顶若是左括号,左括号优先级最低)
- 若栈顶符号优先级不低:将栈顶符号弹出并输出,之后进栈
- 右括号:将栈顶符号弹出并输出,直到匹配左括号,括号扔掉
-
遍历结束:将栈中的所有符号弹出并输出
运算符优先级:

2.2 对 8 + (3 - 1) * 5的转换过程进行实例分析。
前面在C++数据结构X篇_08_C++实现栈的顺序存储与链式存储中讲到了栈中数据先进后出。
以下是遍历的过程:
(1)遍历到1位置
8数字直接输出,+运算符进栈,左括号进栈,-进栈

(2)遍历到右括号位置
输出-,匹配到左括号,将左括号和右括号扔掉

(3)遍历到*位置
由于*优先级高于+,进栈
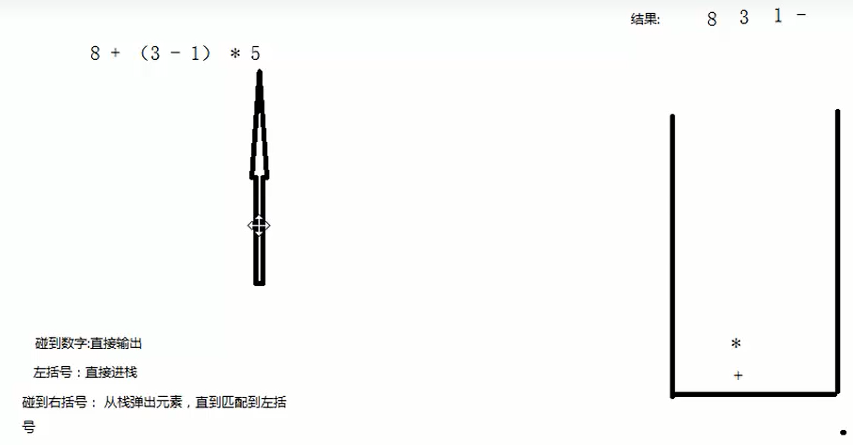
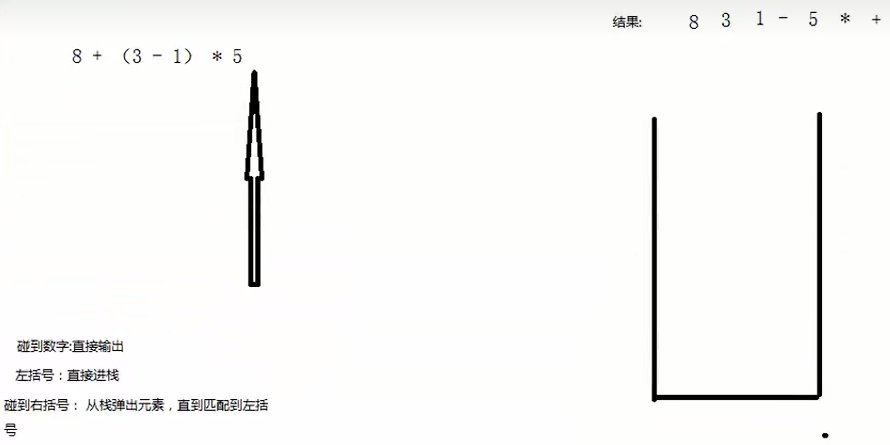
(4)遍历结束
将栈中的所有符号弹出并输出
3. 中缀转后缀算法的代码实现
下面将会用程序的方法输出该案例,这里栈选用链式存储的栈,具体介绍可见C++实现栈的顺序存储与链式存储。
3.1 提供栈的基本操作函数
//有关栈的基本操作
//节点
class linknode
{
public:
linknode* next;
};
//自定义数据
class my_data
{
public:
linknode* node;
char c;
};
//链式栈
class linkstack
{
public:
linknode head;
int size;
};
//初始化栈
linkstack* init_linkstack()
{
linkstack* stack=new linkstack;
stack->head.next=NULL;
stack->size=0;
return stack;
}
//入栈
void push_linkstack(linkstack* stack,linknode* data)
{
data->next=stack->head.next;
stack->head.next=data;
stack->size++;
}
//出栈
void pop_linkstack(linkstack* stack)
{
stack->head.next=stack->head.next->next;
stack->size--;
}
//返回栈顶元素
linknode* top_linkstack(linkstack* stack)
{
return stack->head.next;
}
3.2 一些判断函数
//判断字符是否为数字
int isnumber(char c)
{
return c>='0' && c<='9';
}
//判断是否为左括号
int isleft(char c)
{
return c=='(';
}
//判断是否为右括号
int isright(char c)
{
return c==')';
}
//判断是否为运算赋
int isoperator(char c)
{
return c=='+' || c=='-' || c=='*' || c=='/';
}
//判断运算符优先级
int getpriority(char c)
{
if (c=='*' || c=='/')
{
return 2;
}
if (c=='+' || c=='-')
{
return 1;
}
if (c=='(' || c==')')
{
return 0;
}
return -1;
}
3.3 按转换规则的实现代码
int main()
{
linkstack* stack = init_linkstack();
char str[] = "8 + (3 - 1) * 5";
for (int i = 0; i < sizeof(str) / sizeof(char); i++) //逐字符遍历str获得操作符;
{
my_data* data = new my_data;
data->node = NULL;
data->c = str[i];
if (isnumber(str[i])) //如果操作符为数字,直接输出
{
cout << str[i] << "\t";
}
if (isleft(str[i])) //如果操作符为左括号,直接进栈
{
push_linkstack(stack, (linknode*)data);
}
if (isright(str[i])) //如果操作符为右括号从栈里往外弹元素直到弹出左括号为止
{
while (stack->size > 0)
{
char* c = &((my_data*)top_linkstack(stack))->c;
if (isleft(*c)) //匹配到左括号弹出
{
pop_linkstack(stack);
break;
}
//匹配到运算符,打印运算符并弹出运算符
cout << *c << "\t";
pop_linkstack(stack);
}
}
//如果操作符是运算符
if (isoperator(str[i]))
{
if (stack->size == 0) //如果栈为空,操作符直接入栈
{
push_linkstack(stack, (linknode*)data);
}
else //不是空栈则需要进行优先级比较
{
while (stack->size > 0) //操作符与栈中元素符号优先级比较
{
char* c = &((my_data*)top_linkstack(stack))->c; //栈顶元素符号
if (getpriority(data->c) > getpriority(*c)) //操作符符优先级高于栈中top元素符号,操作符入栈
{
push_linkstack(stack, (linknode*)data);
break;
}
if (getpriority(data->c) <= getpriority(*c)) //操作符优先级低于或等于栈中top元素符号,并打印并弹出栈中top元素
{
cout << ((my_data*)top_linkstack(stack))->c << "\t";
pop_linkstack(stack);
if (stack->size == 0) //弹出top元素后栈为空,操作符直接入栈
{
push_linkstack(stack, (linknode*)data);
break;
}
}
}
}
}
}
//如果str遍历完了,但栈中还有元素符号,将其逐个输出,直到栈空为止
while (stack->size > 0)
{
cout << ((my_data*)top_linkstack(stack))->c << "\t";
pop_linkstack(stack);
}
cout << endl;
system("pause");
return 0;
}
3.4 运行结果

可以看到运行结果是与上面我们的预期一致的。
3.5 整体代码
#include<iostream>
using namespace std;
// 有关栈的基本操作
//节点
class linknode
{
public:
linknode* next;
};
//自定义数据
class my_data
{
public:
linknode* node;
char c;
};
//链式栈
class linkstack
{
public:
linknode head;
int size;
};
//初始化栈
linkstack* init_linkstack()
{
linkstack* stack = new linkstack;
stack->head.next = NULL;
stack->size = 0;
return stack;
}
//入栈
void push_linkstack(linkstack* stack, linknode* data)
{
data->next = stack->head.next;
stack->head.next = data;
stack->size++;
}
//出栈
void pop_linkstack(linkstack* stack)
{
stack->head.next = stack->head.next->next;
stack->size--;
}
//返回栈顶元素
linknode* top_linkstack(linkstack* stack)
{
return stack->head.next;
}
//判断字符是否为数字
int isnumber(char c)
{
return c >= '0' && c <= '9';
}
//判断是否为左括号
int isleft(char c)
{
return c == '(';
}
//判断是否为右括号
int isright(char c)
{
return c == ')';
}
//判断是否为运算赋
int isoperator(char c)
{
return c == '+' || c == '-' || c == '*' || c == '/';
}
//判断运算符优先级
int getpriority(char c)
{
if (c == '*' || c == '/')
{
return 2;
}
if (c == '+' || c == '-')
{
return 1;
}
if (c == '(' || c == ')')
{
return 0;
}
return -1;
}
int main()
{
linkstack* stack = init_linkstack();
char str[] = "8 + (3 - 1) * 5";
for (int i = 0; i < sizeof(str) / sizeof(char); i++) //逐字符遍历str获得操作符;
{
my_data* data = new my_data;
data->node = NULL;
data->c = str[i];
if (isnumber(str[i])) //如果操作符为数字,直接输出
{
cout << str[i] << "\t";
}
if (isleft(str[i])) //如果操作符为左括号,直接进栈
{
push_linkstack(stack, (linknode*)data);
}
if (isright(str[i])) //如果操作符为右括号从栈里往外弹元素直到弹出左括号为止
{
while (stack->size > 0)
{
char* c = &((my_data*)top_linkstack(stack))->c;
if (isleft(*c)) //匹配到左括号弹出
{
pop_linkstack(stack);
break;
}
//匹配到运算符,打印运算符并弹出运算符
cout << *c << "\t";
pop_linkstack(stack);
}
}
//如果操作符是运算符
if (isoperator(str[i]))
{
if (stack->size == 0) //如果栈为空,操作符直接入栈
{
push_linkstack(stack, (linknode*)data);
}
else //不是空栈则需要进行优先级比较
{
while (stack->size > 0) //操作符与栈中元素符号优先级比较
{
char* c = &((my_data*)top_linkstack(stack))->c; //栈顶元素符号
if (getpriority(data->c) > getpriority(*c)) //操作符符优先级高于栈中top元素符号,操作符入栈
{
push_linkstack(stack, (linknode*)data);
break;
}
if (getpriority(data->c) <= getpriority(*c)) //操作符优先级低于或等于栈中top元素符号,并打印并弹出栈中top元素
{
cout << ((my_data*)top_linkstack(stack))->c << "\t";
pop_linkstack(stack);
if (stack->size == 0) //弹出top元素后栈为空,操作符直接入栈
{
push_linkstack(stack, (linknode*)data);
break;
}
}
}
}
}
}
//如果str遍历完了,但栈中还有元素符号,将其逐个输出,直到栈空为止
while (stack->size > 0)
{
cout << ((my_data*)top_linkstack(stack))->c << "\t";
pop_linkstack(stack);
}
cout << endl;
system("pause");
return 0;
}