前言
姜老师是一个好老师,编译原理没有过是我的问题,我爱姜老师。
写这篇博客涉及到好多符号,可以参考这篇文章latex数学公式详细教程
因为打字过于麻烦,很多内容用平板的手写截图,还有电脑截图替代,不太习惯用平板写字,也不太习惯用鼠标写字,所以写地歪歪扭扭略有凌乱,各位见谅。
1. 编译概述
1.1 翻译程序
翻译程序:把某种程序设计语言(源语言)编写的程序(源程序)翻译成与之等价的另一种语言(目标语言)的程序(目标程序)。
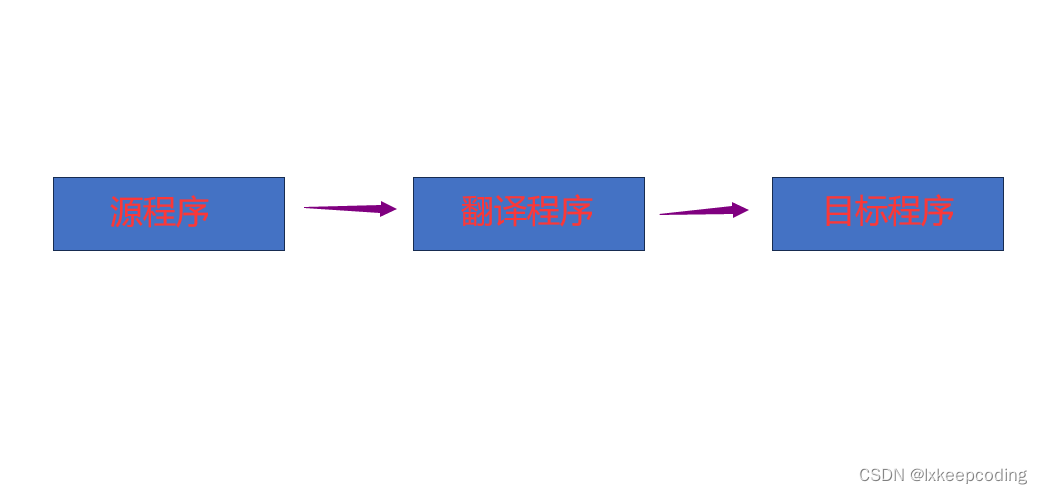
编译程序:编译程序是一种翻译程序,将高级语言编写的源程序翻译成等价的机器语言或汇编语言的目标程序。
解释程序:翻译一句执行一句,不生成目标文件,直接执行源代码文件。
1.2 编译过程和编译程序的基本结构
- 编译程序的几个工作阶段
词法分析
语法分析
语义分析
中间代码生成
代码优化
目标代码生成
2. 文法与语言
2.1 符号串与语言
-
字母表:大写字母表示,或Σ(A={0,1} Σ=(a,b,c,d))
有穷非空集合(C语言的字母表:ASSIC) -
符号:Σ中的元素
-
符号串:Σ中符号的序列
-
长度:符号串中元素个数 记为|x|
-
空串:长度为0,记为ϵ , |ϵ|=0
-
运算:符号串的连接,把y写在x后面,记为xy
显然:
a. ϵx=x=ϵx
b. |xy|=|x|+|y| -
头尾子串
符号串Σ=xyw
x为头,w为尾
Σ=x……
Σ=……w
Σ=……y……
x=ab,子串:a,b,ab,ϵ,头:a,ab,ϵ -
符号串的方幂
x为串,xxxx……x(n个x)记为xn
显然:
a. xn=|x|+|x|+|x|+……+|x| n个|x|
b. xn xm=xn+m =xm+n=xm xn
c. |x0 |=0 , |ϵ|=0,x0=ϵ -
符号串的集合 -->就是语言
Σ串是符号串构成的集合,用大写字母表示(A,B……) -
集合中元素个数 记为|A|
-
空集 ϕ \phi ϕ | ϕ \phi ϕ|=0
注意:区别 ϕ \phi ϕ、{ϵ}和 ξ \xi ξ ,|ϵ|=1,| ϕ \phi ϕ|=0 -
运算
符号串集合 A和B的乘积 A ⋅ \cdot ⋅B={xy|x ∈ \in ∈ A,且y ∈ \in ∈ B}
A={0,1},B={a,b}
A ⋅ \cdot ⋅B ={0a,0b,1a,1b}
显然:
a.|AB|=|A| ⋅ \cdot ⋅|B|
(重复元素重复计算)
b. ϕ \phi ϕA=0=| ϕ \phi ϕ |= A ϕ \phi ϕ
{ϵ}A=A=A{ϵ}
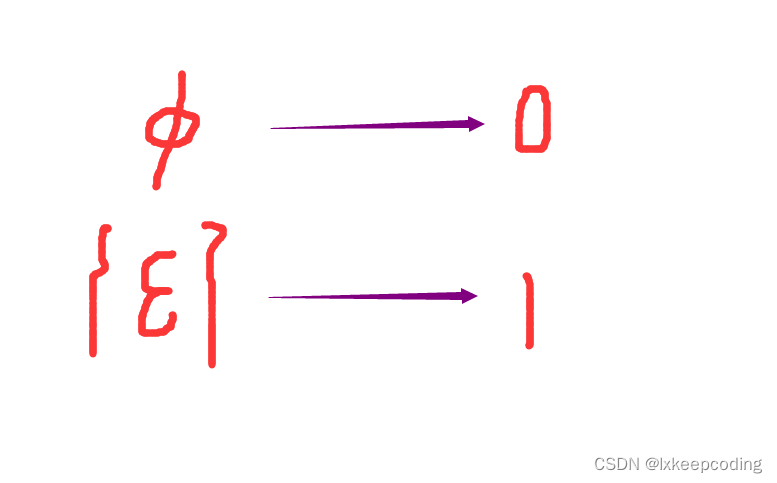
-
符号串集合的方幂
AAAAA……A (n个A)
Σ={0,1}
Σ1={0,1}
Σ2={00,01,10,11}
……
Σn=Σ字母表中所有长度为n的符号串构成的集合
显然:
a. AnAm=An+m=Am+n=AmAn
b. |An|=(|A|)n
c. A0={ϵ} -
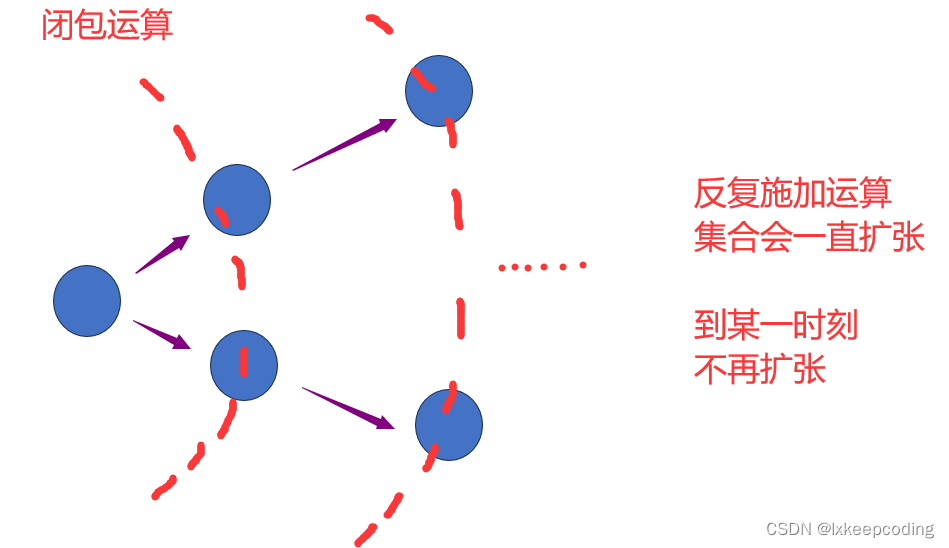
正闭包+和闭包*
设A为符号串集合
A+=A1 ∪ \cup ∪A2 ∪ \cup ∪A3 ……
A*=A0 ∪ \cup ∪ A1 ∪ \cup ∪A2 ∪ \cup ∪A3 ……
Σ+ ={所有长度≥1的串}
Σ* ={Σ上任意串}
显然:
a. A+ =AA*
b. (A* )* =A*
-
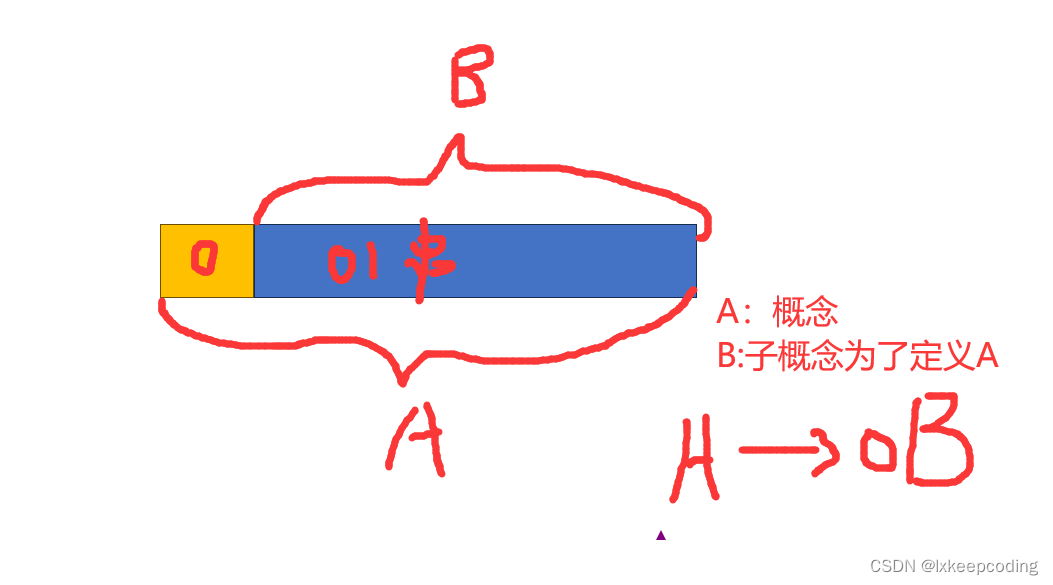
规则(产生式)
有序对(A, α \alpha α)
记为 A–> α \alpha α 或A::= α \alpha α
如:
A代表以0开头的有0,1组成的串A–> 0B
附:
非终结符:表示抽象概念,最终不出现 V
N
_N
N
终结符 :要写出来 V
T
_T
T
例:
被2整除的0,1构成的串
结构上:
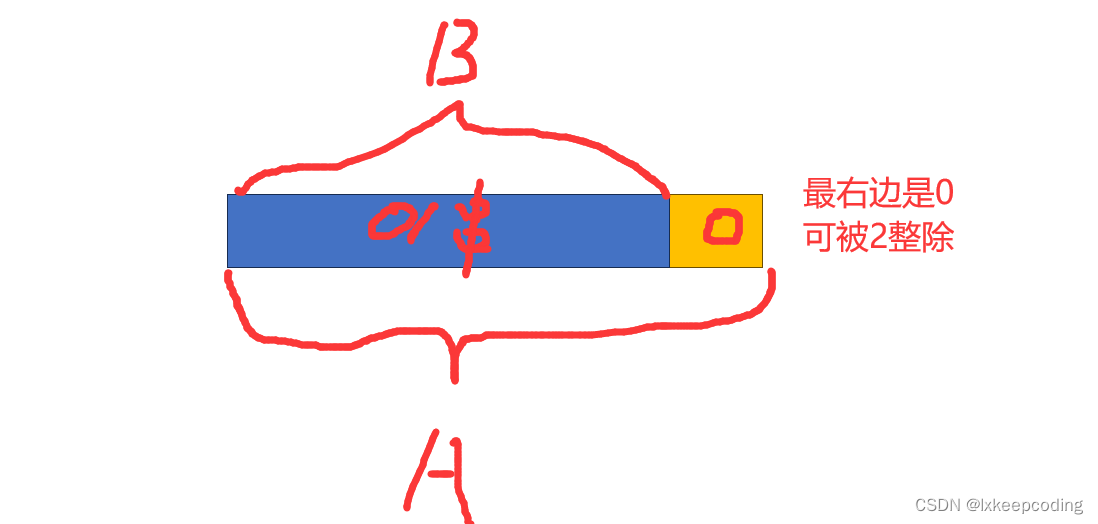
A–>B0
那么B又有哪些可能呢?
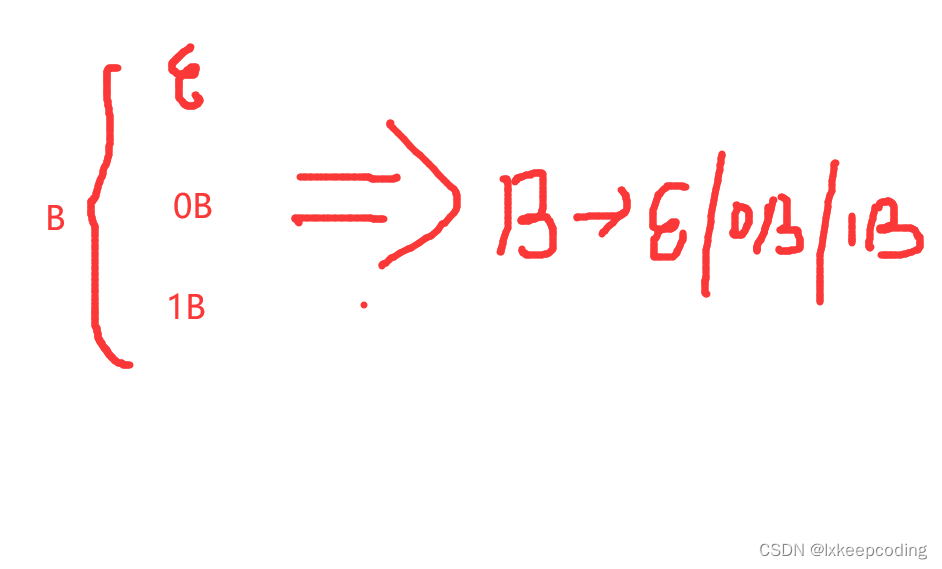
所以
A–>0B
B–>ϵ
B–>0B
B–>1B
(递归)
- 文法
文法G是四元组(V N _N N,V T _T T,P,Z)
V N _N N -----------非终结符,非空有穷
V T _T T------------终结符,非空有穷
P --------------规则的集合
Z--------------开始符号(最终关心要定义的那个非终结符)
G[Z] (V N _N N,V T _T T,P,Z)

给定一个问题设计一个相应的文法
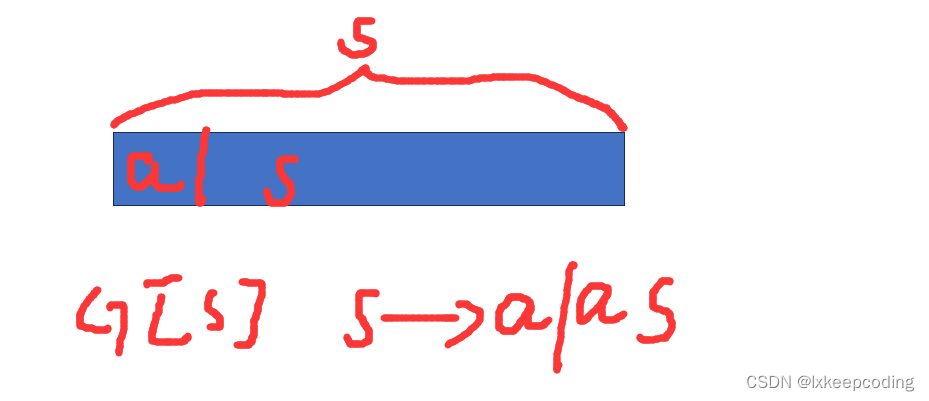
例1,设计G表达{an |a>=1}
第一种方法,归纳法(生成法)

第二种方法:分析法
例2,设计一个文法G表示{an bm |m,n>=1}

例3,设计一个G表示{an bn |n>=1}
(配对)

附:什么是直接推导?
设
α
\alpha
αAB串,A–>
γ
\gamma
γ
α
\alpha
αAB中A用
γ
\gamma
γ 代替
α
\alpha
α
γ
\gamma
γB

例4,设计一个文法G表示{an bn cm |m,n>=1}

例5,设计一个语法G表示{an bm cn|m,n>=1}

例6,被2整除的0,1串

例7,被三整除的0,1串

- 认识一些推导

例:

-
最左、最右、规范推导
最左(最右)推导:指一个推导序列中,每一步直接推导 α \alpha α ⇒ \Rightarrow ⇒ β \beta β
都是对 α \alpha α 中的最左(最右)非终结符进行替换。
在形式语言中,最右推导通常称为规范推导。
规范推导的逆过程称为最左规约,也称为规范规约。

-
语法树
推导过程用树表示出来。
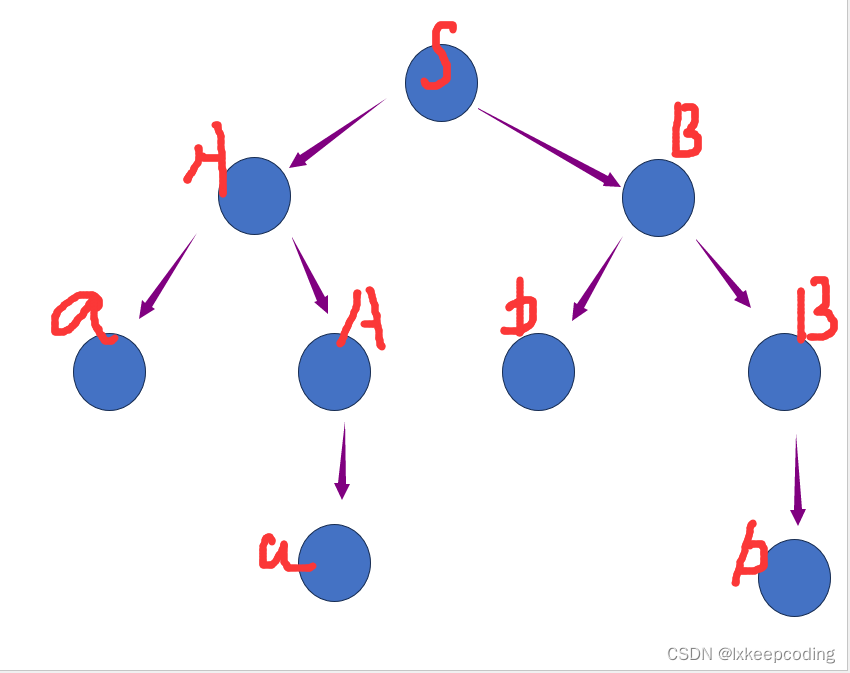
-
文法的二义性
如果一个文法存在某个句子具有两棵不同的语法树,则称这个语法是二义的。 -
句型,句子,语言
句子本身属于句型,句子所有符号都是终结符
语言,G【s】所确定的语言为L(G[S])
一个文法决定一个语言
2.2 文法的左递归

2.3 短语、直接短语、句柄
直接短语

看一个例子

首先画出语法树
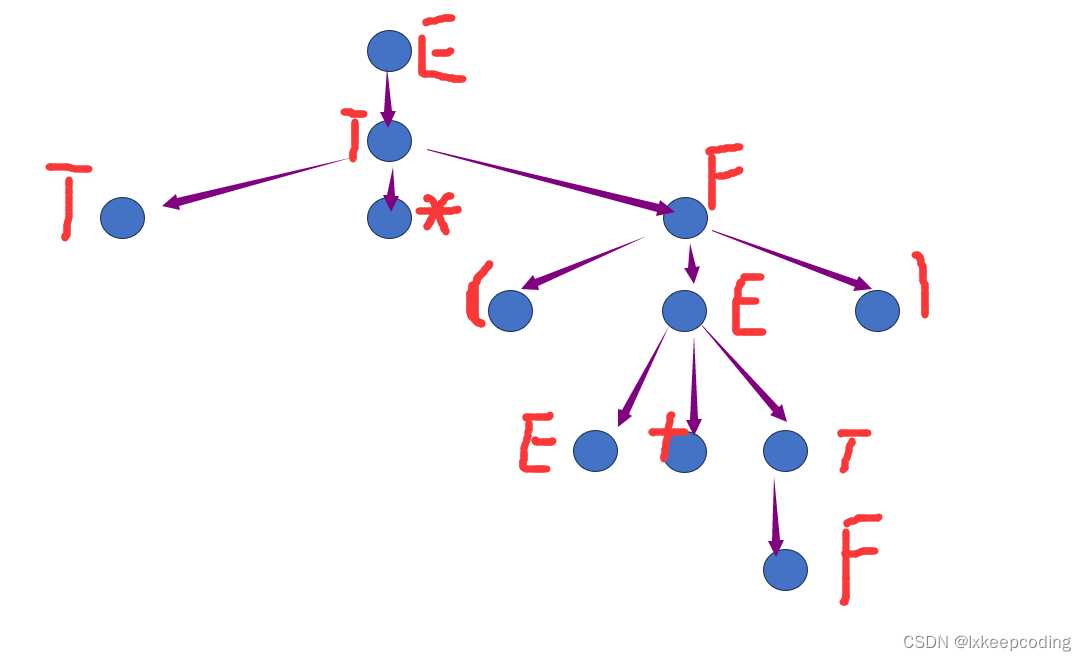
短语:语法树中每一个内部结点包含树根都对应一个短语,所有叶子从左到右写出来。

直接短语:父子两代,直接长成的,一步生长
F……T
F……T
句柄:
F……T
(最左最小的树对应的符号串)
素短语:含有一个终结符,不含其他更小的素短语。
再来看一个例子:

2.4 文法的实用限制
1),不存在U–>U规则(直接删除)
2),每一个非终结符都是有用的
3),每一个非终结符都是能终止的
2.5 算法2.1:每一个非终结符都是有用的
有用留下,无用删除
打点法
初始化:集合U=V N _N N U中文法开始符号S打上标志
反复做:
对每一条规则,A–>
α
\alpha
α ,若A已打上标志,则
α
\alpha
α对应的所有的非终结符都是有用的,都打上标志一直做到集合U中没有新的符号打上标志。
最后:U中没有打上标志的符号,全部删除
来看一个例子:

2.6 算法2.2:每一个非终结符都能终止
前提:U–>
α
\alpha
α|
β
\beta
β 分开
U–>
α
\alpha
α
U–>
β
\beta
β
打点法
初始化:如果规则右部分全部由V
T
_T
T 符号组成,该规则左部符号打上标志
反复做:
对每一条规则,如果规则右部由V
T
_T
T中的符号以及打上标志非终结符组成,该规则符号左部打上标志。
一直到没有规则打上标志。
最后:直接删除未打上标志的

算法2.1 算法2.2要反复多次迭代运行直到2.1 2.2都不发生变化。
2.7 形式语言分类
0型文法
1型文法(上下文有关)
2型文法(上下文无关)
3型文法(正则文法)
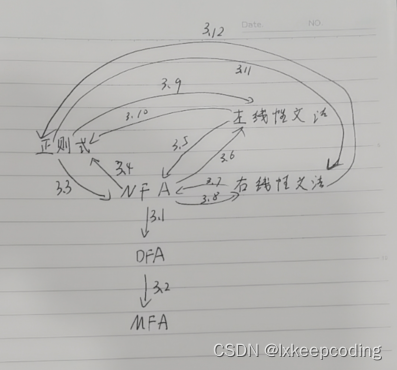
3. 词法分析
3.1 基本概念
- 功能
1),从组成源程序的字符串识别出一个单词(具有语法含义的最小单位)
2),依据词法规则识别单词
3),单词类别:保留字,标识符,常数,运算符,分隔符
4),单词的表示:二元组(类别,属性)
3.2 手工设计词法分析程序
3.3 有限自动机及其化简
3.3.1 NFA不确定有限自动机
M=(S,Σ, δ \delta δ,S 0 _0 0,F)
δ
\delta
δ:SXΣ* 到S子集映射
有空边一定是NFA,DFA是NFA的特例。
1),设计被2整除的0,1串
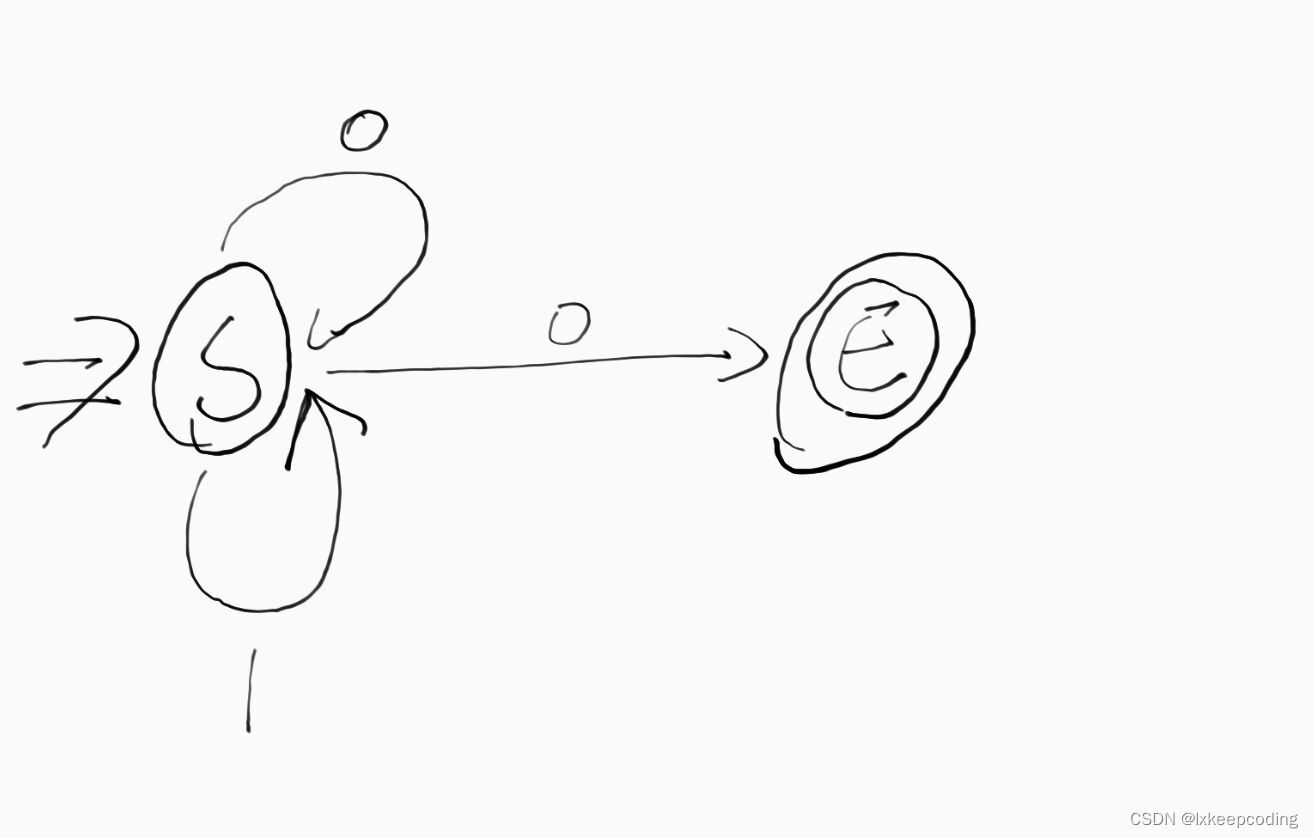
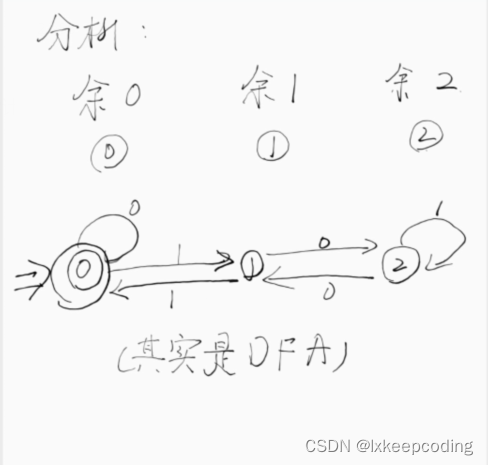
2),设计NFA,L(NFA)={被三整除的0,1串},
ξ
\xi
ξ也算
3.3.2 DFA确定的有限自动机
M=(S,Σ,
δ
\delta
δ,S
0
_0
0,F)
DFA只能允许一个开始状态
1),设计一个DFA表示L={以0开头的0,1串}
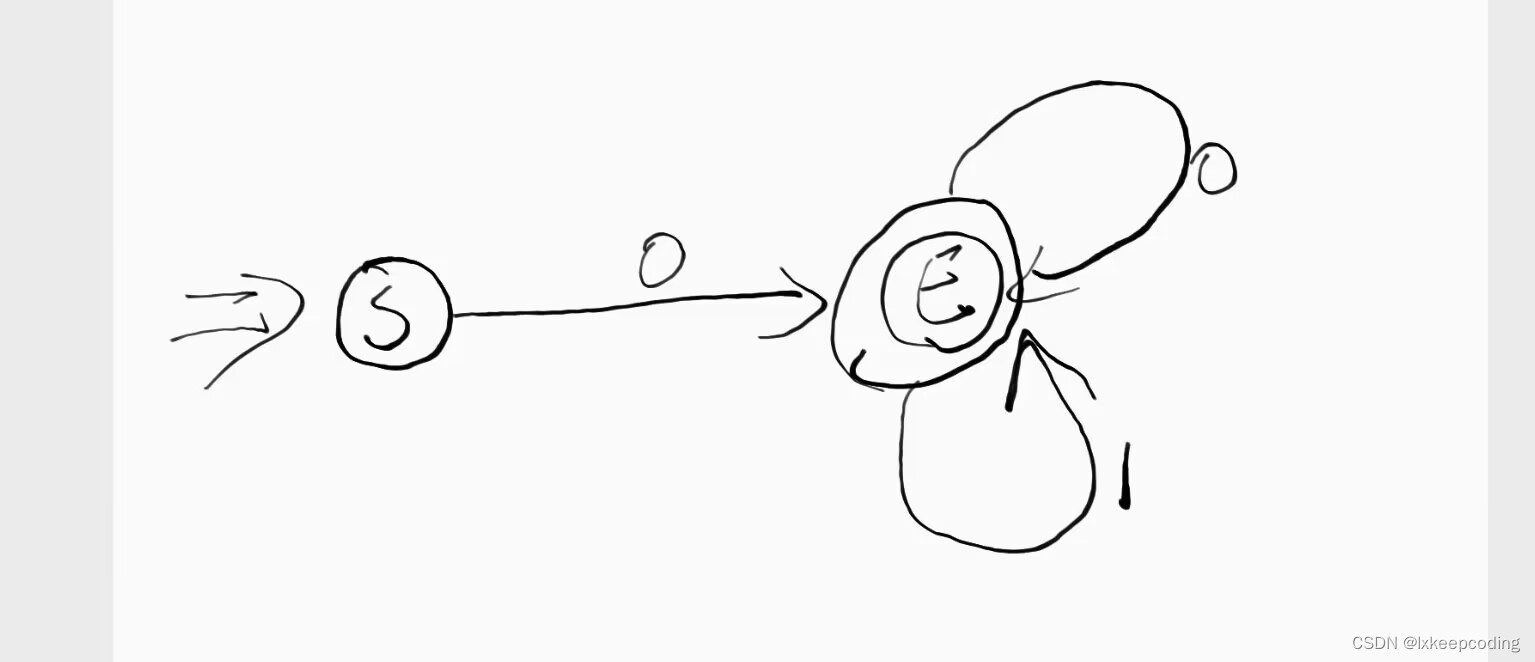
2),L(DFA)={ϵ}

3),L(DFA)= ϕ \phi ϕ

3.4 算法3.1 NFA的确定化(NFA–>DFA)
情形1:不存在ϵ边

1),请将下NFA化为DFA
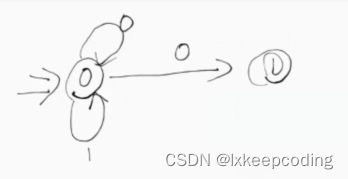
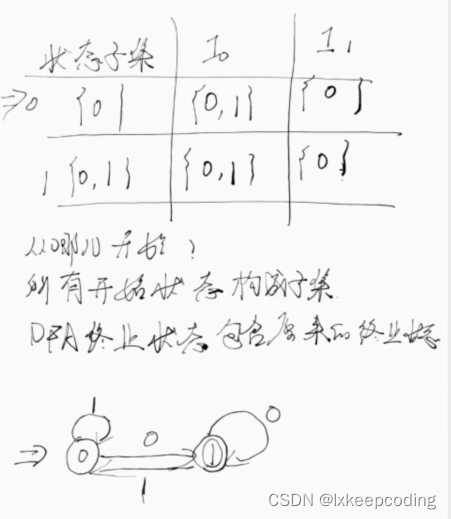
2),请将下NFA化为DFA
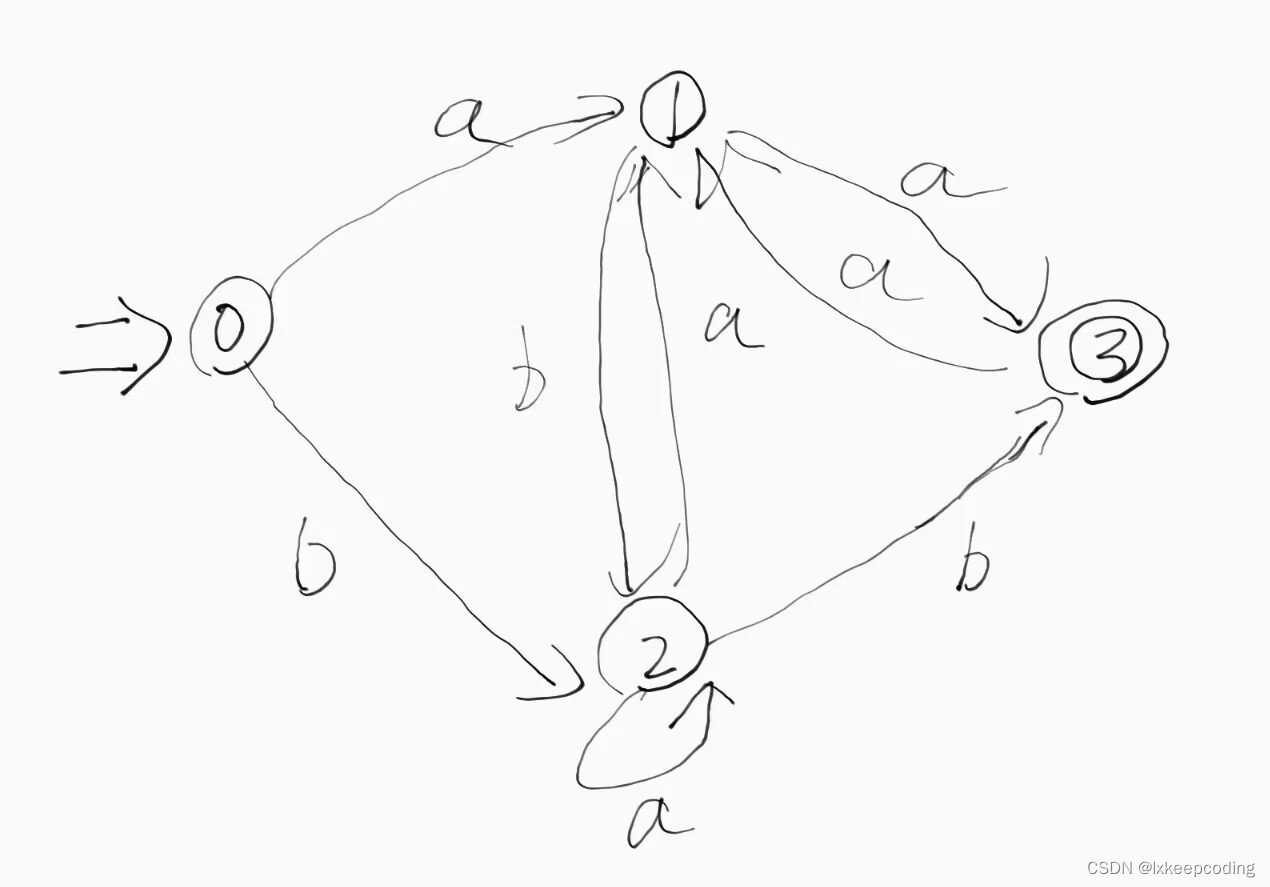

情形2:有
ϵ
\epsilon
ϵ边
ϵ
\epsilon
ϵ边的作用
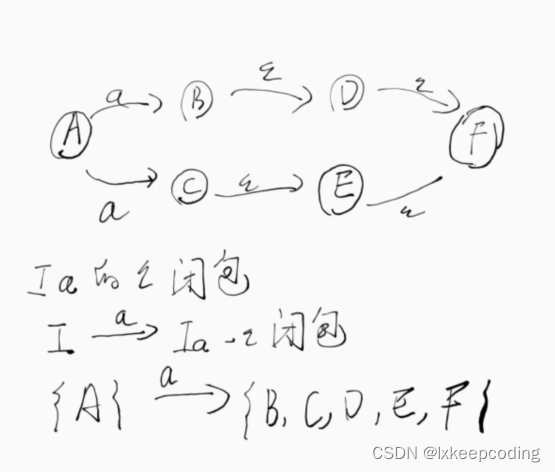
1),请将下NFA化为DFA
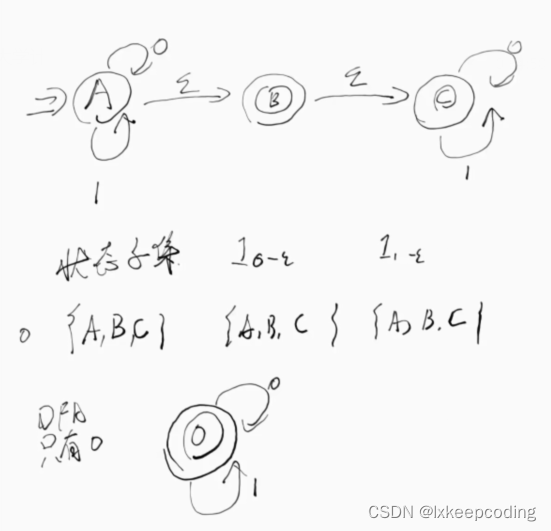
2),L={
ϵ
\epsilon
ϵ}设计一个NFA表示

结果如下
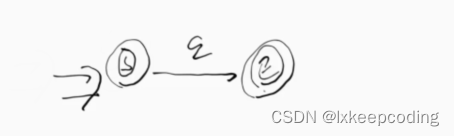
3),请将下NFA化为DFA
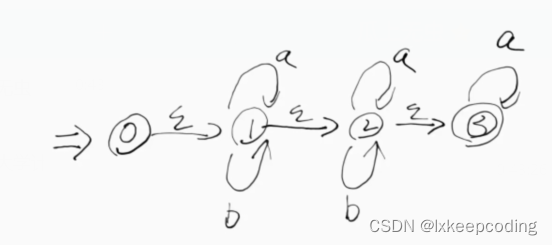

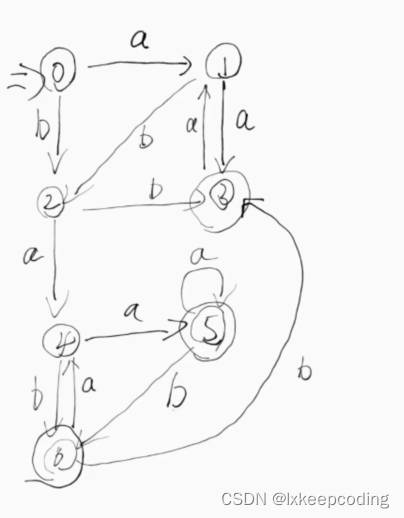
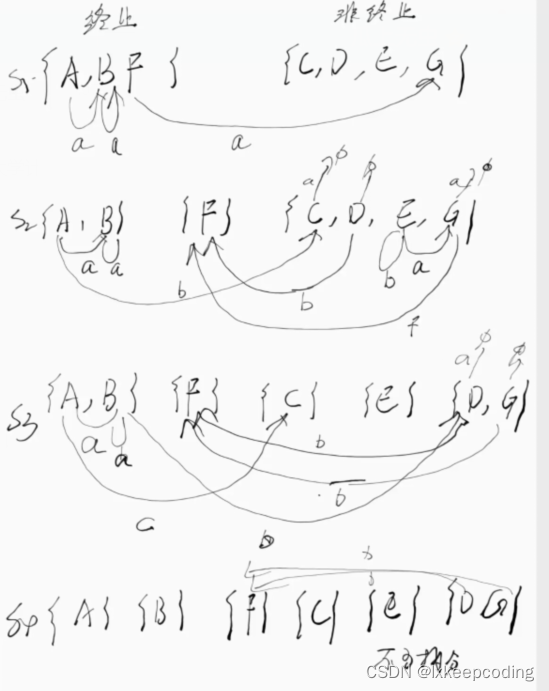
3.5 算法3.2 DFA的化简(DFA–>MFA)
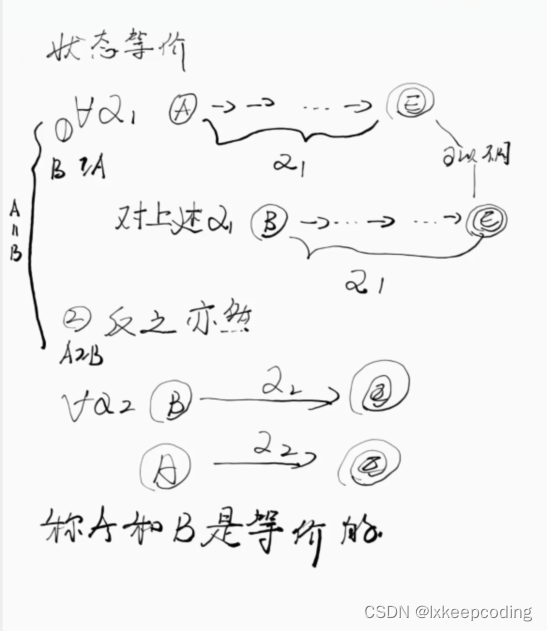

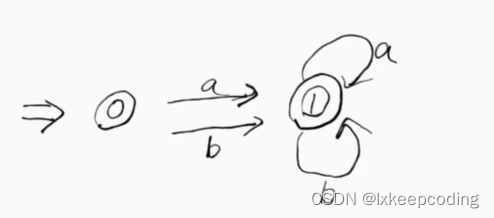
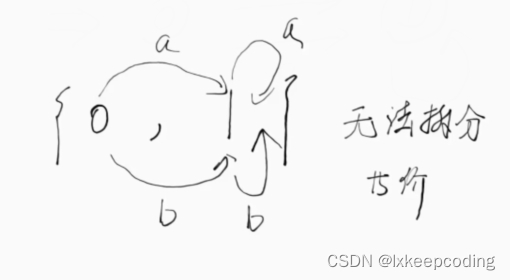
DFA的最优化,将不等价的状态拆分
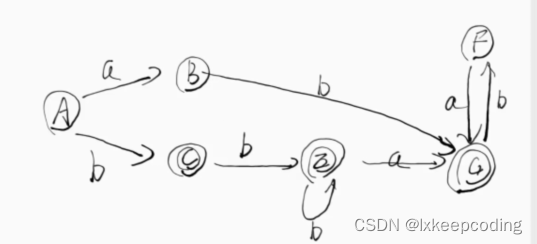
1),DFA–>MFA
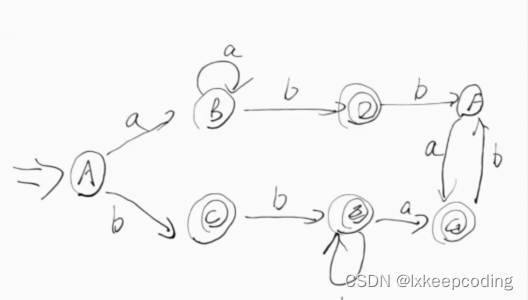
2), DFA–>MFA
3.6 正则式
正则式:以a开头后跟任意多个b,记为ab*
正则集:a,ab,abb,……
满足特征所有符号串构成的集合
核心运算定义

正则式的性质:

1),L(e)={任意0,1串}
(0|1)*
2),L(e)={以0开头0,1串}
0(0|1)*
3),L(e)={被2整除的0,1串}
(0|1)*0
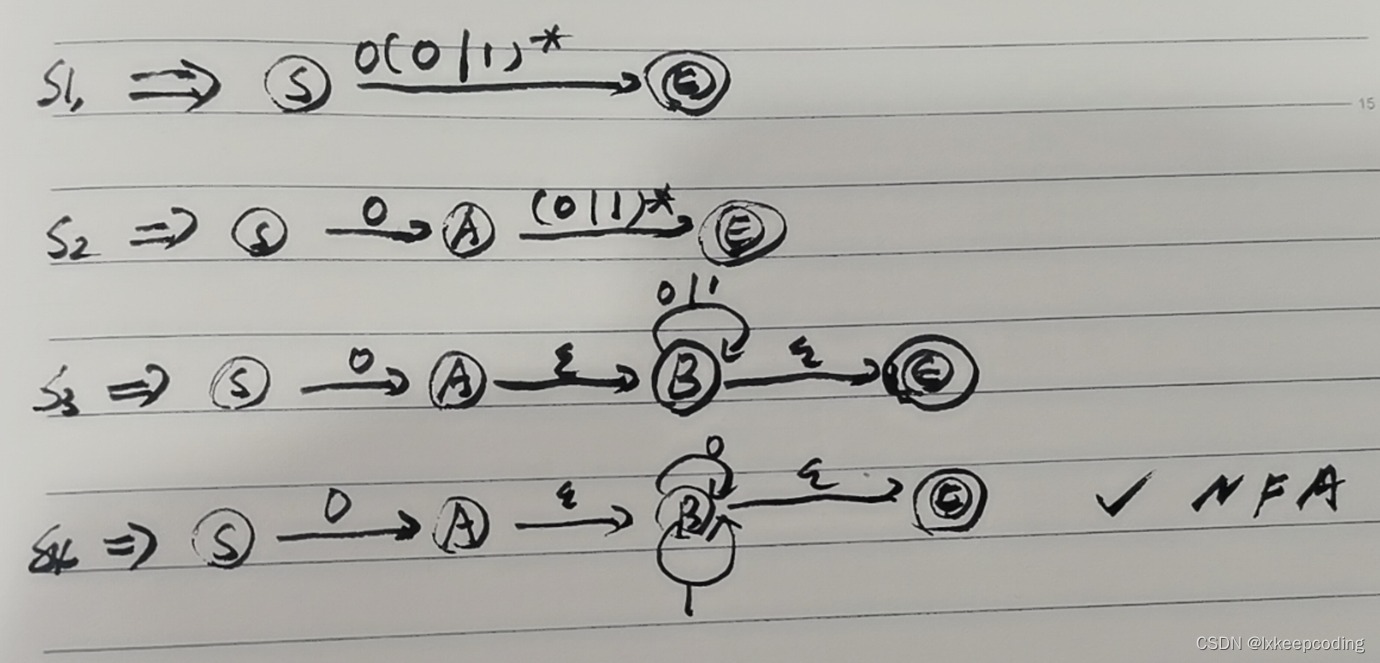
3.7 算法3.3 正则式–>NFA

1),0(0|1)*
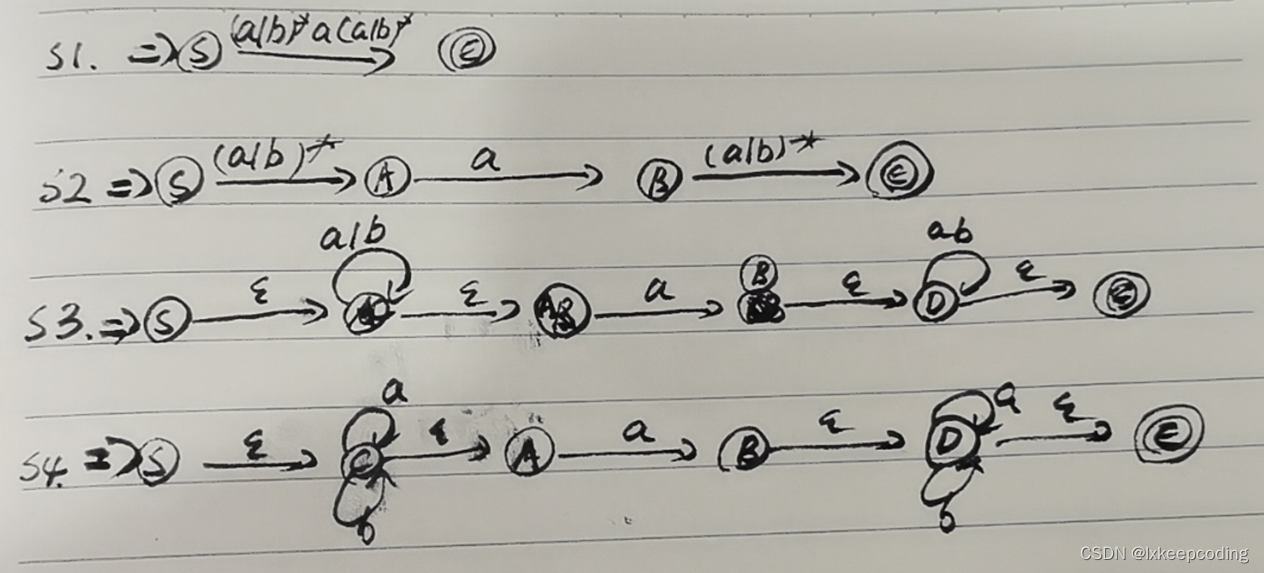
2),(a|b)* a (a|b)*
3.8 算法3.4 NFA–>正则式
改造NFA:
1)检查NFA是不是只有一个开始状态且发出边,否则引入一个新的开始状态且发出
ϵ
\epsilon
ϵ边,指向旧的开始状态。
2)检查NFA是否只有一个终止状态,只接受边,否则引入一个新的终止状态,旧的终止状态发出
ϵ
\epsilon
ϵ边指向它。
目标:唯一的开始,唯一的终止。
反复使用如下四条规则

1),被2整除的0,1串

2),被三整除的0,1串, ϵ \epsilon ϵ也算
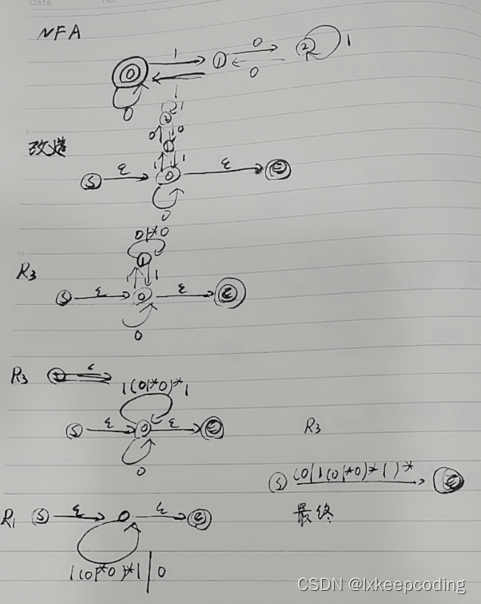
3.9 算法3.5 左线性文法–>NFA
左线性文法和右线性文法


1),左线性转换NFA
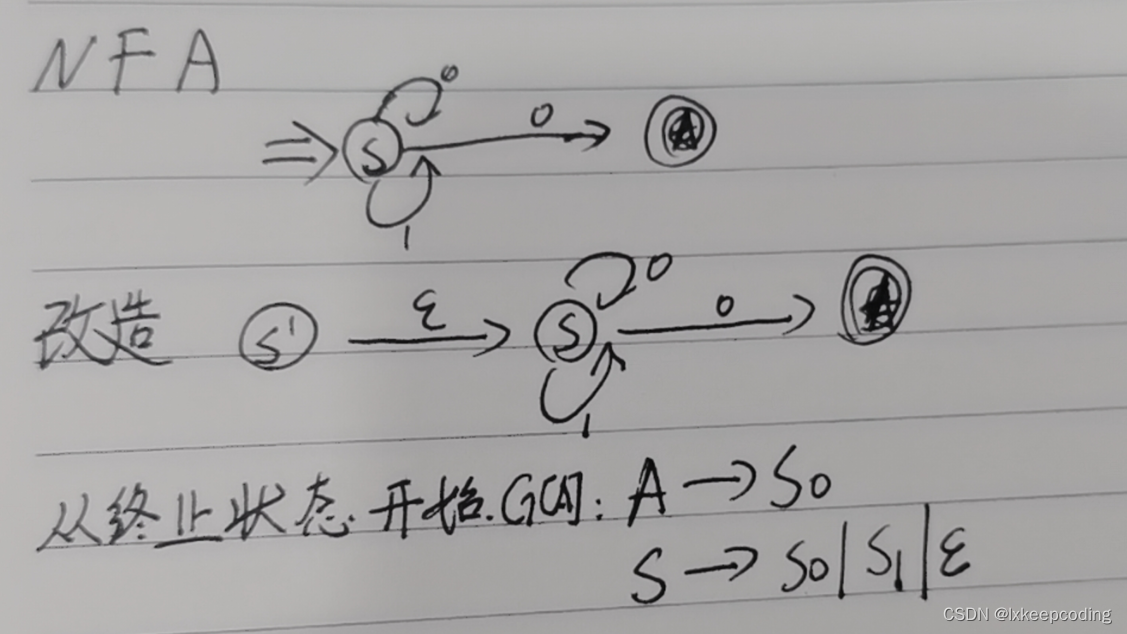
3.10 算法3.6 NFA–>左线性文法

1),被2整除的0,1串,NFA–>左线性文法
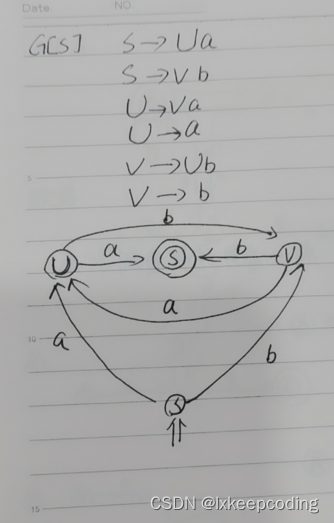
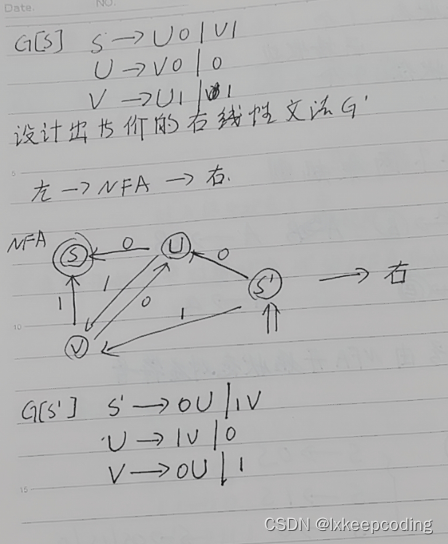
3.11 算法3.7 右线性文法–>NFA

1),右线性文法–>NFA
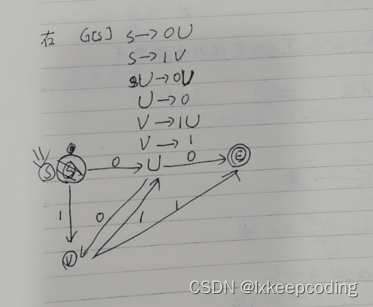
3.12 算法3.8 NFA–>右线性文法

1),NFA–>右线性文法

2),NFA–>右线性文法
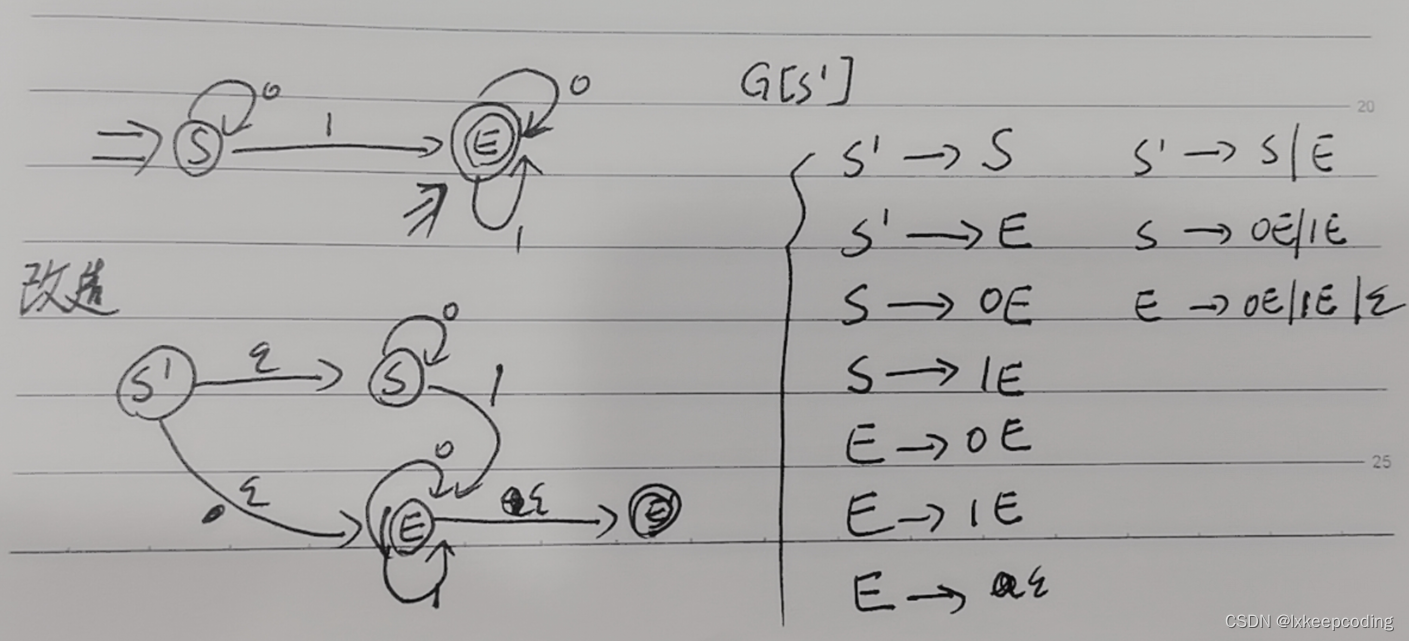
3),左线性文法改造为右线性文法
3.13 算法3.9 左线性文法–>正则表达式

1),左线性文法–>正则表达式

3.14 算法3.10 正则表达式–>左线性文法

1),正则表达式–>左线性文法

3.15 算法3.11 右线性文法–>正则表达式

1),右线性文法–>正则表达式

2),右线性文法–>正则表达式

3.16 算法3.12 正则表达式–>右线性文法

1),正则表达式–>右线性文法

3.17 12个算法的相互关系