【数据结构】堆

堆排序

如果只是将待排数组建立一个大堆或者小堆是无法得到一个升序或者降序的数组，因为对与一个堆，我们没法知道同一层的大小关系。

但是，如果建立了一个大堆，那么堆顶元素一定是这个数组中最大的，那么将堆顶元素删除（并不是真的删除，而是放在数组最后）用其余元素再次建立一个堆，那么这个新堆的堆顶元素就是剩余元素中的最大值，不断循环则个操作不就可以得到一个升序的数组。

• 升序建大堆
• 降序建小堆

降序排列为例

void swap(int* a, int* b)
{
	int temp = *a;
	*a = *b;
	*b = temp;
}

void sort(int a[], int n)
{
	for (int i = 1; i < n; i++)//建小堆
	{
		ShiftUp(a, n, i);
	}
	for (int j = 1; j < n; j++)
	{
		swap(&a[0], &a[n - j]);
		ShiftDown(a, n - j, 0);//每次将堆顶的元素（数组末端的交换值）向下移动重新建小堆
		
	}
}

Top-K问题

求数据结合中前K个最大的元素或者最小元素

求解思路

1. 将前k个元素建堆
   • 如果求最大就建小堆，如果求最小建大堆
2. 将剩余n-k个元素依次和堆顶元素比较，不满足某个条件就替换
   • 某个条件是：如果求前K个最大元素，则是堆顶元素小于剩余元素，如果求前K个最小元素，则是大于剩余元素

为什么求前K个最大的元素要建小堆

举一个简单的例子，在1,2，3,4，5,6，7中求前3个最大元素
首先前三个元素1,2，3建立一个小堆

4和小堆堆顶元素比较，替换堆顶元素1，重新建堆（2,4，3）

5和小堆堆顶元素比较，替换堆顶元素2，重新建堆（3,4，5）
6和小堆堆顶元素比较，替换堆顶元素3，重新建堆（4,6，5）
7和小堆堆顶元素比较，替换堆顶元素4，重新建堆（5,6，7）

替换的过程就是将原来堆中最小的元素剔除掉，换一个较大的元素进去，不断重复这个过程，这个堆中最小的元素越来越大，那么最后也只有第k大的元素可以替换掉这个堆中最小的元素，那么就求出了前K个最大的元素

以求前K个最大元素为例

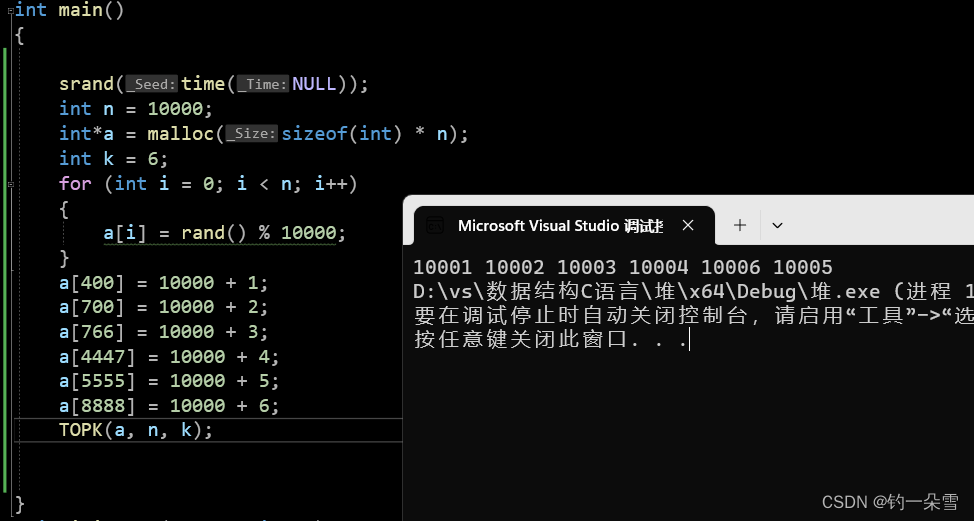
void TOPK(int*a,int n,int k)
{
	for (int i = (k - 1) / 2; i >= 0; i--)
	{
		ShiftDown(a, k, i);
	}
	for (int i = k; i < n; i++)
	{
		if (a[i] > a[0])
		{
			int temp = a[i];
			a[i] = a[0];
			a[0] = temp;
			for (int i = (k - 1) / 2; i >= 0; i--)
			{
				ShiftDown(a, k, i);
			}
		}
	}
	for (int i = 0; i < k; i++)
	{
		printf("%d ", a[i]);
	}
	
}