数据挖掘Java——Apriori算法的实现

news2024/9/21 12:38:37

一、Apriori算法的前置知识

Apriori算法是一种挖掘关联规则的频繁项集算法，其核心思想是通过候选集生成和向下封闭检测两个阶段来挖掘频繁项集。

关联规则挖掘是数据挖掘中最活跃的研究方法之一，最初的动机是针对购物篮分析问题提出的，其目的是为了发现交易数据库中不同商品之间的练习规则。通过用户给定的最小支持度，寻找所有频繁项目集，即满足Support不小于Minsupport的所有项目子集。通过用户给定的最小可信度，在每个最大频繁项目集中，寻找Confidence不小于Minconfidence的关联规则。

支持度：支持度就是几个关联的数据在数据集中出现的次数占总数据集的比重。或者说几个数据关联出现的概率。

置信度：置信度体现了一个数据出现后，另一个数据出现的概率，或者说数据的条件概率。

二、Apriori算法的基本思想

首先扫描数据库中所需要进行分析的数据，在设置完支持度以及置信度以后，在最小支持度的支持下产生频繁项，即统计所有项目集中包含一个或一个以上的元素频数，找出大于或者等于设置的支持度的项目集。其次就是频繁项的自连接。再者是如果对频繁项自连接以后的项的子集如果不是频繁项的话，则进行剪枝处理。接着对频繁项处理后产生候选项。最后循环调用产生频繁项集。

三、Apriori算法和强关联规则挖掘的例子

Apriori算法例子
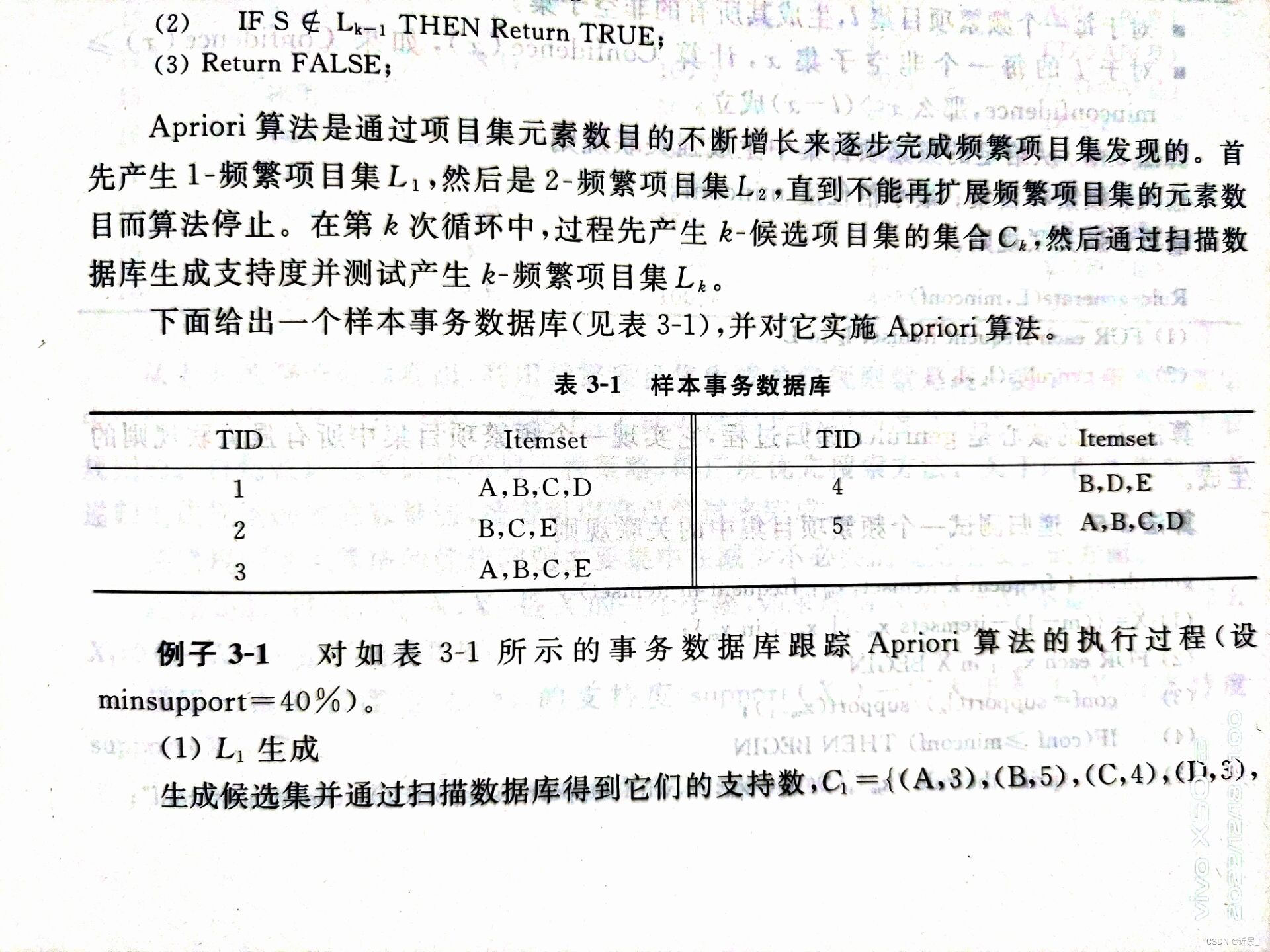
在这里插入图片描述
在这里插入图片描述

挖掘强关联规则的算法例子
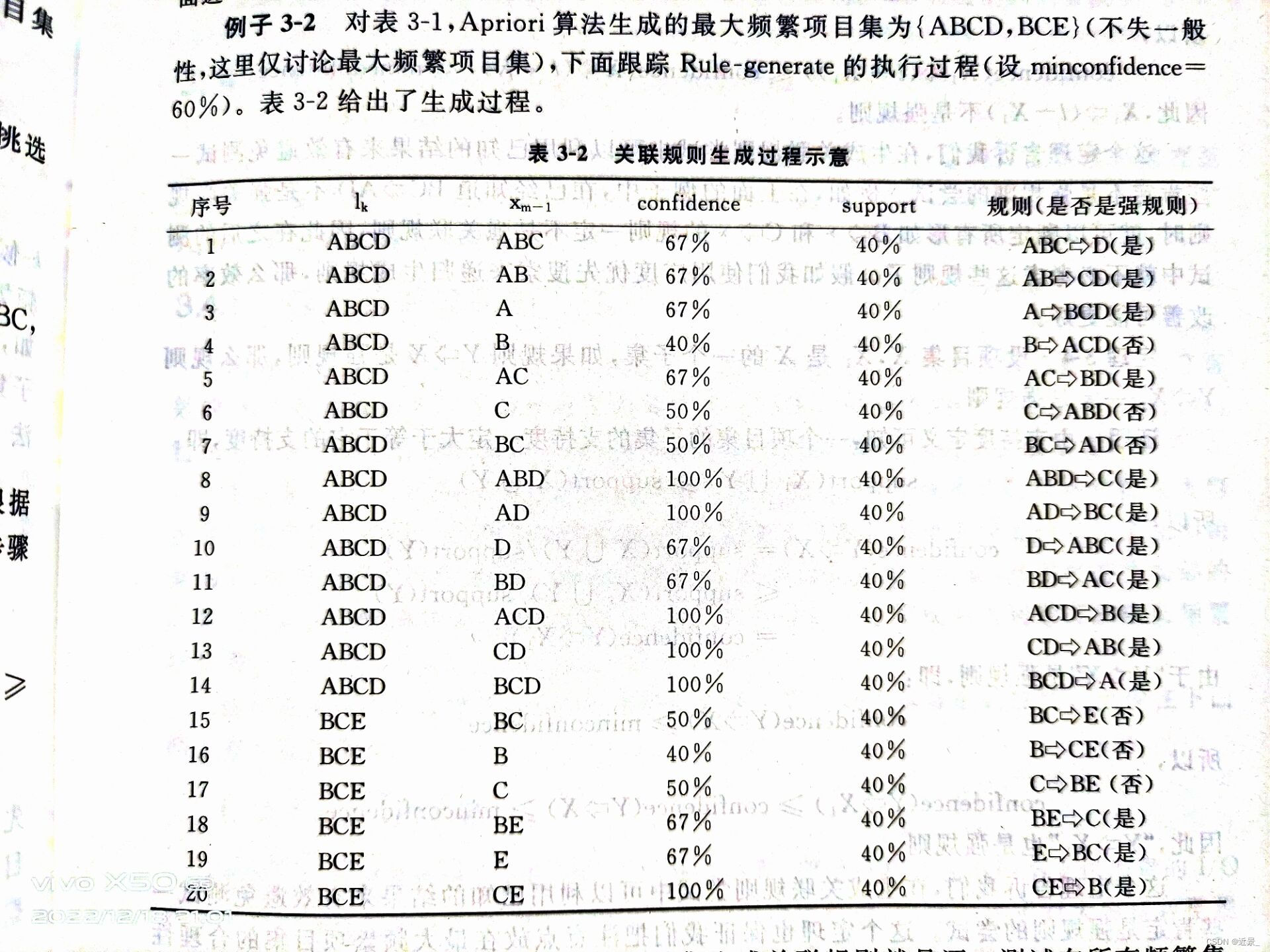
在这里插入图片描述

四、Apriori算法的实现过程

实验内容
有如下的交易记录，请编写程序实现Apriori算法，挖掘该交易记录里的频繁项集，并挖掘出所有的强关联规则，设最小支持度为50%，最小置信度为50%：
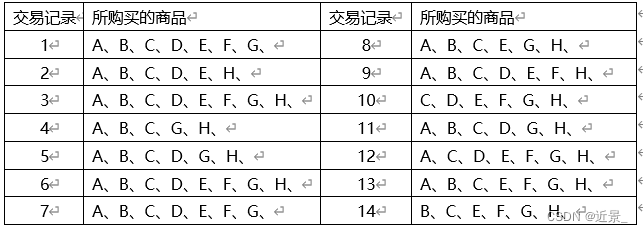
在这里插入图片描述

实验思路
（1）定义数据集、最小支持度、最小支持数、最小置信度以及存放所有频繁项目集的Map集合。调用就封装好的initDataList()方法对数据进行初始化。
（2）调用getAllElement()方法获取到数据集所含有的所有类别元素allElement，将allElement数组进行排列组合获取候选集candidateL1。调用getItemSets()方法遍历candidateL1，将出现次数不小于最小支持数minSupportCount的项加入到itemSets中，遍历结束，获取到1-频繁项目集L1，并将L1打印输出。
（3）开始循环找k-频繁项目集，直到得到的k-频繁项目集Lk为空，跳出循环。在循环体内部，将k-1-候选集candidateLast所含有的所有类别元素allElementLast作为参数调用getCombination()方法，获取k-候选集candidateNow，遍历k-候选集，将出现次数不小于最小支持数的项加入到itemSets并返回，得到频繁项目集Lk。如果k-频繁项集为空，则结束循环，若Lk不为空，则将Lk加入到存放所有频繁项目集allItemSets的集合中，方便之后找强关联规则。
（4）调用correlation()方法进行强关联规则的挖掘。在方法体内部，遍历所有的频繁项目集，得到每一项频繁项目集的非空子集集合subSet，遍历每一项频繁项目集的非空子集，以此非空子集和此频繁项目集作为参数，调用isConfidence()方法判断是否满足置信度大于最小置信度，若满足，则输出此非空子集==>非空子集的补集。

实现源码

package com.data.mining.main;

import com.google.common.collect.ArrayListMultimap;
import com.google.common.collect.Multimap;
import org.paukov.combinatorics3.Generator;
import org.paukov.combinatorics3.IGenerator;

import java.util.*;

public class Apriori {

    //定义单行数据
    public static String[] item1,item2,item3,item4,item5,item6,item7,item8,item9,item10,item11,item12,item13,item14;
    //定义数据集
    public static List<String[]> dataList = new ArrayList<>();
    //定义最小支持度
    public static double minSupport = 0.5;
    //定义最小支持数
    public static double minSupportCount = 0.0;
    //定义最小置信度
    public static double minConfidence = 0.5;
    //存放所有频繁项目集
    public static Map<Integer, Multimap<Integer, String[]>> allItemSets = new HashMap<>();

    public static void main(String[] args) {
        // 初始化数据集
        initDataList();
        String[] allElement = getAllElement(dataList);
        //获取候选集L1
        List<String[]> candidateL1 = getCombination(allElement, 1);
        Multimap<Integer, String[]> itemSetsL1 = getItemSets(candidateL1);
        allItemSets.put(1, itemSetsL1);

        printResult(itemSetsL1, 1);

        List<List<String[]>> stack = new ArrayList<>();
        stack.add(candidateL1);
        for (int k = 2; true; k++) {
            List<String[]> candidateLast = stack.get(0);
            String[] allElementLast = getAllElement(candidateLast);
            List<String[]> candidateNow = getCombination(allElementLast, k);
            Multimap<Integer, String[]> itemSetsLk = getItemSets(candidateNow);
            if (itemSetsLk.isEmpty()) break;
            allItemSets.put(k, itemSetsLk);
            printResult(itemSetsLk, k);
            stack.remove(0);
            stack.add(candidateNow);
        }
        correlation();
    }

    public static boolean isConfidence(String[] subSetStr1, String[] value){
        double confidence = getCountByConfidence(value) * 1.0 / getCountByConfidence(subSetStr1);
        if (confidence >= minConfidence) return true;
        return false;
    }

    public static Integer getCountByConfidence(String[] subSetStr){
        int count = 0; //存放子集在数据集中出现的次数
        for (String[] dataItem : dataList) {
            //比如在数据集第一项{A,B,C,D,E,F,G}中是否出现过A,B.C
            int index = -1;
            for (int i = 0; i < subSetStr.length; i++) {
                //比如A出现过，则index>0，若A没出现过，则index=-1
                index = Arrays.binarySearch(dataItem, subSetStr[i]);
                if (index < 0) break;
            }
            if (index >= 0){ //出现过ABC
                count++;
            }
        }
        return count;
    }

    /**
     * 找强关联规则
     */
    public static void correlation(){
        //遍历所有频繁项目集
        for (int k = 1; k <= allItemSets.size(); k++) {
            //获取k-频繁项目集
            Multimap<Integer, String[]> keyItemSet = allItemSets.get(k);
            Iterator<Map.Entry<Integer, String[]>> iterator = keyItemSet.entries().iterator();
            //遍历k频繁项目集
            while (iterator.hasNext()){
                Map.Entry<Integer, String[]> entry = iterator.next();
                String[] value = entry.getValue();
//                List<String> valueList = Arrays.asList(value);
//                List<String> valueList = new ArrayList<>();
//                Collections.addAll(valueList, value);
                //求value的非空子集
                for (int i = 1; i < value.length; i++) {
                    List<String[]> subSet = getCombination(value, i); //非空子集的集合
                    for (String[] subSetItem : subSet) { //subSetItm是频繁项目集每一个非空子集
                        List<String> valueList = new ArrayList<>();
                        Collections.addAll(valueList, value);
                        List<String> subSetItemList = Arrays.asList(subSetItem);
                        //去除已经求得子集后的valueList
                        valueList.removeAll(subSetItemList); //此时valueList中存放非空子集的补集
                        if (isConfidence(subSetItem, value)){
                            System.out.println(Arrays.toString(subSetItem) + "==>" + Arrays.toString(valueList.toArray(new String[valueList.size()])));
                        }
                    }
                }
            }
        }
    }

    /**
     * 打印出所有频繁项目集
     * @param itemSet
     * @param k
     */
    public static void printResult(Multimap<Integer, String[]> itemSet, int k){
        System.out.print("L" + k + "----------->");
        //使用迭代器遍历multimap
        Iterator<Map.Entry<Integer, String[]>> iterator = itemSet.entries().iterator();
        //遍历排列组合结果的每一项，将出现次数不小于minSupportCount的项加入到itemSets
        while (iterator.hasNext()){
            Map.Entry<Integer, String[]> entry = iterator.next();
//            System.out.println("key = " + entry.getKey() + "," + Arrays.toString(entry.getValue()));
            String[] value = entry.getValue();
            for (int i = 0; i < value.length; i++) {
                System.out.print(value[i]);
            }
            System.out.print(",");
        }
        System.out.println("");
//        System.out.println("-------------------------k=" + k + "-----------------------------------");
    }

    /**
     * 获取含有所有元素的数组
     * @param itemSet
     * @return
     */
    public static String[] getAllElement(List<String[]> itemSet){
        List<String> allElementList = new ArrayList<>(); //存放项目集中所有有的元素
        for (int i = 0; i < itemSet.size(); i++) {
            String[] item = itemSet.get(i);
            if (i == 0){ //将第一项的所有元素加入到allElementList中
                for (int j = 0; j < item.length; j++) {
                    allElementList.add(item[j]);
                }
            }else {
                for (int z = 0; z < item.length; z++) {
                    //判断allElementList中是否已经存在item[z]
                    int isExist = Arrays.binarySearch(allElementList.toArray(new String[allElementList.size()]), item[z]);
                    if (isExist < 0){ //不存在item[z]
                        allElementList.add(item[z]); //添加item[z]到allElementList中
                    }
                }
            }
        }
        return allElementList.toArray(new String[allElementList.size()]);
    }

    /**
     * 获取候选集
     * @param allItemStr 含频繁项目集所有元素的数组
     * @param k 要生成k候选集
     * @return
     */
    public static List<String[]> getCombination(String[] allItemStr, int k){
        //定义候选集
        List<String[]> candidateSets = new ArrayList<>();
        //对allItemStr进行k组合
        IGenerator<List<String>> candidateList = Generator.combination(allItemStr).simple(k);
        for (List<String> candidate : candidateList) {
            String[] candidateStr = candidate.toArray(new String[candidate.size()]);
            candidateSets.add(candidateStr);//将每一项组合放入候选集中
        }
        return candidateSets;
    }

    /**
     * 处理候选集，获取频繁项目集
     * @param itemList 候选集
     * @return 频繁项目集
     */
    public static Multimap<Integer, String[]> getItemSets(List<String[]> itemList){
        Multimap<Integer, String[]> itemSets = ArrayListMultimap.create(); //项目集
        //得到排列组合结果（候选集）每一项在数据集中出现的次数
        Multimap<Integer, String[]> itemCount = getItemCount(itemList);
        //使用迭代器遍历multimap
        Iterator<Map.Entry<Integer, String[]>> iterator = itemCount.entries().iterator();
        //遍历排列组合结果的每一项，将出现次数不小于minSupportCount的项加入到itemSets
        while (iterator.hasNext()){
            Map.Entry<Integer, String[]> entry = iterator.next();
            if (entry.getKey() >= minSupportCount){
                itemSets.put(entry.getKey(), entry.getValue());
            }
        }
        return itemSets;
    }

    /**
     * 获取排列组合结果（候选集）每一项在数据集中出现的次数
     * @param itemList
     * @return
     */
    public static Multimap<Integer, String[]> getItemCount(List<String[]> itemList){
        Multimap<Integer, String[]> itemCount = ArrayListMultimap.create();
        //遍历项目集
        for (String[] item : itemList) {
            int count = 0; //存放A,B.C在数据集中出现的次数
            for (String[] dataItem : dataList) {
                //比如在数据集第一项{A,B,C,D,E,F,G}中是否出现过A,B.C
                int index = -1;
                for (int i = 0; i < item.length; i++) {
                    //比如A出现过，则index>0，若A没出现过，则index=-1
                    index = Arrays.binarySearch(dataItem, item[i]);
                    if (index < 0) break;
                }
                if (index >= 0){ //出现过ABC
                    count++;
                }
            }
            itemCount.put(count, item); //存放(ABC出现的次数，{A,B,C})
        }
        return itemCount;
    }

    /**
     * 初始化数据集
     */
    public static void initDataList(){
        //初始化单行数据
        item1 = new String[]{"A", "B", "C", "D", "E", "F", "G"};
        item2 = new String[]{"A", "B", "C", "D", "E", "H"};
        item3 = new String[]{"A", "B", "C", "D", "E", "F", "G", "H"};
        item4 = new String[]{"A", "B", "C", "G", "H"};
        item5 = new String[]{"A", "B", "C", "D", "G", "H"};
        item6 = new String[]{"A", "B", "C", "D", "E", "F", "G", "H"};
        item7 = new String[]{"A", "B", "C", "D", "E", "F", "G"};
        item8 = new String[]{"A", "B", "C", "E", "G", "H"};
        item9 = new String[]{"A", "B", "C", "D", "E", "F", "H"};
        item10 = new String[]{"C", "D", "E", "F", "G", "H"};
        item11 = new String[]{"A", "B", "C", "D", "G", "H"};
        item12 = new String[]{"A", "C", "D", "E", "F", "G", "H"};
        item13 = new String[]{"A", "B", "C", "E", "F", "G", "H"};
        item14 = new String[]{"B", "C", "E", "F", "G", "H"};

        //初始化数据集
        dataList.add(item1);
        dataList.add(item2);
        dataList.add(item3);
        dataList.add(item4);
        dataList.add(item5);
        dataList.add(item6);
        dataList.add(item7);
        dataList.add(item8);
        dataList.add(item9);
        dataList.add(item10);
        dataList.add(item11);
        dataList.add(item12);
        dataList.add(item13);
        dataList.add(item14);

        //赋值给最小支持的数
        minSupportCount = dataList.size() * minSupport;
    }
}

实验结果
所有的频繁项目集：
在这里插入图片描述
所有的强关联规则实在太多，放不下，就展示如图所示的一部分，请各位自行测试：
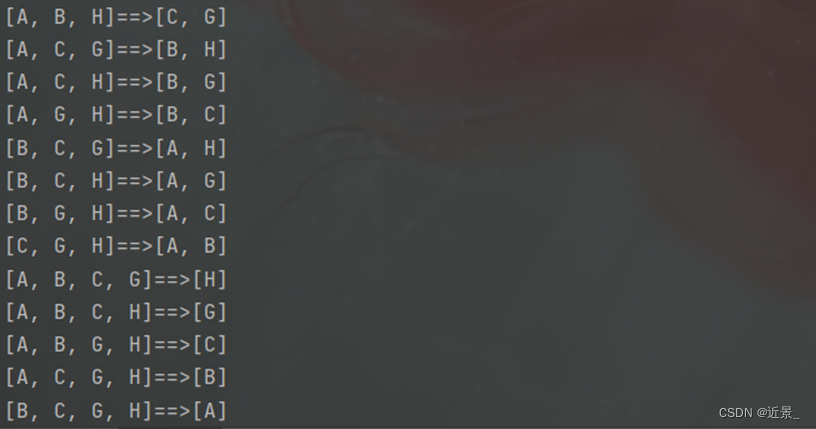
在这里插入图片描述

五、实验总结

本实验结果笔者并不保证一定是正确的，笔者仅仅是提供一种使用Java语言实现Apriori算法的思路。因为实验并没有给答案，笔者已将网络上有答案的实验数据输入程序后，程序输出的结果和答案一致，所以问题应该不大。若有写的不到位的地方，还请各位多多指点！
笔者主页还有其他数据挖掘算法的总结，欢迎各位光顾！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/99390.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

[附源码]Node.js计算机毕业设计工会会员管理系统Express

[附源码]Node.js计算机毕业设计工会会员管理系统Express

项目运行 环境配置&#xff1a; Node.js最新版 Vscode Mysql5.7 HBuilderXNavicat11Vue。 项目技术&#xff1a; Express框架 Node.js Vue 等等组成&#xff0c;B/S模式 Vscode管理前后端分离等等。 环境需要 1.运行环境&#xff1a;最好是Nodejs最新版&#xff0c;我…
阅读更多...
【Linux学习】多线程

【Linux学习】多线程

目录前言一、初识线程1. 线程的概念2. 线程的优缺点3. 线程异常4. 线程的用途二、Linux中的线程和进程1. 进程和线程的区别2. 进程中的线程共享三、Linux线程控制1. POSIX线程库2. 创建线程3. 线程终止4. 线程等待5. 线程分离四、Linux线程互斥1. 线程互斥的概念2. 互斥量mutex…
阅读更多...
蓝桥杯基础算法（一）—— 快速排序

蓝桥杯基础算法（一）—— 快速排序

文章目录1. 基本思想2. 图解过程3. 代码模板4. 例题讲解&#x1f351; 快速排序&#x1f351; 第 k 个数1. 基本思想 快速排序是 Hoare 于 1962年 提出的一种二叉树结构的交换排序方法。 其基本思想为&#xff1a; &#xff08;1&#xff09;确定分界点&#xff1a;在数组中…
阅读更多...
从零开始的MySQL(1)

从零开始的MySQL(1)

目录1.MySQL的安装2.MySQL的基本操作2.1 展示数据库2.2 创建数据库2.3 选中数据库2.4 删除数据库2.5 常用数据类型2.5.1 整形2.5.2 浮点数2.6 创建表2.7 查看表2.7 查看表结构2.8 删除表3.数据库增删改查3.1 单行插入3.2 多行插入3.3 插入日期3.4 select查询3.4.1 select3.4.2 …
阅读更多...
Jprofiler监控服务器的cpu

Jprofiler监控服务器的cpu

现象&#xff1a;压测过程中&#xff0c;发现应用服务器的cpu使用率比较高>80%&#xff0c;我们就可以判断服务器的cpu使用率太高了。 一般cpu太高有两种情况&#xff0c; 1.接口的性能非常好&#xff0c;比如响应时间<10ms&#xff0c;tps很高&#xff0c;此时的cpu使用…
阅读更多...
CSDN官方插件猿如意可以用ChatGPT啦！

CSDN官方插件猿如意可以用ChatGPT啦！

什么是 ChatGPT Chat GPT 是一种由 AI 技术驱动的自然语言处理工具&#xff0c;可让您与聊天机器人进行类似人类的对话等它是基于OpenAI的GPT-3架构进行构建的&#xff0c;并经过训练&#xff0c;以便能够回答人类的问题并进行自然对话ChatGPT可以回答关于各种话题的问题&#…
阅读更多...
基于SSM广州旅游攻略网站的设计与实现

基于SSM广州旅游攻略网站的设计与实现

开发工具(eclipse/idea/vscode等)&#xff1a; 数据库(sqlite/mysql/sqlserver等)&#xff1a; 功能模块(请用文字描述&#xff0c;至少200字)&#xff1a;
阅读更多...
【Unity】摄像机跟随鼠标移动以物体为中心旋转 物体根据视线方向移动

【Unity】摄像机跟随鼠标移动以物体为中心旋转 物体根据视线方向移动

描述 实现摄像机根据鼠标移动跟随物体旋转&#xff0c;以摄像机前物体为中心&#xff0c;摄像机围绕物体旋转&#xff0c;并使摄像机时刻指向物体 实现效果 Unity 组件设置 Camera 组件设置 Body 组件设置 实现代码 CameraRotateMove.cs 摄像机跟随和旋转 using System.Co…
阅读更多...
神经网络常用的训练方式,什么是神经网络训练法

神经网络常用的训练方式,什么是神经网络训练法

1、神经网络中的模型训练是什么意思? 无导师学习网络 神经网络中的模型训练是通过自动寻找样本中的内在规律和本质属性,自组织、自适应地改变网络参数与结构。 神经网络在系统辨识、模式识别、智能控制等领域有着广泛而吸引人的前景&#xff0c;特别在智能控制中&#xff0c;…
阅读更多...
寄存器内存读写指令（二） —— 多寄存器读写 LDM / STM

寄存器内存读写指令（二） —— 多寄存器读写 LDM / STM

有的时候&#xff0c;CPU可能会遇到 a; b; c&#xff0c;这个时候为了提升效率&#xff0c;CPU可能会一次将多个寄存器里的变量保存到内存中。这个时候之前介绍的 LDR / STR 指令虽然也能实现&#xff0c;但只能操作一个寄存器的读写。 因此&#xff0c;考虑到这点&#xff0c…
阅读更多...
基于FPGA的PWM发生器设计

基于FPGA的PWM发生器设计

目录 引言 设计说明 设计特点 设计思路 设计源码 整数除法模块
阅读更多...
超级好看的 Edge 浏览器新标签页插件：好用、好看、免费浏览器必备

超级好看的 Edge 浏览器新标签页插件：好用、好看、免费浏览器必备

BdTab 新标签页 BdTab新标签页扩展是一款免费无广告、简单好用的的高颜值新标签页扩展。 BdTab它颜值高、简单好用、支持高度自定义&#xff1a; 在登录之后支持云备份&#xff0c;支持快速切换搜索引擎&#xff0c;支持快速查看浏览历史记录和书签&#xff0c;用起来非常方便…
阅读更多...
数据结构与算法——Java实现排序算法（一）

数据结构与算法——Java实现排序算法（一）

目录 一、排序算法 1.1 排序算法基本介绍 1.2 衡量程序执行的方法 1.2.1 事后统计法 1.2.2 事前估算的方法 二、 时间复杂度 2.1 时间频度 2.2 时间复杂度 2.2.1 常见的时间复杂度 2.2.2 常数阶O(1) 2.2.3 对数阶O(log2底n) 2.2.4 线性阶O(n) 2.2.5 线性对数阶O(n…
阅读更多...
2022年PAT冬季甲级考试 25 A-3 Articulation Points

2022年PAT冬季甲级考试 25 A-3 Articulation Points

A-3 Articulation Points 分数 25 In graph theory, given a connected graph G, the vertices whose removal would disconnect G are known as articulation points. For example, vertices 1, 3, 5, and 7 are the articulation points in the graph shown by the above fi…
阅读更多...
WAYON维安功率肖特基二极管，适配器领域的助推器

WAYON维安功率肖特基二极管，适配器领域的助推器

WAYON维安功率肖特基二极管&#xff0c;适配器领域的助推器。 维安功率肖特基二极管&#xff0c;适配器领域的助推器 导言 肖特基二极管&#xff0c;是以它的发明人肖特基博士名字而命名的&#xff0c;又被称作是肖特基势垒二极管。它是金属与半导体材料相互接触&#xff0c;且…
阅读更多...
C++：类和对象：C++对象模型和 this指针

C++：类和对象：C++对象模型和 this指针

1&#xff1a;成员变量和成员函数分开存储 在C中&#xff0c;类内的成员变量和成员函数分开存储&#xff0c;只有非静态成员变量才属于类对象。 案例&#xff1a;我们写一个空类&#xff0c;然后创建一个对象&#xff0c;看看这个空对象占用多大空间。 #include<iostream…
阅读更多...
做全表扫描时数据表的内存大于 MySQL 内存，会不会被打爆？

做全表扫描时数据表的内存大于 MySQL 内存，会不会被打爆？

我查这么多数据&#xff0c;会不会把数据库内存打爆&#xff1f; 我的数据库内存只有10G&#xff0c;现在我要对一个20G的大表做全表扫描&#xff0c;会不会把数据库内存&#xff08;buffer pool&#xff09;占满然后报OOM的错误&#xff1f; 答案是不会的。 InnoDB的数据是…
阅读更多...
【图像处理 -1图像恢复】非线性过滤器修复图像

【图像处理 -1图像恢复】非线性过滤器修复图像

【论文参考】文章地址&#xff1a; https://www.researchgate.net/publication/303996052_Image_Restoration_Technique_with_Non_Linear_Filter Image Restoration 一、摘要 在本文中&#xff0c;提出了一种新的处理方法图像使用不同的过滤方法 实现Image恢复。目的是增强数…
阅读更多...
计算机网络原理第4章 网络层

计算机网络原理第4章 网络层

目录~ 4.1 网络层提供的两种服务 面向连接&#xff1a;让网络负责可靠交付&#xff0c;通信之前先建立虚电路 无连接&#xff1a;网络提供数据报服务&#xff0c;网络层提供简单灵活的、无连接的、尽最大努力交付的数据报服务 4.2 网际协议 IP 网际协议 IP 是 TCP/IP 体系…
阅读更多...
基于JAVA的校友录

基于JAVA的校友录

开发工具(eclipse/idea/vscode等)&#xff1a; 数据库(sqlite/mysql/sqlserver等)&#xff1a; 功能模块(请用文字描述&#xff0c;至少200字)&#xff1a; 网站前台&#xff1a;关于我们、联系我们、校园通知、组织信息、活动信息 管理员功能&#xff1a; 1、管理关于我们、联…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023