---

1. 基本思想

快速排序是 Hoare 于 1962年 提出的一种二叉树结构的交换排序方法。

其基本思想为：

（1）确定分界点：在数组中选出一个 key，一般是最左边的值、中间的值或是最右边的值都可以。

（2）调整区间：使得区间左边所有的数都小于等于 key，区间右边的所有的数都大于等于 key。

（3）递归处理左右两段，也就是把左右分别排序（左边的最大值一定是小于右边的最小值）

2. 图解过程

快排的思想很容易理解，难点在于如何调整区间？

首先我们选取最左边的值为 key，然后定义两个指针 i 和 j。

i 在区间的最左边，指向 left 的前一位，j 在区间的最右边指向 right 的后一位。

接着 i 先走，向中间移动，如果遇到比 key 大的值就停下来，然后 j 再向中间移动，如果遇到比 key 小的值就停下来，最后交换指针 i 和指针 j 指向的值。

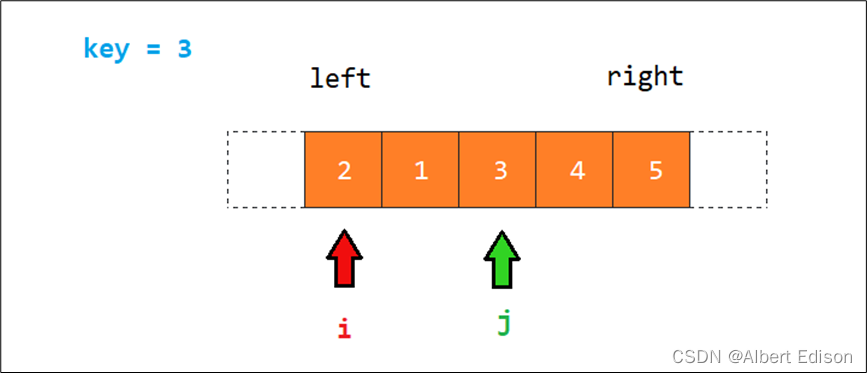
然后 i 和 j 又继续往中间走，此时 i > j，那么我们就停下来。

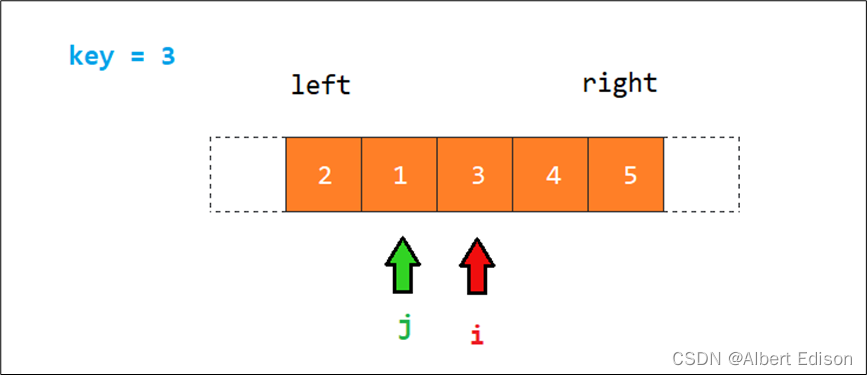
最后我们又可以重新划分区间，又重新递归左区间 left, j 和右 j + 1, right

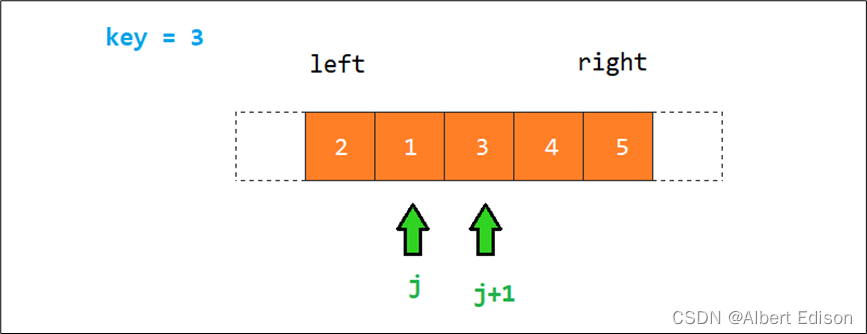
3. 代码模板

代码示例

void quick_sort(int q[], int l, int r)
{
	if (l >= r)
		return;

	int i = l - 1, j = r + 1, x = q[l + r >> 1];

	while (i < j)
	{
		// i找比x大的
		while (q[++i] < x);
		// j找比x小的
		while (q[--j] > x);
		// 走到这里，直接交换i和j下标指向的元素
		if (i < j)
			swap(q[i], q[j]);
	}

	// 递归左区间
	quick_sort(q, l, j);

	// 递归右区间
	quick_sort(q, j + 1, r);
}

i，j 是一个待排序区间的左右指针，x 是用来分界的值，这里选了中间点的值

初始化 i，j 分别为左边界的左边和右边界的右边，方便后面先递增和递减的操作

然后 >> 移位运算符，往右移 1 就表示对应数值的二进制表示往右移动 1，在数学意义上相当于数值除以 2 的下取整。

递归查找的思路很简单：

因为当 i 指针和 j 指针相遇或错过（i 跑到了 j 后面一格，一定是一格）之后，i 和 j 指针一定都无法再次满足 while 条件。

那么，此时数组的实际情况一定是 j 左边的（包括 j）小于等于哨兵元素，

i 右边的（包括 i）大于等于哨兵元素，而 i 一定是 要么等于 j，要么等于 j + 1，

因此，以 j 和 j + 1 作为分界。

4. 例题讲解

🍑 快速排序

（1）题目描述

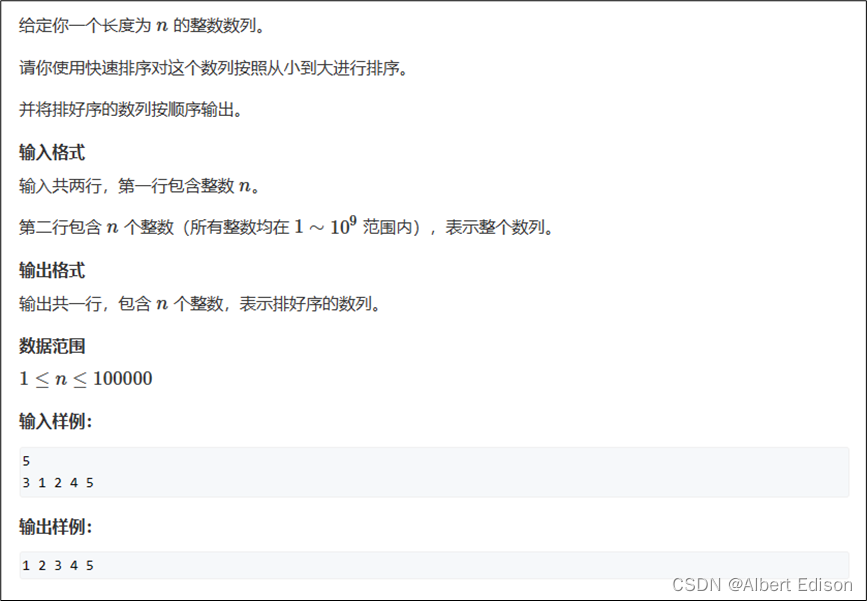
（2）代码实现

#include <iostream>
using namespace std;

const int N = 1e5+10;

int n;
int q[N];


void quick_sort(int q[], int l, int r) {
    if (l >= r) return;
    
    int i = l - 1, j = r + 1, x = q[l + r >> 1];
    
    while (i < j)
    {
        while (q[++ i] < x);
        while (q[-- j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    
    quick_sort(q, l, j);
    quick_sort(q, j+1, r);
}


int main()
{
    scanf("%d", &n);
    
    for (int i = 0; i < n; ++i) scanf("%d", &q[i]);
    
    quick_sort(q, 0, n-1);
    
    for (int i = 0; i < n; ++i) printf("%d ", q[i]);
    return 0;
}

🍑 第 k 个数

（1）题目描述

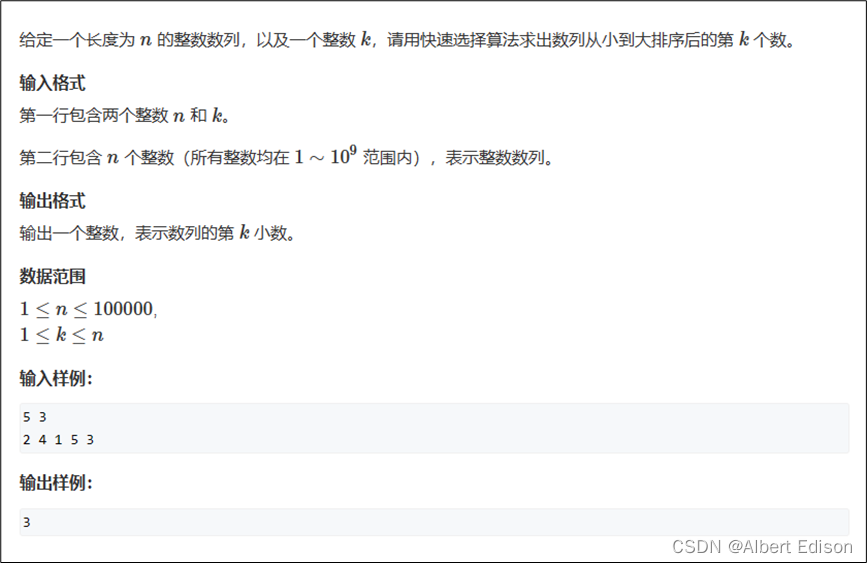
意思就是：在这个数组种，找到第 3 小的数，那么输出结果就算 3。

（2）解题思路

我们先来回顾一下快排的思路：

1）找到分界点 x（q[L]、q[(L + R) / 2]、q[R] 这三个都可以当分界点）

2）使得左边所有的数小于等于 x（left <= x），右边所有的数大于等于 x（right >= x）

3）递归排序左右区间

这道题不一样的地方在于它可以利用快排模板，但却不需要真的把所有数据排序完成，每次一分为二后，只关心自己所有的那一半，就是可以节约一半的递归时间。

当我们实现完前两步以后，现在已经把左右区间划分好了，由于左边所有的数肯定是小于等于右边所有的数，

因此左半段里面的数就是整个区间最小的数，我们统计左半段的个数，记为 SL。

同样把右半段的个数记为 SR。

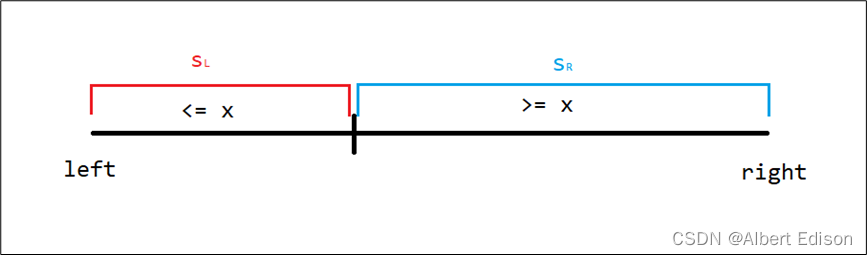
那么此时我们就可以分情况讨论：

1）如果 k <= SL，那么第 k 小的数一定在左半边，因此我们只需要递归处理左边。

2）如果 k > SR，那么第 k 小的数一定在右半边，因此我们只需要递归处理右边，那么整个区间第 k 小的数就是右半边的第 k - SL 小的数

这个其实是由快速排序演变来的，只是我们只能选择递归某一边。

位置这个参数不是一成不变的，因为如果在左侧，那么就是原来的位置，如果在右侧，那就需要减去整个左侧的长度。

这个 k 参数可以理解为 “在当前数组中的位置”，最终将确定这个位置上的值。

时间复杂度：$O(n)$

（3）代码实现

#include <iostream>
using namespace std;

const int N = 1e5+10;

int n, k;
int q[N];

int quick_sort(int l, int r, int k) {
    if (l == r) 
        return q[l];
    
    int x = q[l], i = l - 1, j = r + 1;
    
    while (i < j)
    {
        while (q[++ i] < x);
        while (q[-- j] > x);
        
        if (i < j) 
            swap(q[i], q[j]);
    }
    
    int sl = j - l + 1;
    
    if (k <= sl) //如果第K个数在左半边，就排左半边，
        return quick_sort(l, j, k); 
    
    return quick_sort(j + 1, r, k - sl); //否则就排右半边。
}

int main()
{
    cin >> n >> k;
    
    for (int i = 0; i < n; ++i) cin >> q[i];
    
    cout << quick_sort(0, n - 1, k) << endl;
    
    return 0;
}