题目：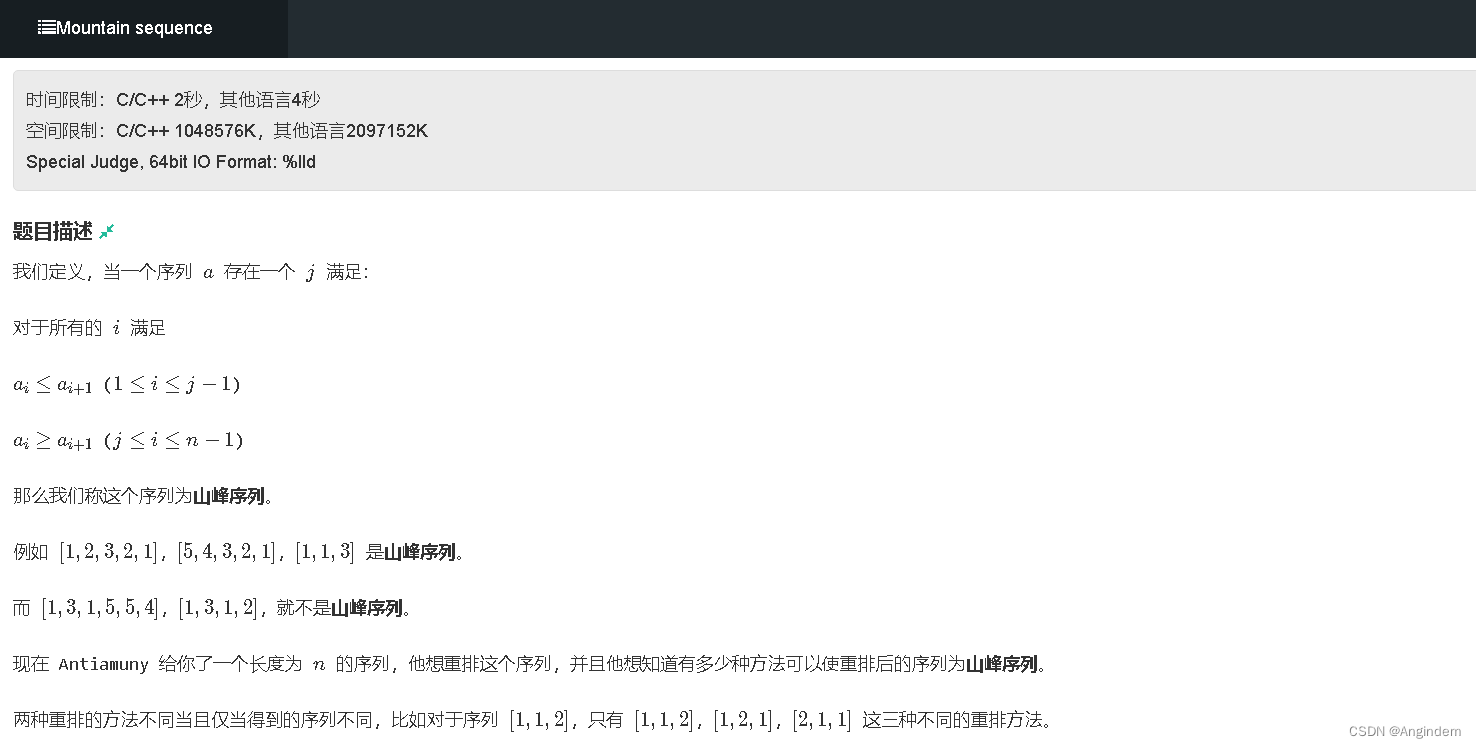

样例：

输入
`3 5 1 2 3 4 5 3 3 3 3 3 1 2 1`

输出
16 1 3

思路：

依据题意，再看数据范围，可以知道暴力肯定是不可能了，然后通过题目意思，我们可以排列模拟一下，这里排列所得结果，联系上我们数学的排列组合知识点可以知道，这个山峰序列，我们排列的时候是围绕 “山峰” 来进行排列，即围绕最大的数值来进行排列，而当出现多个最大值的时候，我们必须将多个最大值绑定在一块，通过排列得知，我们排列左边是一个结果，排列一样的右边，也是一种结果，所以有（排列个数 + 1）这里的 +1 是排列右边的结果，相当于镜面翻转。

其次，答案中至少有一种结果，即ans = 1，因为直接 sort 排序一遍，就是一个山峰序列，然后当我们记录的（排列个数 + 1）就有最终答案 ans = ans * (排列个数 + 1) % MOD 这里注意一个条件就是我们的山峰序列是围绕的，所以不用算进 ans = ans * (排列个数 + 1) % MOD

例子1：

[1 , 2 ]

ans = 1

r[1] = 1

r[2] = 1
ans = ans * (r[1] + 1) % MOD = 2

即答案只有 2 种分别是 [1 , 2 ] [2, 1 ]

代码详解如下：

#include <iostream>
#include <unordered_map>
#define endl '\n'
#define x first
#define y second
#define int long long
#define YES puts("YES")
#define NO puts("NO")
#define umap unordered_map
#pragma GCC optimize(3,"Ofast","inline")
#define ___G std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int MOD = 998244353;
int n;	// 数组大小
inline void solve()
{
	umap<int,int>r;	// 记录元素个数
	int ans = 1;	// 答案最终结果
	int maxs = -1;	// 取出  峰顶值 即 最大值
	cin >> n;
	for(int i = 0,x;i < n;++i)
	{
		cin >> x;
		++r[x];	// 统计元素个数
		maxs = max(maxs,x);		// 寻找 峰顶值
	}
	
	// 开始循环乘上每一种排列结果， 除去峰顶值的计算
	for(auto i : r) if(i.x != maxs) ans = ans * (i.y + 1) % MOD;
	
	// 输出答案
	cout << ans << endl;
}


signed main()
{
//	freopen("a.txt", "r", stdin);
	___G;
	int _t = 1;
	cin >> _t;
	while (_t--)
	{
		solve();
	}

	return 0;
}