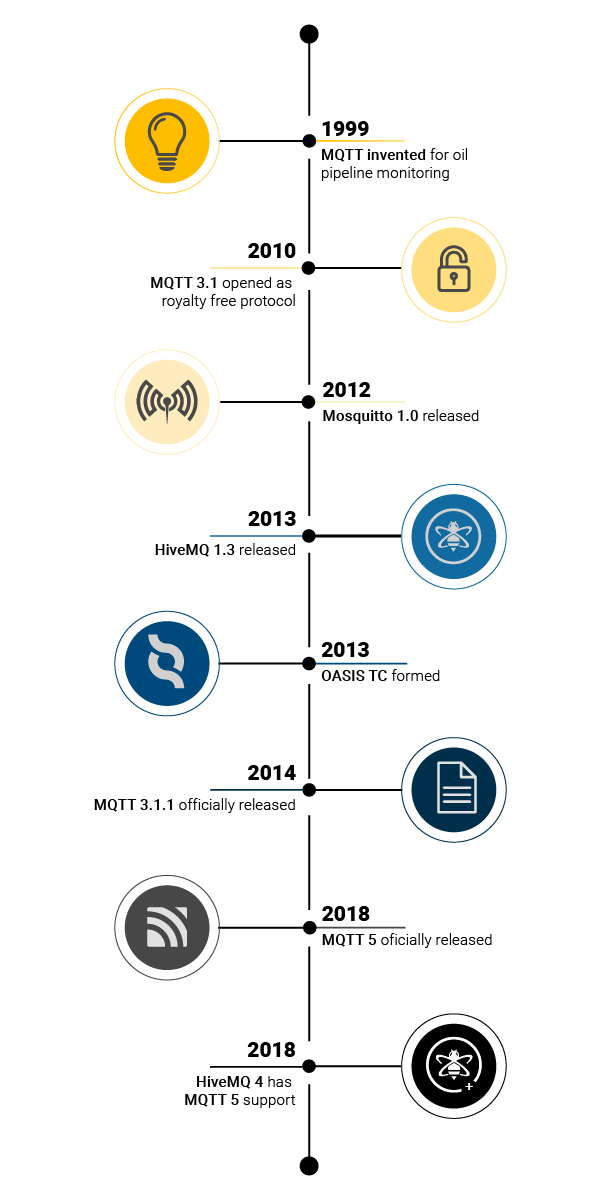
目录
- 队列
- 数组队列的“假溢出”现象
- 循环队列
- 三种判断队列空和满的方法
- 无下标(链式)
- 有下标(顺序)
- 长度标记
- go用顺序表实现一个循环队列
- 队列的链式存储结构
队列
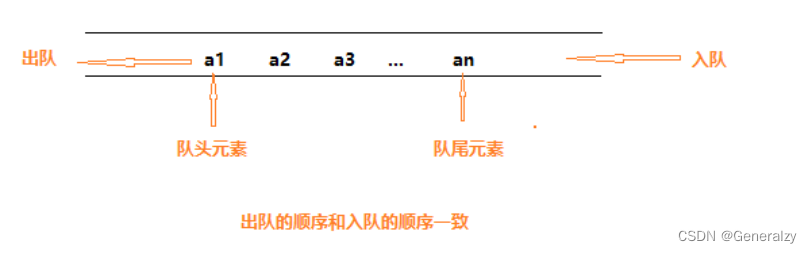
队列(queue)是只允许在一端进行插入操作,在另一端进行删除操作的线性表,简称“队”。
队列是一种先进先出(First In First Out)的线性表,简称FIFO。
允许插入的一端称为队尾(rear),允许删除的一端称为队头(front)。
向队列中插入新的数据元素称为入队,新入队的元素就成为了队列的队尾元素。
从队列中删除队头元素称为出队,其后继元素成为新的队头元素。
队列有很多种,按照存储结构划分,有链式队列,循环队列,单向队列,双端队列。实现队列的方式也有很多种,如基于链式存储结构的链接队列(又称链队列),基于顺序存储结构的队列。
数组队列的“假溢出”现象
在队列的顺序存储结构中,除了用一组地址连续的存储单元依次存放从队列头到队列尾的元素之外,还需要设置头尾两个指针front和rear,分别指示队列头元素及队尾元素的位置。
- 初始化建立空队列时,令front=rear=0
- 每当插入新的队尾元素时,“尾指针增1”
- 每当删除队头元素时,“头指针增1”
- 在非空队列中,头指针始终指向队列头元素,尾指针始终指向队列尾元素的下一个位置
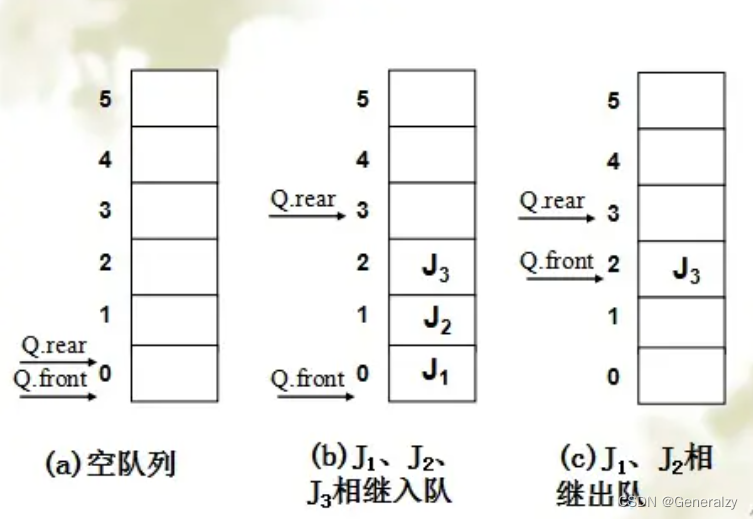
在入队和出队的操作中,头尾指针只增加不减小,致使被删除元素的空间永远无法重新利用,因此,尽管队列中实际的元素个数远远小于向量空间的规模,但也可能由于尾指针巳超出向量空间的上界而不能做入队操作,该现象称为假溢出。
解决办法:将顺序队列臆造为一个环状的空间,称之为循环队列
循环队列
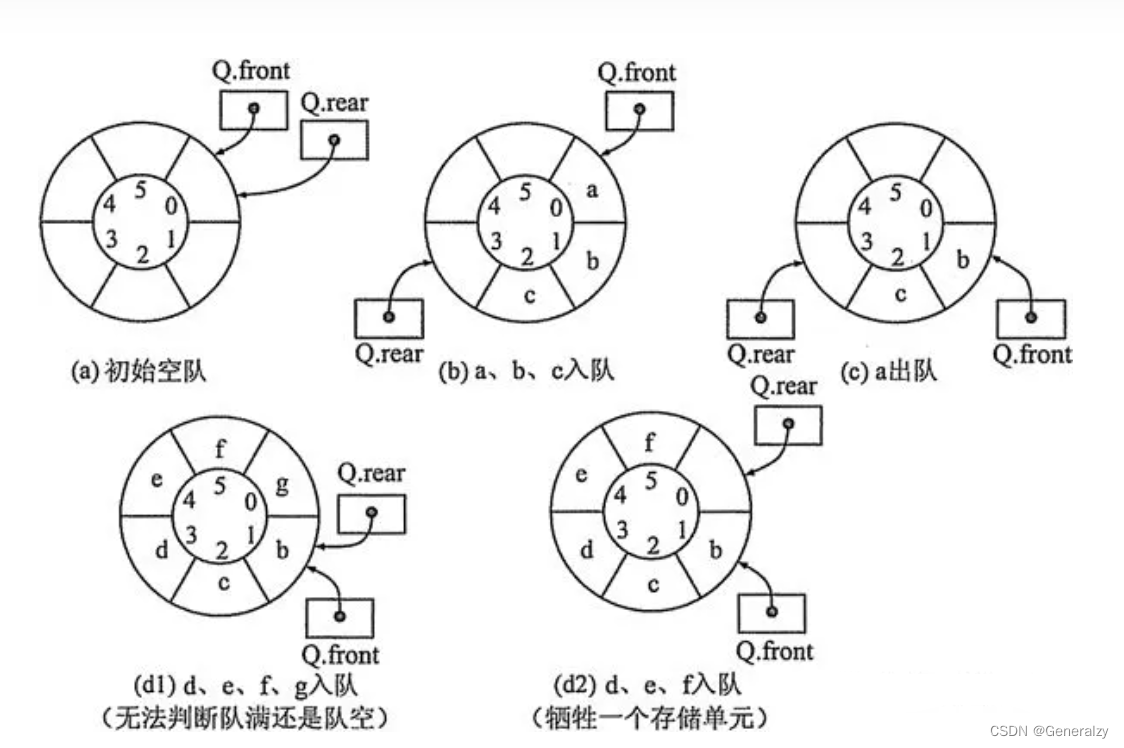
队列的头尾相接的顺序存储结构称为循环队列。
问题:当循环对列为空或满时,都是队尾指针等于队头指针,即rearfront 。当rearfront时,该是判满还是判空呢?
解决方案:
-
方案一:设置一个计数器,开始时计数器设为0,新元素入队时,计数器加1,元素出队,计数器减1。当计数器MAXSIZE时,队满;计数器0时,队空。
-
方案二:保留一个元素空间,当队尾指针指的空闲单元的后继单元是队头元素所在单元时,队满。
三种判断队列空和满的方法
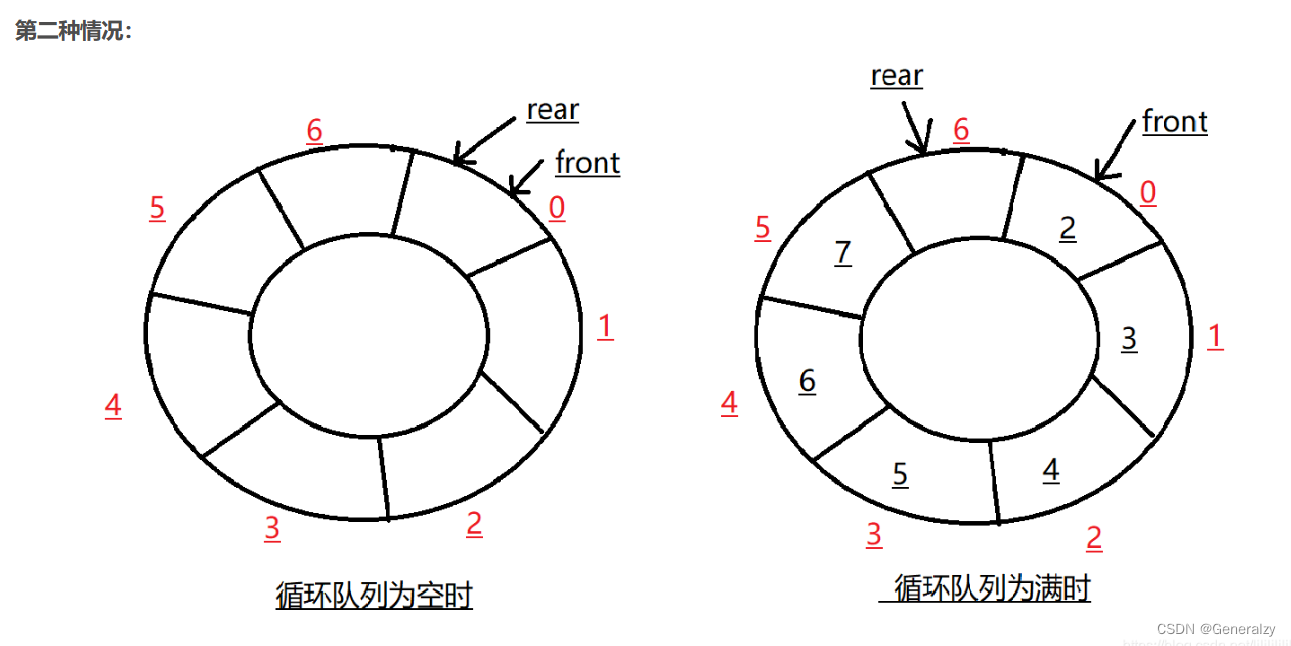
无下标(链式)
当队列为空时条件:rear == front
当队列满时条件为:rear+1 == front
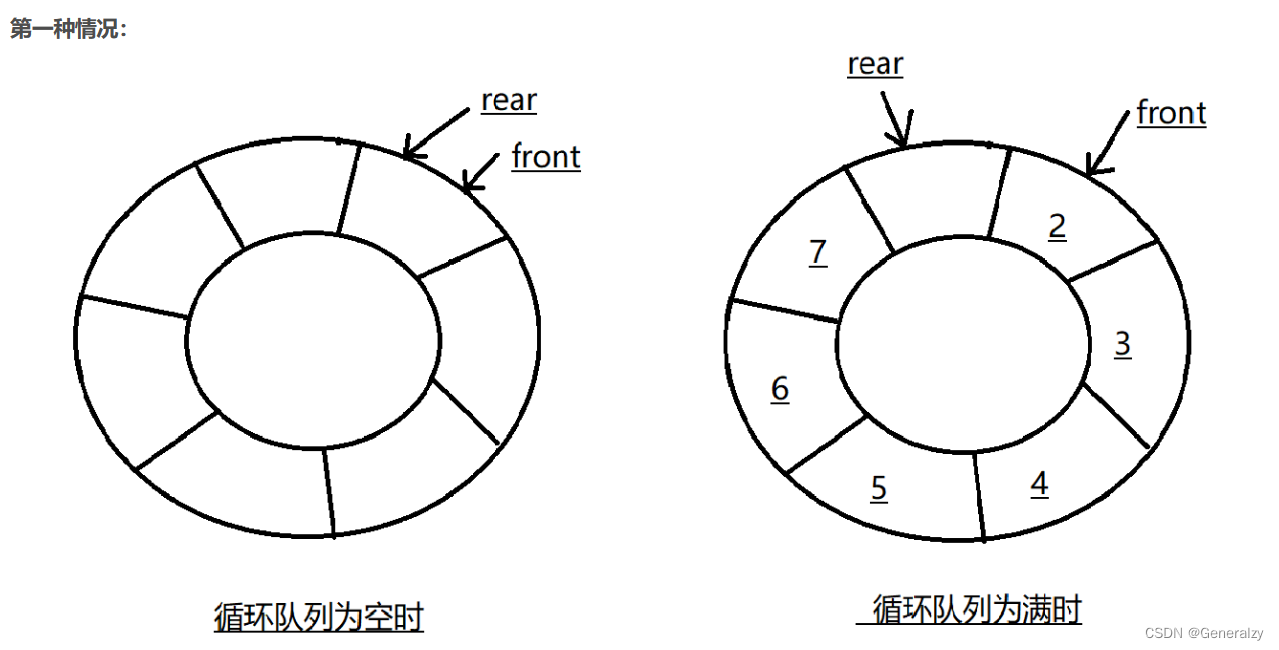
有下标(顺序)
当队列为空时条件:rear == front
当队列满时条件为:(rear+1)% maxsize == front
长度标记
设置一个标记位:
队列为空时,count == 0
当有元素入队时,count++,当count和队列的maxsize相等时,代表队列已满
go用顺序表实现一个循环队列
初始化结构体:
type LoopQueue struct {
mem []int
// length & cap
cap int
// index
front, rear int
}
func Queue(size int) *LoopQueue {
return &LoopQueue{
mem: make([]int, size),
cap: size,
front: 0,
rear: 0,
}
}
判空,判满:
func (q *LoopQueue) IsEmpty() bool {
return q.front == q.rear
}
func (q *LoopQueue) IsFull() bool {
return (q.rear+1)%q.cap == q.front
}
push,pop操作:
func (q *LoopQueue) Push(val int) error {
if q.IsFull() {
return errors.New("queue is full")
}
q.mem[q.rear] = val
// 当尾达到最大index就不能简单自增而是要循环
q.rear = (q.rear + 1) % q.cap
return nil
}
func (q *LoopQueue) Pop() (int, error) {
if q.IsEmpty() {
return -1, errors.New("empty queue")
}
pop := q.mem[q.front]
// 当头达到最大index就不能简单自增而是要循环
q.front = (q.front + 1) % q.cap
return pop, nil
}
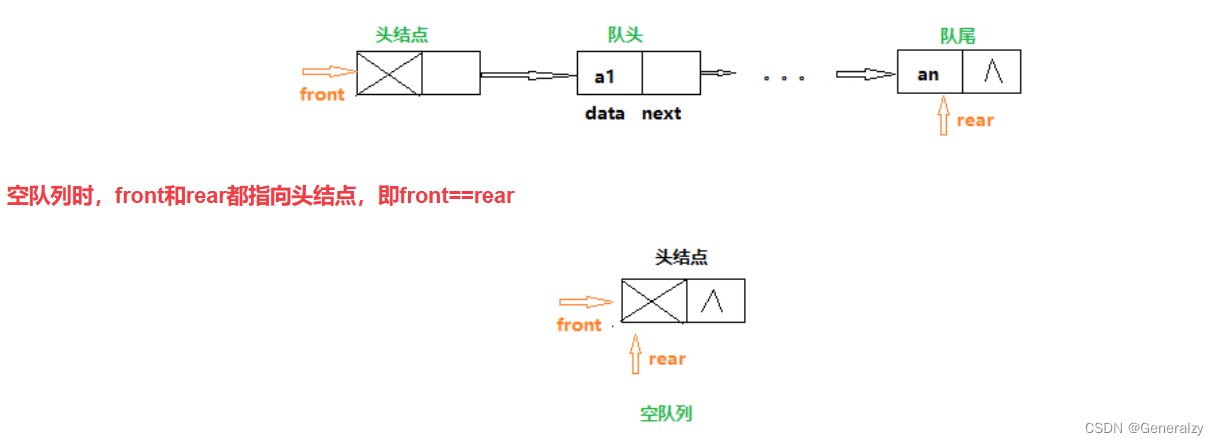
队列的链式存储结构
采用链式存储结构实现的队列称为链队列。
为了使操作更加方便,将队头指针指向链队列的头结点,而队尾指针指向终端结点。
用链表实现的队列也有“假溢出”的现象,所以go提供了Ring数据结构,只要导入"container/ring"就可以使用循环链表。
type Ring struct {
next, prev *Ring
Value any // for use by client; untouched by this library
}
func New(n int) *Ring {
if n <= 0 {
return nil
}
r := new(Ring)
p := r
for i := 1; i < n; i++ {
p.next = &Ring{prev: p}
p = p.next
}
// 头尾相连
p.next = r
r.prev = p
return r
}