梯度下降

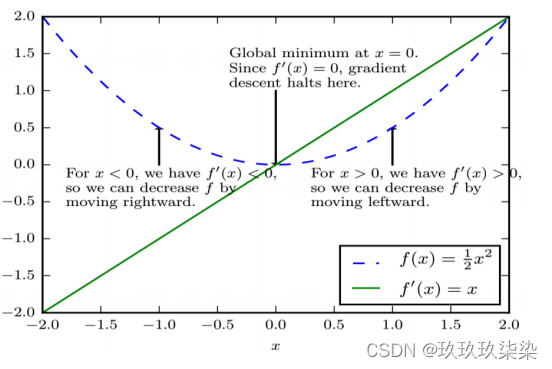
往斜率的反方向走。

临界点、驻点、拐点、鞍点、顶点（曲线）、曲率

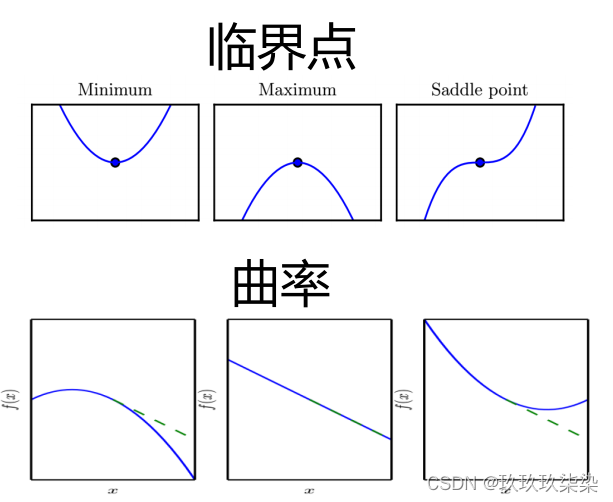
临界点：在数学中，临界点是指函数的导数为零或者不存在的点。在这些点上，函数可能存在极大值、极小值或者拐点。

驻点：驻点是指函数的导数为零的点。在这些点上，函数可能存在极大值、极小值或者拐点。

拐点：拐点是指函数的曲线在该点处由凹变凸或由凸变凹的点。在拐点处，函数的二阶导数存在且为零。

鞍点：鞍点是指函数在该点上既不是极大值也不是极小值的点。在鞍点处，函数的一阶导数为零，但二阶导数既不为零也不是正负。
现实生活中的例子或类比：想象一个山谷，其中有一座山峰。山峰的顶点就是一个局部最大值点，而山谷的底部则是一个局部最小值点。然而，在山谷的侧面，有一个点既不是山峰的顶点，也不是山谷的底部。这个点就类似于一个鞍点，因为从这个点出发，一个方向上是山谷的底部，而另一个方向上是山峰的顶点。

		总结：鞍点是一个在一阶导数为0的点上，从该点出发的一个方向是函数的极大值点，而在另一个方向是函数的极小值点。

顶点（曲线）：顶点是指曲线上的最高点或最低点。在顶点处，函数的导数为零，并且二阶导数为负（对于最高点）或正（对于最低点）。

曲率是描述曲线在某一点上弯曲程度的物理量。曲率半径是曲线上某一点处曲率的倒数。

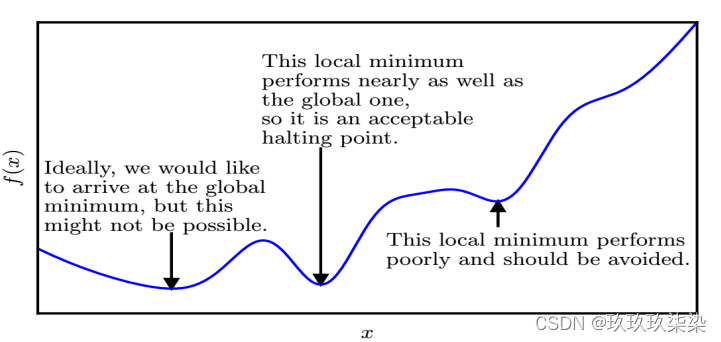
近似优化

预测最佳步长