个人主页:🍝在肯德基吃麻辣烫
我的gitee:C++仓库
个人专栏:C++专栏
文章目录
- 一、二叉搜索树的Insert操作(非递归)
- 分析过程
- 代码求解
- 二、二叉搜索树的Erase操作(非递归)
- 分析过程
- 代码求解
- 三、二叉搜索树的Find操作
- 代码求解
- 四、构造+拷贝构造+析构+赋值重载
- 节点的代码
- 构造函数
- 拷贝构造函数
- 赋值运算符重载
- 析构函数
- 二叉搜索树递归版本
- 插入操作递归版本
- 删除操作递归版本
- 总结
一、二叉搜索树的Insert操作(非递归)
分析过程
假如这里有一棵树,我们需要对这棵树插入一个新的节点:
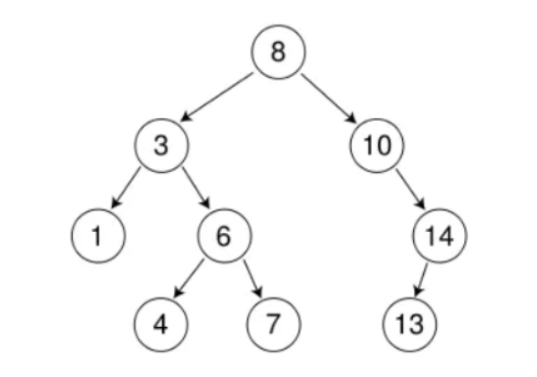
- 假如需要插入16这个节点。
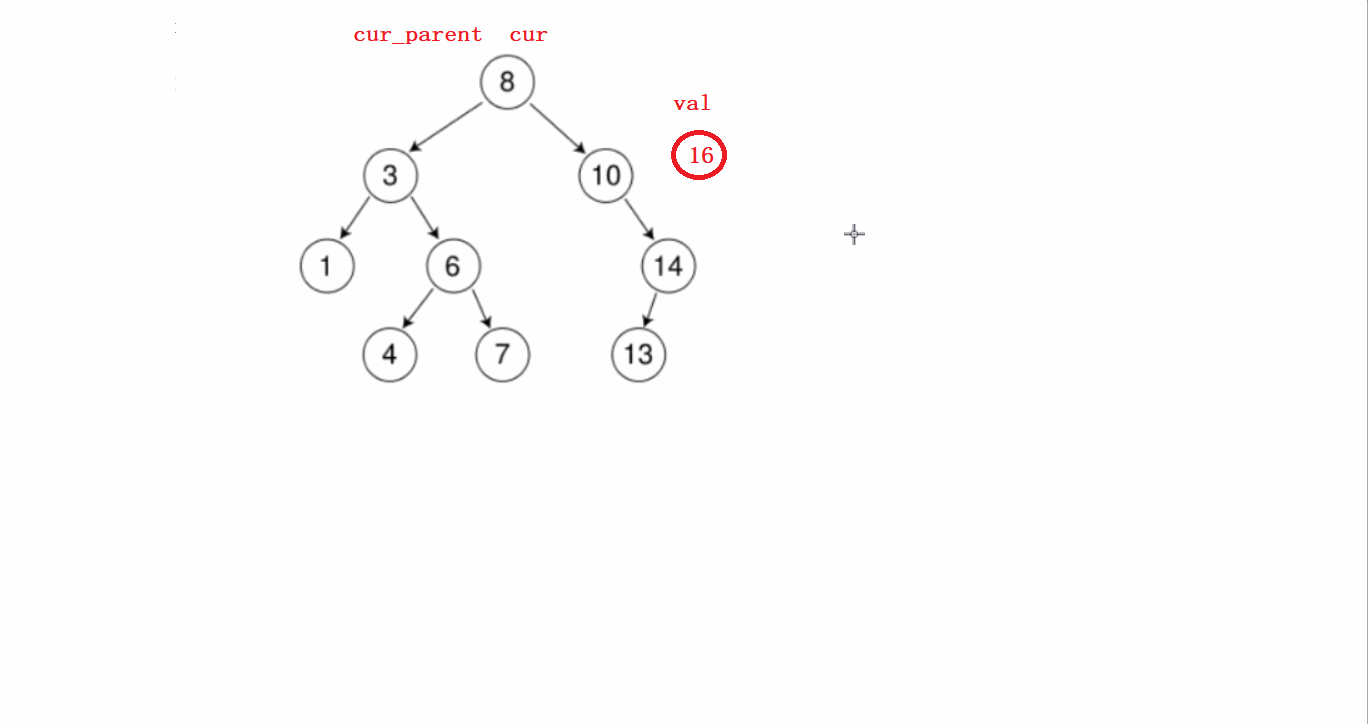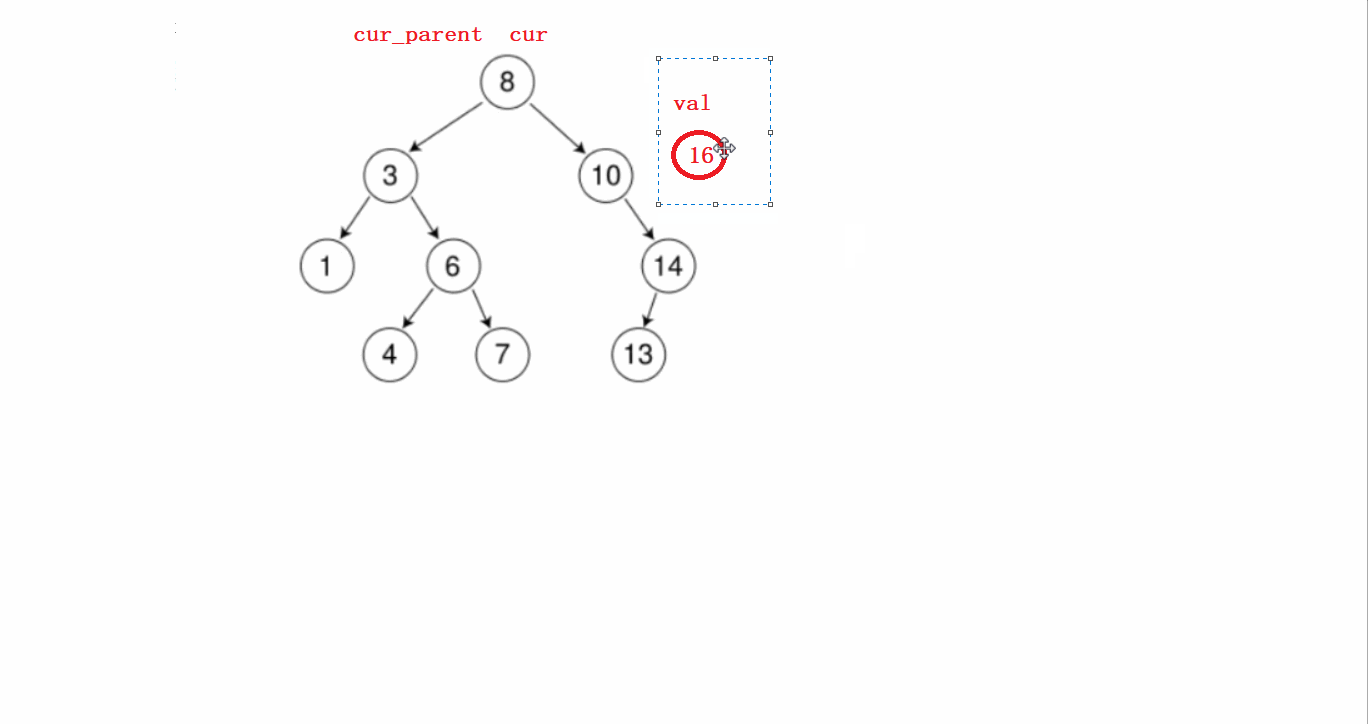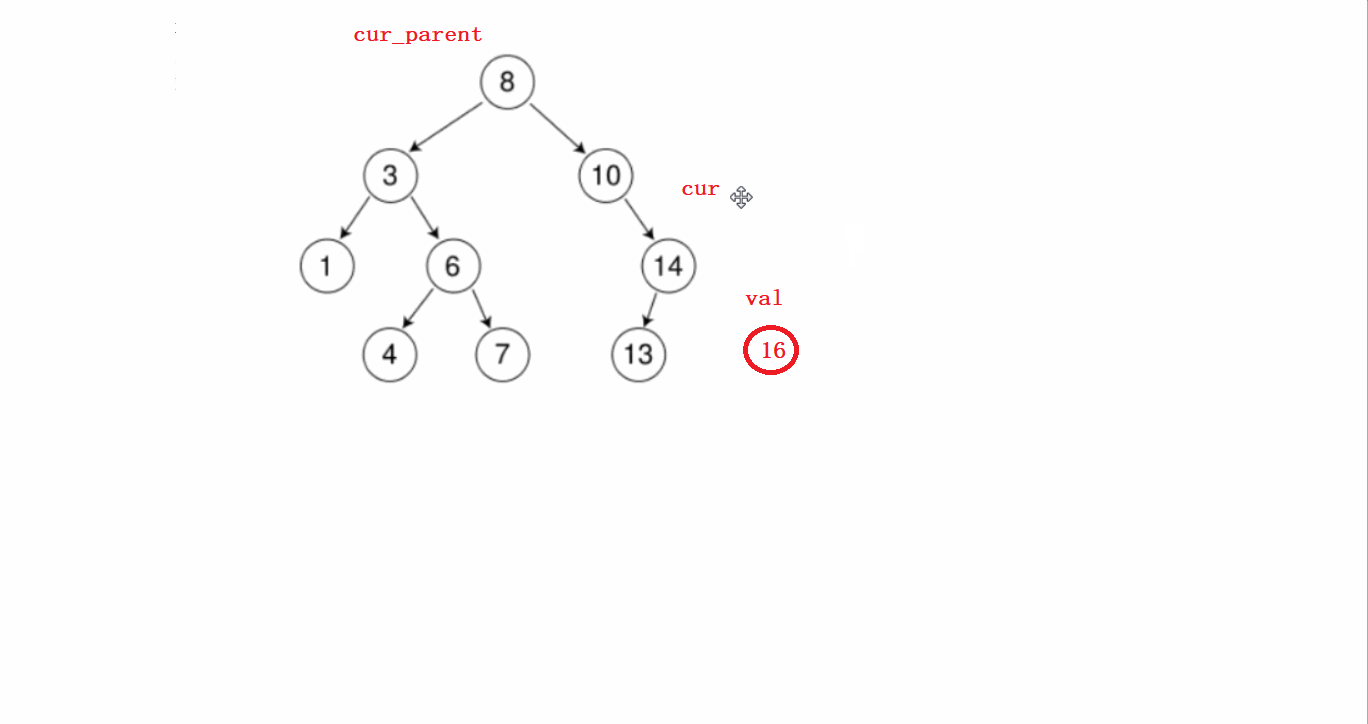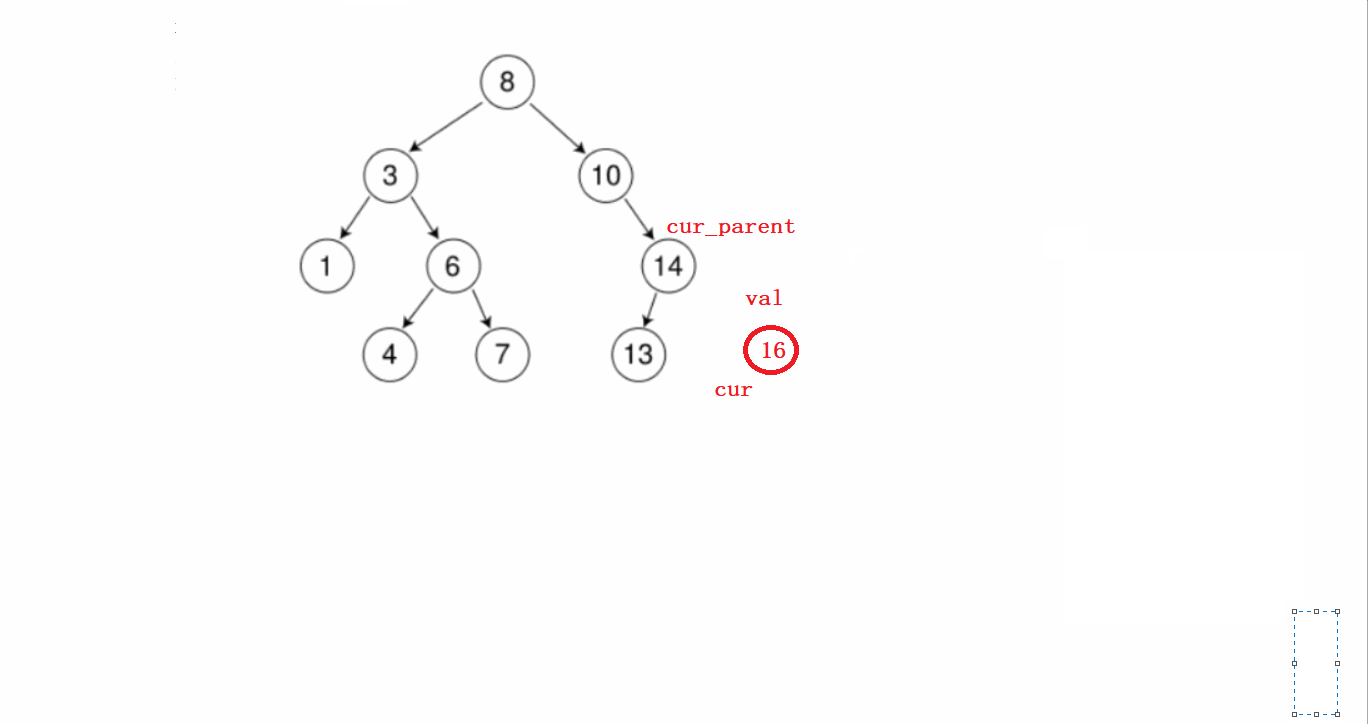
要分几个步骤进行:
1)先从根节点开始判断待插入节点和根节点谁大,根节点大就往左比较,根节点小了就往右比较。
第一步这个过程需要提前记录节点的父亲。
2)找到待插入位置后,先new一个新的节点;然后判断该节点是在前面记录的父亲节点的左边还是右边,然后连接起来即可。
代码求解
bool _Insert(Node* root, const T& val)
{
if (root == nullptr)
{
root = new Node(val);
return true;
}
Node* cur = _root;
Node* cur_par = _root;
//找插入位置
while (cur)
{
if (val > cur->_val)
{
cur_par = cur;
cur = cur->_right;
}
else if (val < cur->_val)
{
cur_par = cur;
cur = cur->_left;
}
//相同就不能插入
else
{
cout << "无法插入" << endl;
return false;
}
}
//找到插入位置了,记录父亲
Node* insNode = new Node(val);
if (cur_par->_val < val)
{
cur_par->_right = insNode;
return true;
}
else
{
cur_par->_left = insNode;
return true;
}
}
二、二叉搜索树的Erase操作(非递归)
分析过程
以下面这棵树为例:
假如我们要删除7这个节点。
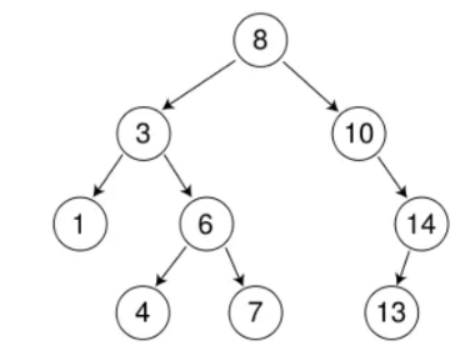
1)查找该节点是否存在于树中。
2)如果存在,先判断该节点属于下面的哪种类型:
- 1)删除的节点是叶子节点,直接删除即可。
- 2)删除的节点只有一个孩子,需要先判断它的孩子是
left还是right,然后让该节点的父亲节点指向它的孩子即可。 - 3)如果删除的节点有
left和right两个孩子,需要找一个节点进行替换;来保证这棵树在删除一个节点后还是一棵二叉搜索树。该找哪个节点来替换呢? -
- 1)找删除节点的左子树的最大节点(最右)
-
- 2)找删除节点的右子树的最小节点(最左)
找这两个节点的任意一个均可。
在这里可能有个疑问,万一找不到呢?
你放心吧!一定能找到,这是二叉搜索树的特性。
找到该节点后,将该节点与待删除的节点进行交换,然后删除交换后的节点即可。
在上面的例子中,很显然7属于叶子节点,直接删除即可。
需要注意的是:
我们在寻找那个替代节点时,像插入一样,需要记录它的父
亲,这样在删除的时候才能知道删除left孩子还是right孩子。
代码求解
bool _Erase(Node* root,const T& val)
{
//第一步:先找到要删除的节点
Node* cur = root;
Node* cur_parent = cur;
while (cur)
{
if (cur->_val > val)
{
cur_parent = cur;
cur = cur->_left;
}
else if (cur->_val < val)
{
cur_parent = cur;
cur = cur->_right;
}
//找到了
//待删除的节点分三种情况
else
{
//1.左右子树为空;2.其中一个子树为空
if (cur->_left == nullptr)
{
//要知道我是父亲的左还是右
if (cur_parent->_left == cur)
{
cur_parent->_left = cur->_right;
}
else if (cur_parent->_right == cur)
{
cur_parent->_right = cur->_right;
}
}
else if (cur->_right == nullptr)
{
//要知道我是父亲的左还是右
if (cur_parent->_left == cur)
{
cur_parent->_left = cur->_left;
}
else if (cur_parent->_right == cur)
{
cur_parent->_right = cur->_left;
}
}
//3.删除的节点左右都不为空
else
{
//先找替代节点
//找左子树的最大节点或者右子树的最小节点来替代
// 最右 最左
Node* lParent = cur;
Node* leftMax = cur->_left;
while (leftMax->_right)
{
lParent = leftMax;
leftMax = leftMax->_right;
}
//找到了,进行替换
swap(cur->_val, leftMax->_val);
//替换完成后,必须删除该节点,不能用递归删除。
//因为如果用递归,可能就找不到要删除的节点了
//这里还要判断leftMax这个替换节点是它父亲的左还是右子节点
//因为有一种极端情况是,leftMax是在父亲的左边
if (lParent->_right == leftMax)
{
lParent->_right = leftMax->_left;
//leftMax是左子树的最右节点了,它不会有右孩子,但可能有左孩子
}
else if (lParent->_left == leftMax)
{
lParent->_left = leftMax->_left;
}
cur = leftMax;
}
delete cur;
cur = nullptr;
return true;
}
}
return false;
}
三、二叉搜索树的Find操作
查找节点过于简单,直接贴代码。
代码求解
bool _Find(Node* root, const T& val)
{
if (root == nullptr)
{
return false;
}
Node* cur = _root;
while (cur)
{
if (cur->_val < val)
{
cur = cur->_right;
}
else if (cur->_val > val)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
四、构造+拷贝构造+析构+赋值重载
节点的代码
template<class T>
struct BSTreeNode
{
BSTreeNode(const T& val)
:_left(nullptr)
, _right(nullptr)
, _val(val)
{}
BSTreeNode<T>* _left;
BSTreeNode<T>* _right;
T _val;
};
构造函数
BSTree()
:_root(nullptr)
{}
拷贝构造函数
拷贝构造就是将一棵已有的树对每一个节点进行拷贝即可。
这个过程是深拷贝。
由于我们需要将每一个节点都进行拷贝并连接起来。所以这里需要前序遍历的思想处理。
Node* Copy(Node* root)
{
if (root == nullptr)
{
return nullptr;
}
Node* Copyroot = new Node(root->_val);
Copyroot->_left = Copy(root->_left);
Copyroot->_right = Copy(root->_right);
return Copyroot;
}
赋值运算符重载
这里的赋值重载可以用现代写法:
1)先将原树传给operator=()函数,用生成临时对象的方式传递,然后让被赋值的树的_root与该临时对象树的_root进行交换即可。
BSTree<T>& operator=(BSTree<T> t)
{
swap(_root, t._root);
return *this;
}
这样写的好处是:
1)t是一个临时对象,出了作用域会自己调用析构函数进行销毁。
2)_root和t._root交换后,原来这棵树会被临时对象销毁。
析构函数
将一棵树的每一个节点进行释放,就需要从下往上进行逐一释放,这个就用到后续遍历的思想。
~BSTree()
{
Destroy(_root);
}
//后续遍历销毁
void Destroy(Node* root)
{
if (root == nullptr)
{
return;
}
Destroy(root->_left);
Destroy(root->_right);
delete root;
root = nullptr;
}
二叉搜索树递归版本
插入操作递归版本
原理与非递归版本是一样的。
最大的区别是,在root的前面加上了一个引用。
- 1)先找到待插入位置
- 2)进行插入即可。
这里不再需要记录父亲的原因是:
加了引用后,当遇到空节点时,让
root = new Node(val);
这个操作即可,因为当前的root是上一层栈帧的root节点的孩子(不用管是左孩子还是右孩子)
执行完成这个代码后,相当于让上一层栈帧中的root的孩子
指向了一个New出来的节点。这样就完成了插入。
bool _InsertR(Node*& root, const T& val)
{
if (root == nullptr)
{
root = new Node(val);
return true;
}
if (root->_val < val)
{
_InsertR(root->_right, val);
}
else if (root->_val > val)
{
_InsertR(root->_left, val);
}
//相同不能插入
return false;
}
删除操作递归版本
删除的过程与非递归版本是一样的。
1)先找到删除的节点。
找到该节点后,该节点同样有三种情况:
- 1)该节点是叶子节点
- 2)该节点只有一个孩子
- 3)该节点有两个孩子(需要找替代节点)
前面两种情况的处理方法是一样的。
2)判断该节点是属于上面三种的哪一种,如果是前面两种,只需要判断该节点的left为空还是right为空即可。
就相应地执行:
root = root->_right;
或者
root = root->_left;
这两个操作即可。
以为当前栈桢的root是上一层栈桢中root的孩子(不用管是做孩子还是右孩子)
这个代码的意思就是:
让上一层栈桢的root的left/right指向当前层栈桢的root的left/right

bool _EraseR(Node*& root, const T& val)
{
if (root == nullptr)
{
return false;
}
if (root->_val < val)
{
return _EraseR(root->_right, val);
}
else if (root->_val > val)
{
return _EraseR(root->_left, val);
}
//找到了
else
{
Node* del = root;
//同样有三种情况
//这是因为root是上一个root的left/right的别名
if (root->_left == nullptr)
{
root = root->_right;
}
else if (root->_right == nullptr)
{
root = root->_left;
}
else
{
//找到替代的节点
Node* leftMax = root->_left;
while (leftMax->_right)
{
leftMax = leftMax->_right;
}
//找到之后,交换
swap(leftMax->_val, root->_val);
return _EraseR(root->_left, val);
//不能这样
//return _Erase(leftMax, val);
//这样不能保证连接关系正确
}
delete del;
return true;
}
}
总结
本文章讲述了二叉搜索树的增删查改功能,其中有一些细节需要特别注意。