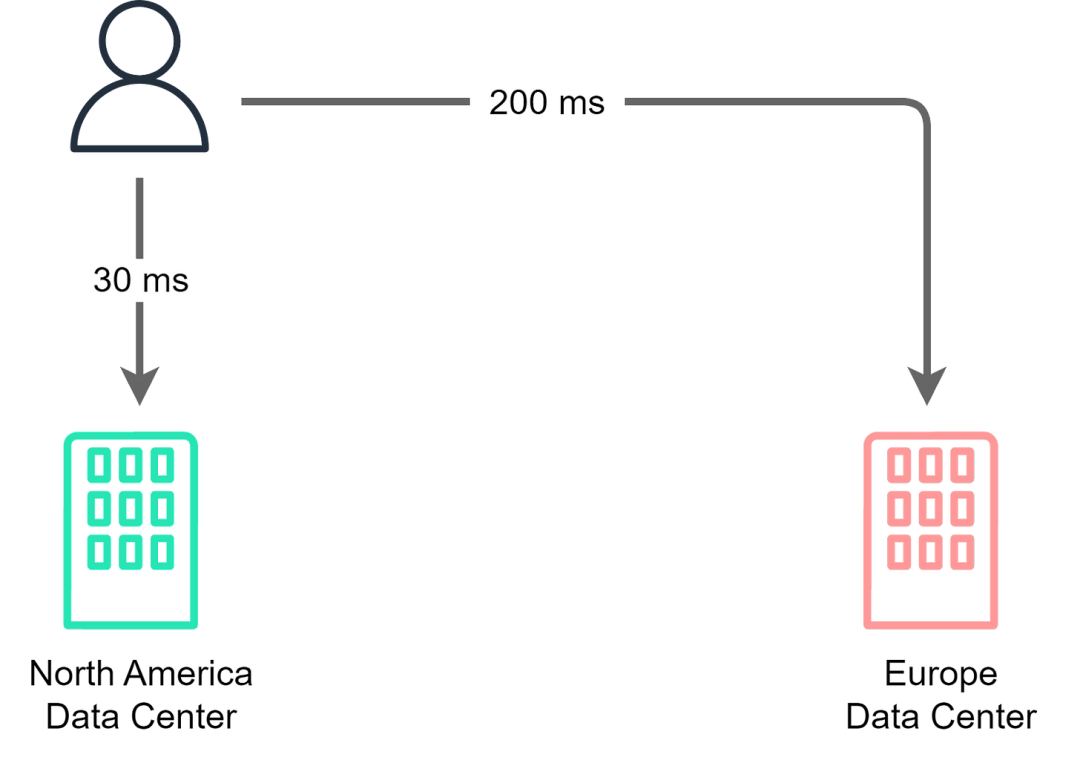
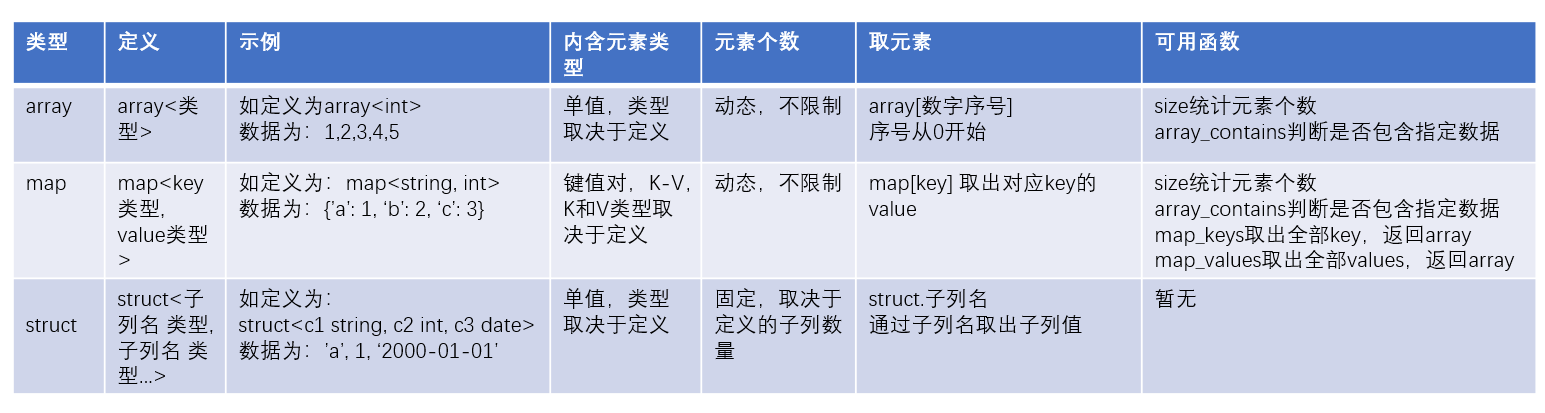
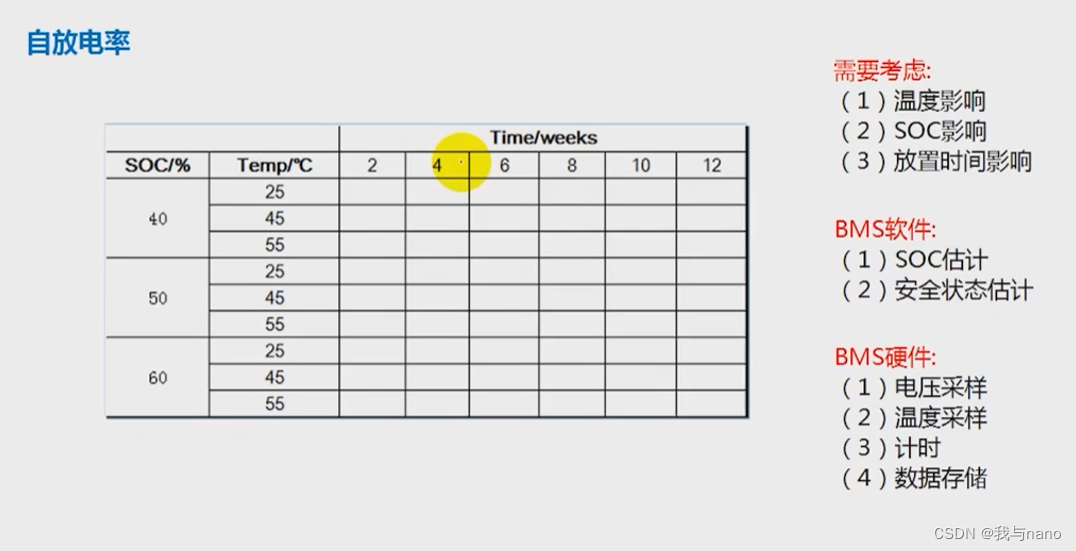
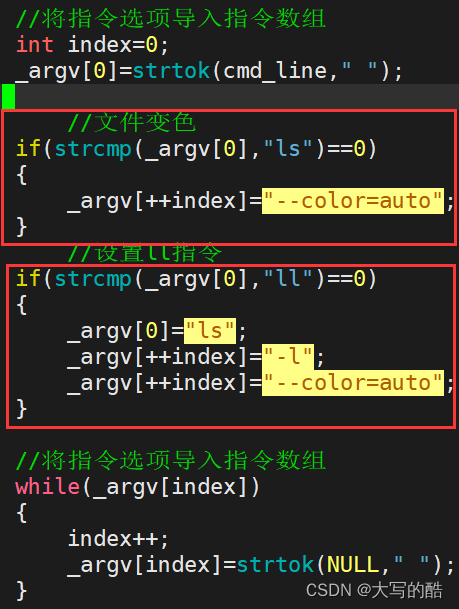
1. 跳跃游戏

题目

        LeetCode55 给定一个非负整数数组，最初位于数组的第一个位置，数组中的每个元素代表你再该位置可以跳跃的最大长度，判断你是否能够达到最后一个位置。

思路

        如果当前位置元素如果是3，我们无需考虑是跳几步，关键是判断能否达到终点，以及当前步数所能覆盖的最远距离，每次遍历更新覆盖的最远位置，只要满足 i 小于覆盖的最远距离，就满足要求，一直遍历，如果循环结束没有遍历完，就返回false。

针对上图：

1. 在第二张图中，第一个元素，nums[0] = 2,此时conver = 2能覆盖到{3，1}两个元素，就可以边遍历边更新conver的最大值。
2. 继续遍历，第二个元素nums[1] = 3,此时覆盖范围更新cover=4.{1,1,4}三个位置。
3. 继续遍历nums[2] = 1,cover=2,Math.max(4,2) = 4,此时conver > nums.length - 1。

代码

    public boolean canJump(int[] nums){
        if (nums.length == 1){
            return true;
        }
        //初始覆盖范围是0
        int conver = 0;
        //在覆盖范围内更新最大的覆盖范围
        for (int i = 0; i <= conver; i++) {
            conver = Math.max(conver, i + nums[i]);
            if (conver >= nums.length - 1){
                return true;
            }
        }
        return false;
    }

2. 最短跳跃游戏

题目

        在上题的基础上，假设一定能到达表尾，求最少要达到的步数，LeetCode45有三种走法，

{2,3,4},{2,1,1,4},{2,3,1,1,4}。

思路

需要用到四个指针：

• left用来一步步遍历数组
• steps用来记录到达当前位置的最少步数，
• right表示当前步数下能够覆盖到的最大范围。
• 我们还需要一个临时变量conver，加入left到达right时才能更新right

        在这个图中，开始的元素是2，如果只走一步，step=1，可跳的范围是{3,1}。也就是如果只走一步，最远只能到达1，此时conver=nums[0] = 2,因此我们用right=nums[2]来保存这个位置，这表示的就是走一步最远只能到nums[2]。

        每次更新最大覆盖范围，当left指针和right指针重合的时候代表，这步走完，也就是left=1的时候，第一步走完，更新step=2，根据覆盖范围大小重新定位right。

第二步，right表示当前步数最大能到的位置，第二步最大到的位置是3，继续边遍历边更新最大覆盖，当left=right的时候上一步走完，更新right位置

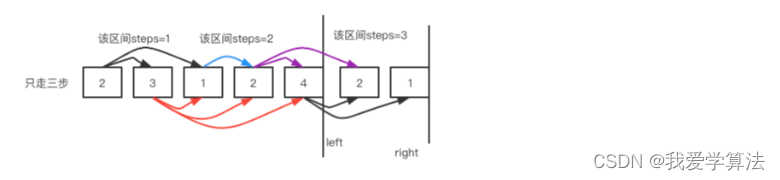
right指针>=数组长度的时候，代表走完，

简单总结来说就是，遍历记录，每次覆盖范围最大到的位置，当left和right重合的时候更新步数，保证每次都是走的最大步数

代码

    public int jump(int[] nums){
        int right = 0;
        int maxPosition = 0;
        int steps = 0;
        for (int left = 0; left < nums.length; left++) {
            //找最远的跳
            maxPosition = Math.max(maxPosition,nums[left] + left);
            if (left == right){//最大步数走完，更新下次步数
                right = maxPosition;
                steps++;
            }
            //到达尾部
            if (right >= nums.length - 1){
                return steps;
            }
        }
        return steps;
    }