题目解析

首先我们来分析一下本题的思路

题目说到要我们在一个整数数组中去寻找三元组，而且呢这三个数字所相加的和为0，而且呢这三个数的位置还要不一样
我们以这个示例1为例来看看，我列出了3种可能性，分别是[-1, 0, 1]、[-1, 2, -1]、[0, 1, -1]，不过呢我们仔细看这个题意中的概念，又可以知道这些三元组还不可以重复，那么第一个和第三个我们就需要考虑到去重

💬 但是要如何去求解本题呢，怎么去找出这些三元组呢？找出之后又该如何去做一个去重的操作呢？我们马上进行算法原理分析

算法原理分析

接下去我将通过分析算法原理来讲解本题该如何去进行求解

排序 + 暴力枚举 + set去重

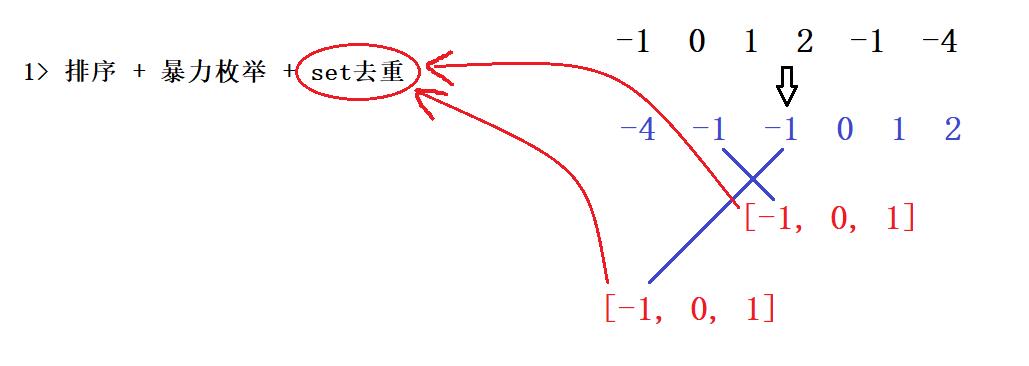
首先第一种，我们能想到的一定是暴力枚举

不过在这之前呢，我们首先要对这些整型数据去做一个排序的操作，在排完序之后我们通过暴力枚举的方式在找出两个三元组，可以看出这两个三元组的是重复的，所以我们要去做一个去重的操作
对于这步操作的话如果读者有学习过C++中的unordered_set和Java中的Hashset的话就可以知道如果我们将重复的数据扔到集合中的话就会去做一个自动去重的操作

💬 对于上面这种解法的代码就不给出了，读者可以自己去写写看

排序 + 单调性 + 双指针划分思想

我们主要的话是来讲这种解法

对于比较优的解法，我们首先应该要考虑到的就是【双指针】，如果有做过和为s的两个数字，那么就可以知道使用双指针来进行求解的话会事半而功倍
之前我们是利用双指针去求解两个的和，那现在要求解三个数的和呢？其实也是一样的，我们看到下面的这张图，首先的话我们将第一个数去做一个固定，然后呢让left指针指向i + 1的位置，right指针指向nums.size() - 1的位置，然后通过这两个指针的遍历去寻找不同的三元组即可

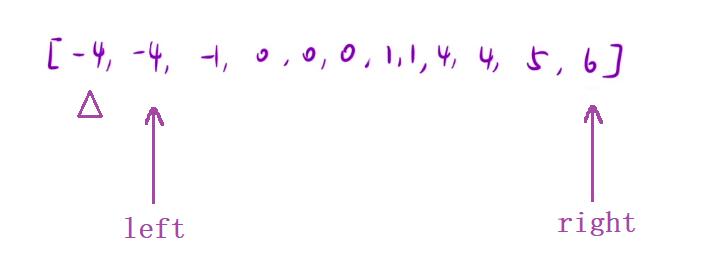
💬 那有同学说，这在遍历的过程中要怎么去进行判断呢？

其实的话这很简单，因为我们首先固定了一个数a，因为【三数之和需要为0】，那么接下去在遍历后面的这两个数的时只需要判断它们相加之和为-a即可，也就是这个数a的相反数

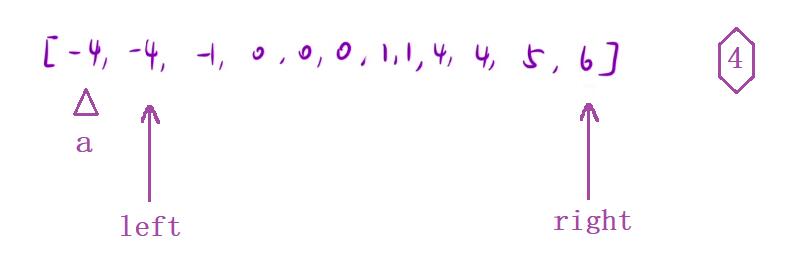
所以我们来梳理一下这个逻辑

再来模拟一下这个过程，具体的双指针判断逻辑就不解释了，读者可以去看看上面的那道题，然后再通过看下面的代码来理解这个匹配的过程

最后呢我们可以看到这三个数被找到了，那此时就可以将其放入结果集中去

所以接下去呢我们还需要去处理一些【细节】方面的问题

首先第一个的话就是让这个left和right指针还需要继续去做移动的操作，因为我们是要找到这组数据中所有的三元组

left++;right--;

第二个的话就是我们在上面所说到过的话需要考虑到的去重问题，那要怎么去重呢？

其实的话这很简单，当在执行完left++之后我们需要去判断当前所指的数字和上一个数字是否相同，如果出现了相同情况的话，就让left++，跳过这个数。对于上面的这段逻辑我们需要放在【while】循环中执行，因为可能出现很多连续相同的数据

while(nums[left - 1] == nums[left]) left++;

那对于右侧的这个数也是一样，不过是当前的这个数和后一个数去进行比较

while(nums[right] == nums[right + 1]) right--;

除了这两块的去重逻辑，其实还有一个地方也需要考虑到去重的问题，那就是外部读这个数a，读者可以思考一下，第一次我们已经对这个【-4】做了一轮的判断，那此时如果再去做一轮的判断的话就是多次一举了

所以呢我们还需要对这个i做去重的逻辑，和left是一致的

// i的去重【防止越界】
i++;
while(nums[i] == nums[i - 1])  i++;

你认为这么就完了吗，那也太小瞧这道题了，毕竟也是力扣中的困难题

我们来看一下下面的这种情况，所有的数字都是0，那么在第一次遍历的时候就天然满足了，于是就进入继续查找的逻辑，但是呢因为i、l、r所指的数据都是一样的，所以在进行【while】循环的时候会一直地进行移动，此时就会造成l超过r或者r超过l的情况，不仅如此，i在遍历的时候会碰到类似的情况

所以我们应该把去重的逻辑做一个修改，可以起到防止越界的效果✔

left++;right--;
// left与right的去重【防止越界】
while(left < right && nums[left - 1] == nums[left]) left++;
while(left < right && nums[right] == nums[right + 1]) right--;

// i的去重【防止越界】
i++;
while(i < n && nums[i] == nums[i - 1])  i++;

💬 以上就是【双指针】算法原理的分析，读者可以在阅读完之后试着自己写写看代码，很多细节的处理对代码能力的提升很有帮助

复杂度

时间复杂度:

因为我们在遍历的时候, 每次去固定一个数a，然后下标为i，接着从[i + 1, n - 1]的地方进行遍历，复杂度为： $O(n^2)$

空间复杂度:

因为没有去堆区申请任何空间，所以空间复杂度为 $O (1)$

Code

以下是整体的代码展示

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        // 1.排序
        sort(nums.begin(), nums.end());

        // 2.利用双指针解决问题
        vector<vector<int>> result;
        int n = nums.size();
        int i = 0;
        while(i < n)    // 固定a
        {
            // 若发现a > 0的话，则后面的nums[left] + nums[right]不会 < 0
            if(nums[i] > 0) break;  
            int left = i + 1, right = nums.size() - 1, target = -nums[i];
            while(left < right)
            {
                int sum = nums[left] + nums[right];
                if(sum < target){
                    left++;
                }else if(sum > target){
                    right--;
                }else{
                    // 找到了，放入结果集
                    result.push_back({nums[i], nums[left], nums[right]});
                    left++;right--;
                    
                    // left与right的去重【防止越界】
                    while(left < right && nums[left - 1] == nums[left]) left++;
                    while(left < right && nums[right] == nums[right + 1]) right--;
                }
            }
            // i的去重【防止越界】
            i++;
            while(i < n && nums[i] == nums[i - 1])  i++;
        }
        return result;
    }
};