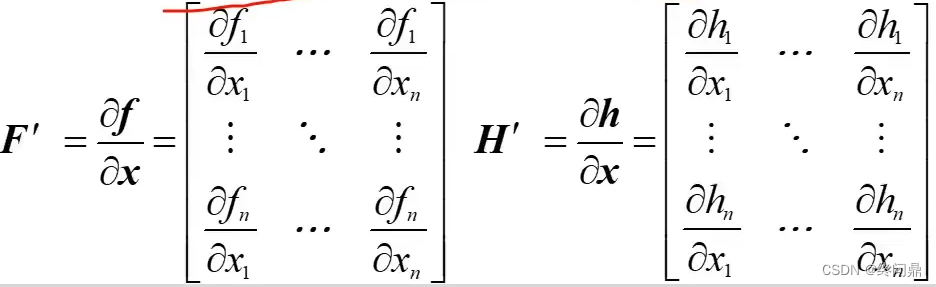对极几何与三角化求3D空间坐标

news2024/9/26 5:17:16

一，使用对极几何约束求R,T

第一步：特征匹配。提取出有效的匹配点

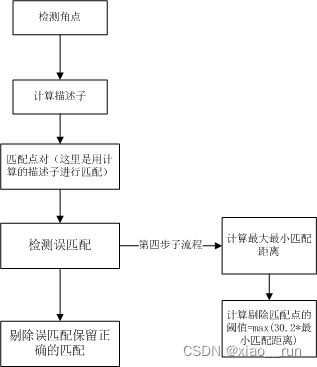
void find_feature_matches(const Mat &img_1, const Mat &img_2,
                          std::vector<KeyPoint> &keypoints_1,
                          std::vector<KeyPoint> &keypoints_2,
                          std::vector<DMatch> &matches) {
  //-- 初始化
  Mat descriptors_1, descriptors_2;
  // used in OpenCV3
  Ptr<FeatureDetector> detector = ORB::create();
  Ptr<DescriptorExtractor> descriptor = ORB::create();
  // use this if you are in OpenCV2
  // Ptr<FeatureDetector> detector = FeatureDetector::create ( "ORB" );
  // Ptr<DescriptorExtractor> descriptor = DescriptorExtractor::create ( "ORB" );
  Ptr<DescriptorMatcher> matcher = DescriptorMatcher::create("BruteForce-Hamming");
  //-- 第一步:检测 Oriented FAST 角点位置
  detector->detect(img_1, keypoints_1);
  detector->detect(img_2, keypoints_2);
 
  //-- 第二步:根据角点位置计算 BRIEF 描述子
  descriptor->compute(img_1, keypoints_1, descriptors_1);
  descriptor->compute(img_2, keypoints_2, descriptors_2);
 
  //-- 第三步:对两幅图像中的BRIEF描述子进行匹配，使用 Hamming 距离
  vector<DMatch> match;
  // BFMatcher matcher ( NORM_HAMMING );
  matcher->match(descriptors_1, descriptors_2, match);
 
  //-- 第四步:匹配点对筛选
  double min_dist = 10000, max_dist = 0;
 
  //找出所有匹配之间的最小距离和最大距离, 即是最相似的和最不相似的两组点之间的距离
  for (int i = 0; i < descriptors_1.rows; i++) {
    double dist = match[i].distance;
    if (dist < min_dist) min_dist = dist;
    if (dist > max_dist) max_dist = dist;
  }
 
  printf("-- Max dist : %f \n", max_dist);
  printf("-- Min dist : %f \n", min_dist);
 
  //当描述子之间的距离大于两倍的最小距离时,即认为匹配有误.但有时候最小距离会非常小,设置一个经验值30作为下限.
  for (int i = 0; i < descriptors_1.rows; i++) {
    if (match[i].distance <= max(2 * min_dist, 30.0)) {
      matches.push_back(match[i]);
    }
  }
}

二、使用本质矩阵求解R，T

第二步：根据匹配点对，依据对极几何约束原理，求相机运动的R,t

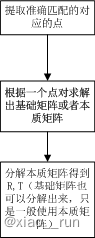
void pose_estimation_2d2d(
  const std::vector<KeyPoint> &keypoints_1,
  const std::vector<KeyPoint> &keypoints_2,
  const std::vector<DMatch> &matches,
  Mat &R, Mat &t) {
  // 相机内参,TUM Freiburg2
  Mat K = (Mat_<double>(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1);
 
  //-- 把匹配点转换为vector<Point2f>的形式
  vector<Point2f> points1;
  vector<Point2f> points2;
 
  for (int i = 0; i < (int) matches.size(); i++) {
    points1.push_back(keypoints_1[matches[i].queryIdx].pt);
    points2.push_back(keypoints_2[matches[i].trainIdx].pt);
  }
 
  //-- 计算本质矩阵
  Point2d principal_point(325.1, 249.7);        //相机主点, TUM dataset标定值
  int focal_length = 521;            //相机焦距, TUM dataset标定值
  Mat essential_matrix;
  essential_matrix = findEssentialMat(points1, points2, focal_length, principal_point);
 
  //-- 从本质矩阵中恢复旋转和平移信息.
  recoverPose(essential_matrix, points1, points2, R, t, focal_length, principal_point);
}

三、由R，T三角化空间坐标

第三步：根据针孔相机模型的公式，由 R,t估计特征点的空间坐标

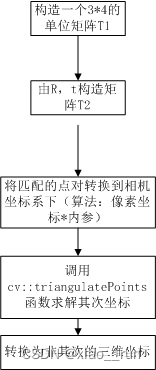
//三角化,根据匹配点和求解到的三维点。存储在points中
void triangulation(
  const vector<KeyPoint> &keypoint_1,
  const vector<KeyPoint> &keypoint_2,
  const std::vector<DMatch> &matches,
  const Mat &R, const Mat &t,
  vector<Point3d> &points) {
  Mat T1 = (Mat_<float>(3, 4) <<
    1, 0, 0, 0,
    0, 1, 0, 0,
    0, 0, 1, 0);
    //根据求解到的RT构造T2矩阵
  Mat T2 = (Mat_<float>(3, 4) <<
    R.at<double>(0, 0), R.at<double>(0, 1), R.at<double>(0, 2), t.at<double>(0, 0),
    R.at<double>(1, 0), R.at<double>(1, 1), R.at<double>(1, 2), t.at<double>(1, 0),
    R.at<double>(2, 0), R.at<double>(2, 1), R.at<double>(2, 2), t.at<double>(2, 0)
  );
  //相机内参
  Mat K = (Mat_<double>(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1);
  vector<Point2f> pts_1, pts_2;
  for (DMatch m:matches) {
    // 将像素坐标转换至相机坐标
    pts_1.push_back(pixel2cam(keypoint_1[m.queryIdx].pt, K));
    pts_2.push_back(pixel2cam(keypoint_2[m.trainIdx].pt, K));
  }
 
  Mat pts_4d;
  cv::triangulatePoints(T1, T2, pts_1, pts_2, pts_4d);
 
  // 转换成非齐次坐标
  for (int i = 0; i < pts_4d.cols; i++) {
    Mat x = pts_4d.col(i);
    x /= x.at<float>(3, 0); // 归一化
    Point3d p(
      x.at<float>(0, 0),
      x.at<float>(1, 0),
      x.at<float>(2, 0)
    );
    points.push_back(p);
  }
}

其中 triangulatePoints()的具体用法为

triangulatePoints(T1, T2, left, right, points_final) ;

Mat T1 = (Mat_<float>(3, 4) <<
		1, 0, 0, 0,
		0, 1, 0, 0,
		0, 0, 1, 0);
Mat T2 = (Mat_<float>(3, 4) <<
		R.at<double>(0, 0), R.at<double>(0, 1), R.at<double>(0, 2), T.at<double>(0, 0),
		R.at<double>(1, 0), R.at<double>(1, 1), R.at<double>(1, 2), T.at<double>(1, 0),
		R.at<double>(2, 0), R.at<double>(2, 1), R.at<double>(2, 2), T.at<double>(2, 0)
		);`
triangulatePoints(T1, T2, left, right, points_final) ;

其中T2为3x4的[R|T]矩阵，left、right为相机坐标系下的归一化坐标，
因此不能直接使用提取到的像素坐标。应首先将像素坐标通过相机内参转化到相机坐标系下。

所以通过函数pixel2cam可将像素坐标转换到归一化相机坐标系下
归一化坐标：X=(u-u0)/fx

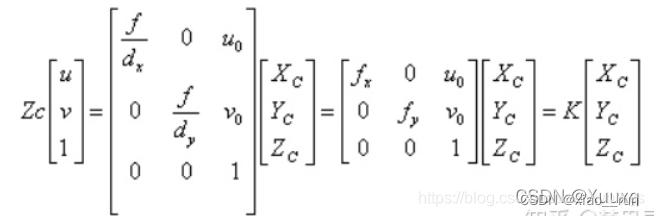
//像素坐标到归一化平面相机坐标的转换
Point2f pixel2cam(const Point2f& p, const Mat& K)
{
    return Point2f
    (
        (p.x - K.at<double>(0, 2)) / K.at<double>(0, 0),
        (p.y - K.at<double>(1, 2)) / K.at<double>(1, 1)
    );
}

四、代码demo

总的代码为：

#include <iostream>
#include <opencv2/opencv.hpp>
// #include "extra.h" // used in opencv2
using namespace std;
using namespace cv;
 
void find_feature_matches(
  const Mat &img_1, const Mat &img_2,
  std::vector<KeyPoint> &keypoints_1,
  std::vector<KeyPoint> &keypoints_2,
  std::vector<DMatch> &matches);
 
void pose_estimation_2d2d(
  const std::vector<KeyPoint> &keypoints_1,
  const std::vector<KeyPoint> &keypoints_2,
  const std::vector<DMatch> &matches,
  Mat &R, Mat &t);
 
void triangulation(
  const vector<KeyPoint> &keypoint_1,
  const vector<KeyPoint> &keypoint_2,
  const std::vector<DMatch> &matches,
  const Mat &R, const Mat &t,
  vector<Point3d> &points
);
 
/// 作图用
inline cv::Scalar get_color(float depth) {
  float up_th = 50, low_th = 10, th_range = up_th - low_th;
  if (depth > up_th) depth = up_th;
  if (depth < low_th) depth = low_th;
  return cv::Scalar(255 * depth / th_range, 0, 255 * (1 - depth / th_range));
}
 
// 像素坐标转相机归一化坐标
Point2f pixel2cam(const Point2d &p, const Mat &K);
 
int main(int argc, char **argv) {
  if (argc != 3) {
    cout << "usage: triangulation img1 img2" << endl;
    return 1;
  }
  //-- 读取图像
  Mat img_1 = imread(argv[1], CV_LOAD_IMAGE_COLOR);
  Mat img_2 = imread(argv[2], CV_LOAD_IMAGE_COLOR);
 
  vector<KeyPoint> keypoints_1, keypoints_2;
  vector<DMatch> matches;
  find_feature_matches(img_1, img_2, keypoints_1, keypoints_2, matches);
  cout << "一共找到了" << matches.size() << "组匹配点" << endl;
 
  //-- 估计两张图像间运动
  Mat R, t;
  pose_estimation_2d2d(keypoints_1, keypoints_2, matches, R, t);
 
  //-- 三角化
  vector<Point3d> points;
  //tr是三维点
  triangulation(keypoints_1, keypoints_2, matches, R, t, tr);
 
  //-- 验证三角化点与特征点的重投影关系
  Mat K = (Mat_<double>(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1);
  Mat img1_plot = img_1.clone();
  Mat img2_plot = img_2.clone();
  for (int i = 0; i < matches.size(); i++) {
    // 第一个图
    float depth1 = points[i].z;
    cout << "depth: " << depth1 << endl;
    Point2d pt1_cam = pixel2cam(keypoints_1[matches[i].queryIdx].pt, K);
    cv::circle(img1_plot, keypoints_1[matches[i].queryIdx].pt, 2, get_color(depth1), 2);
 
    // 第二个图
    Mat pt2_trans = R * (Mat_<double>(3, 1) << points[i].x, points[i].y, points[i].z) + t;
    float depth2 = pt2_trans.at<double>(2, 0);
    cv::circle(img2_plot, keypoints_2[matches[i].trainIdx].pt, 2, get_color(depth2), 2);
  }
  cv::imshow("img 1", img1_plot);
  cv::imshow("img 2", img2_plot);
  cv::waitKey();
 
  return 0;
}
 
void find_feature_matches(const Mat &img_1, const Mat &img_2,
                          std::vector<KeyPoint> &keypoints_1,
                          std::vector<KeyPoint> &keypoints_2,
                          std::vector<DMatch> &matches) {
  //-- 初始化
  Mat descriptors_1, descriptors_2;
  // used in OpenCV3
  Ptr<FeatureDetector> detector = ORB::create();
  Ptr<DescriptorExtractor> descriptor = ORB::create();
  // use this if you are in OpenCV2
  // Ptr<FeatureDetector> detector = FeatureDetector::create ( "ORB" );
  // Ptr<DescriptorExtractor> descriptor = DescriptorExtractor::create ( "ORB" );
  Ptr<DescriptorMatcher> matcher = DescriptorMatcher::create("BruteForce-Hamming");
  //-- 第一步:检测 Oriented FAST 角点位置
  detector->detect(img_1, keypoints_1);
  detector->detect(img_2, keypoints_2);
 
  //-- 第二步:根据角点位置计算 BRIEF 描述子
  descriptor->compute(img_1, keypoints_1, descriptors_1);
  descriptor->compute(img_2, keypoints_2, descriptors_2);
 
  //-- 第三步:对两幅图像中的BRIEF描述子进行匹配，使用 Hamming 距离
  vector<DMatch> match;
  // BFMatcher matcher ( NORM_HAMMING );
  matcher->match(descriptors_1, descriptors_2, match);
 
  //-- 第四步:匹配点对筛选
  double min_dist = 10000, max_dist = 0;
 
  //找出所有匹配之间的最小距离和最大距离, 即是最相似的和最不相似的两组点之间的距离
  for (int i = 0; i < descriptors_1.rows; i++) {
    double dist = match[i].distance;
    if (dist < min_dist) min_dist = dist;
    if (dist > max_dist) max_dist = dist;
  }
 
  printf("-- Max dist : %f \n", max_dist);
  printf("-- Min dist : %f \n", min_dist);
 
  //当描述子之间的距离大于两倍的最小距离时,即认为匹配有误.但有时候最小距离会非常小,设置一个经验值30作为下限.
  for (int i = 0; i < descriptors_1.rows; i++) {
    if (match[i].distance <= max(2 * min_dist, 30.0)) {
      matches.push_back(match[i]);
    }
  }
}
 
void pose_estimation_2d2d(
  const std::vector<KeyPoint> &keypoints_1,
  const std::vector<KeyPoint> &keypoints_2,
  const std::vector<DMatch> &matches,
  Mat &R, Mat &t) {
  // 相机内参,TUM Freiburg2
  Mat K = (Mat_<double>(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1);
 
  //-- 把匹配点转换为vector<Point2f>的形式
  vector<Point2f> points1;
  vector<Point2f> points2;
 
  for (int i = 0; i < (int) matches.size(); i++) {
    points1.push_back(keypoints_1[matches[i].queryIdx].pt);
    points2.push_back(keypoints_2[matches[i].trainIdx].pt);
  }
 
  //-- 计算本质矩阵
  Point2d principal_point(325.1, 249.7);        //相机主点, TUM dataset标定值
  int focal_length = 521;            //相机焦距, TUM dataset标定值
  Mat essential_matrix;
  essential_matrix = findEssentialMat(points1, points2, focal_length, principal_point);
 
  //-- 从本质矩阵中恢复旋转和平移信息.
  recoverPose(essential_matrix, points1, points2, R, t, focal_length, principal_point);
}
 
//三角化,根据匹配点和求解到的三维点。存储在points中
void triangulation(
  const vector<KeyPoint> &keypoint_1,
  const vector<KeyPoint> &keypoint_2,
  const std::vector<DMatch> &matches,
  const Mat &R, const Mat &t,
  vector<Point3d> &points) {
  Mat T1 = (Mat_<float>(3, 4) <<
    1, 0, 0, 0,
    0, 1, 0, 0,
    0, 0, 1, 0);
    //根据求解到的RT构造T2矩阵
  Mat T2 = (Mat_<float>(3, 4) <<
    R.at<double>(0, 0), R.at<double>(0, 1), R.at<double>(0, 2), t.at<double>(0, 0),
    R.at<double>(1, 0), R.at<double>(1, 1), R.at<double>(1, 2), t.at<double>(1, 0),
    R.at<double>(2, 0), R.at<double>(2, 1), R.at<double>(2, 2), t.at<double>(2, 0)
  );
  //相机内参
  Mat K = (Mat_<double>(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1);
  vector<Point2f> pts_1, pts_2;
  for (DMatch m:matches) {
    // 将像素坐标转换至相机坐标
    pts_1.push_back(pixel2cam(keypoint_1[m.queryIdx].pt, K));
    pts_2.push_back(pixel2cam(keypoint_2[m.trainIdx].pt, K));
  }
 
  Mat pts_4d;
  cv::triangulatePoints(T1, T2, pts_1, pts_2, pts_4d);
 
  // 转换成非齐次坐标
  for (int i = 0; i < pts_4d.cols; i++) {
    Mat x = pts_4d.col(i);
    x /= x.at<float>(3, 0); // 归一化
    Point3d p(
      x.at<float>(0, 0),
      x.at<float>(1, 0),
      x.at<float>(2, 0)
    );
    points.push_back(p);
  }
}
 
Point2f pixel2cam(const Point2d &p, const Mat &K) {
  return Point2f
    (
      (p.x - K.at<double>(0, 2)) / K.at<double>(0, 0),
      (p.y - K.at<double>(1, 2)) / K.at<double>(1, 1)
    );
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/985324.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

管理类联考——数学——汇总篇——知识点突破——数据分析——计数原理——减法原理除法原理

管理类联考——数学——汇总篇——知识点突破——数据分析——计数原理——减法原理除法原理

减法原理 正面难则反着做(“ − - −”号) 【思路】当出现“至少、至多”、“否定用语"等正面较难分类的题目&#xff0c;可以采用反面进行求解&#xff0c;注意部分反面的技巧以及“且、或"的反面用法。 除法原理 看到相同&#xff0c;定序用除法消序( “ &quo…
阅读更多...
JavaScript中点号运算符与方括号运算符

JavaScript中点号运算符与方括号运算符

这篇文章将介绍如何在对象中获取数据、修改数据。在JavaScript中&#xff0c;点号运算符和方括号运算符都可以用于访问对象的属性。 我们还是使用上节课的代码来演示 const ITshareArray { firstname: “张三”, secondname: “二愣子”, age: 2033-1997, job: “程序员”, fr…
阅读更多...
自动化运维——ansible (五十二) （01）

自动化运维——ansible (五十二) （01）

提示&#xff1a;文章写完后&#xff0c;目录可以自动生成&#xff0c;如何生成可参考右边的帮助文档 目录 一、概述 1.1 为什么要用自动化运维软件 1.2 自动化运维 1.3 自动化运维要注意的方面 1.4 自动化运维主要关注的方面 1.5 常见的开源自动化运维软件 1.6 自动化运维软件…
阅读更多...
Debian11安装MySQL8.0，链接Navicat

Debian11安装MySQL8.0，链接Navicat

图文小白教程 1 下载安装MySQL1.1 从MySQL官网下载安装文件1.2 安装MySQL1.3 登录MySQL 2 配置Navicat远程访问2.1 修改配置2.2 Navicat 连接 end: 卸载 MySQL 记录于2023年9月&#xff0c;Debian11 、 MySQL 8.0.34 1 下载安装MySQL 1.1 从MySQL官网下载安装文件 打开 MySQ…
阅读更多...
Unity 之 利用数组来管理资源

Unity 之 利用数组来管理资源

文章目录 在Unity中&#xff0c;资源数组&#xff08;Resource Arrays&#xff09;不是Unity的标准概念。然而&#xff0c;您可能在特定上下文中使用数组来管理资源或游戏对象。我将解释如何在Unity中使用数组来管理资源。 资源管理&#xff1a; 在Unity中&#xff0c;资源通常…
阅读更多...
9.7 C高级day2 作业

9.7 C高级day2 作业

#!/bin/bash mkdir ~/dir mkdir ~/dir/dir1 mkdir ~/dir/dir2 cp ./* ~/dir/dir1 -r cp ./*.sh ~/dir/dir2 cd ~/dir tar -cJf dir2.tar.xz dir2 mv dir2.tar.xz dir1 cd tar -xJf dir/dir1/dir2.tar.xz -C dir/dir1 tree ~/dir
阅读更多...
阿里云2核2G云服务器租用价格表_一年费用_1个月和1小时收费

阿里云2核2G云服务器租用价格表_一年费用_1个月和1小时收费

阿里云2核2G服务器多少钱一年&#xff1f;108元一年&#xff0c;折合9元一个月&#xff0c;配置为2核CPU、2G内存、3M带宽、50GB高效云盘的轻量应用服务器&#xff0c;如果是云服务器ECS&#xff0c;2核2G配置可以选择ECS通用算力型u1实例、突发性能实例t6和t5实例、密集计算型…
阅读更多...
接口响应成功未有预期结果排查

接口响应成功未有预期结果排查

最近开发中遇到一个问题&#xff0c;有一个新增接口&#xff0c;请求该接口时响应200但查询相关数据未有预期的数据&#xff0c;且日志中没有任何报错或警告&#xff1b;一般来说响应200认为是成功&#xff0c;但是结果却不符合事实&#xff1b;此时无外乎几种情况&#xff1a;…
阅读更多...
DQN算法概述及基于Pytorch的DQN迷宫实战代码

DQN算法概述及基于Pytorch的DQN迷宫实战代码

一. DQN算法概述 1.1 算法定义 Q-Learing是在一个表格中存储动作对应的奖励值&#xff0c;即状态-价值函数Q(s,a)&#xff0c;这种算法存在很大的局限性。在现实中很多情况下&#xff0c;强化学习任务所面临的状态空间是连续的&#xff0c;存在无穷多个状态&#xff0c;这种情…
阅读更多...
D361周赛复盘：模拟分割整数⭐+变为整除的最小次数⭐

D361周赛复盘：模拟分割整数⭐+变为整除的最小次数⭐

文章目录 2843.统计对称整数的数目&#xff08;模拟&#xff0c;分割整数为两部分&#xff09;思路1.整数换成字符串版本2.直接用整数的版本 2844.生成特殊数字的最小操作(模拟&#xff0c;x能被Num整除的条件)思路完整版 2843.统计对称整数的数目&#xff08;模拟&#xff0c;…
阅读更多...
4.矩阵的几何意义、变基与迹

4.矩阵的几何意义、变基与迹

文章目录 变基操作与矩阵矩阵的迹几何意义矩阵迹的几条性质 欢迎访问个人网络日志&#x1f339;&#x1f339;知行空间&#x1f339;&#x1f339; 变基操作与矩阵 我们知道空间中一点的坐标可以表示以原点为起点以该点为终点的向量。 以二维平面为例&#xff0c;如下图 选取…
阅读更多...
D1. Too Many Segments (easy version)

D1. Too Many Segments (easy version)

题目&#xff1a;样例1&#xff1a; 输入 7 2 11 11 9 11 7 8 8 9 7 8 9 11 7 9输出 3 1 4 7 样例2&#xff1a; 输入 5 1 29 30 30 30 29 29 28 30 30 30输出 3 1 2 4 样例3&#xff1a; 输入 6 1 2 3 3 3 2 3 2 2 2 3 2 3输出 4 1 3 5 6 思路&#xff1a; 这里数据范围是…
阅读更多...
React 全栈体系（四）

React 全栈体系（四）

第二章 React面向组件编程 六、组件的生命周期 1. 效果 需求:定义组件实现以下功能&#xff1a; 让指定的文本做显示 / 隐藏的渐变动画从完全可见&#xff0c;到彻底消失&#xff0c;耗时2S点击“不活了”按钮从界面中卸载组件 <!DOCTYPE html> <html lang"e…
阅读更多...
AlexNet 06

AlexNet 06

一、发展 1989年&#xff0c;Yann LeCun提出了一种用反向传导进行更新的卷积神经网络&#xff0c;称为LeNet。 1998年&#xff0c;Yann LeCun提出了一种用反向传导进行更新的卷积神经网络&#xff0c;称为LeNet-5 AlexNet&#xff0c;VGG&#xff0c;GoogleNet&#xff0c;R…
阅读更多...
863. 二叉树中所有距离为 K 的结点

863. 二叉树中所有距离为 K 的结点

863. 二叉树中所有距离为 K 的结点 C代码&#xff1a;dfs /*** struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/typedef struct {int key;struct TreeNode* node;UT_hash_handle hh; } HashTable;HashTable* head; int* ans…
阅读更多...
半导体厂务液体泄漏问题的挑战与解决方案

半导体厂务液体泄漏问题的挑战与解决方案

在半导体制造领域&#xff0c;液体泄漏是一项极具挑战性的问题。半导体工厂内有着大量的化学品、工艺液体和废水系统&#xff0c;这些液体在制造过程中扮演着至关重要的角色。然而&#xff0c;液体泄漏可能会导致严重的生产中断、环境污染和安全风险。本文将探讨半导体厂务中的…
阅读更多...
Java 多线程系列Ⅴ（常见锁策略+CAS+synchronized原理）

Java 多线程系列Ⅴ（常见锁策略+CAS+synchronized原理）

常见锁策略 一、乐观锁 & 悲观锁二、重量级锁 & 轻量级锁三、自旋锁 & 挂起等待锁四、互斥锁 & 读写锁五、可重入锁 & 不可重入锁六、公平锁 & 非公平锁七、CAS1、CAS特点2、CAS的应用3、CAS 实现自旋锁4、CAS的ABA问题 八、synchronized 原理1、synch…
阅读更多...
讯飞开放平台--星火认知大模型--开发技术文档--js实例代码详解

讯飞开放平台--星火认知大模型--开发技术文档--js实例代码详解

阿丹&#xff1a; 之前调用写过调用百度的文心一言写网站&#xff0c;讯飞的星火认知模型开放了&#xff0c;这次尝试一下使用流式来进行用户的交互。 官网&#xff1a; 平台简介 | 讯飞开放平台文档中心 星火认知大模型Web文档 | 讯飞开放平台文档中心 简介&#xff1a; 本…
阅读更多...
恒驰QA | 我们到底是做什么的？和恒大恒驰有什么关系？

恒驰QA | 我们到底是做什么的？和恒大恒驰有什么关系？

5个关键问题解答&#xff0c;带您走进恒驰信息 Q&#xff1a;恒驰信息和恒大恒驰是什么关系&#xff1f; A&#xff1a;答案是没有关系。 这是我们被问到比较频繁的问题&#xff0c;只能说纯属同名啦&#xff01;恒驰信息成立于2005年&#xff0c;比恒大恒驰创立早上14年之久。…
阅读更多...
【视觉SLAM入门】7.2. 从卡尔曼滤波到扩展卡尔曼滤波，引入、代码、原理、实战，C++实现以及全部源码

【视觉SLAM入门】7.2. 从卡尔曼滤波到扩展卡尔曼滤波，引入、代码、原理、实战，C++实现以及全部源码

"觇其平生&#xff0c;岂能容物&#xff1f;" 0. 简单认识1. 公式对比解读2. 应用举例3. 解决方案(公式---代码对应)3.1 初始化3.2 EKF3.2.1 预测---状态方程3.2.2 系统协方差矩阵3.2.3 预测---系统协方差矩阵3.2.4 设置测量矩阵3.2.5 更新---状态变量&#xff0c;卡…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023