文章目录
- 变基操作与矩阵
- 矩阵的迹
- 几何意义
- 矩阵迹的几条性质
欢迎访问个人网络日志🌹🌹知行空间🌹🌹
变基操作与矩阵
我们知道空间中一点的坐标可以表示以原点为起点以该点为终点的向量。
以二维平面为例,如下图
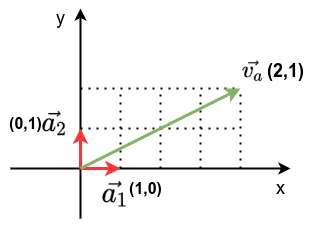
选取
a
1
⃗
=
[
1
0
]
\vec{a_1}=\begin{bmatrix}1\\0\end{bmatrix}
a1=[10]作为
x
x
x轴的基,选取
a
2
⃗
=
[
0
1
]
\vec{a_2}=\begin{bmatrix}0 \\1\end{bmatrix}
a2=[01]作为
y
y
y轴的基,建立坐标系A,则如图中的向量
v
a
⃗
\vec{v_a}
va可以表示成:
v
a
⃗
=
4
a
1
⃗
+
2
a
2
⃗
=
[
4
2
]
\vec{v_a} = 4\vec{a_1} + 2\vec{a_2}=\begin{bmatrix}4\\2\end{bmatrix}
va=4a1+2a2=[42]。
考虑上面是我们常用的建立坐标系的方式,当然可以使用其他方式建立坐标系,如
x
,
y
x,y
x,y轴不垂直(正交),
x
,
y
x,y
x,y尺度不相同都是可以的,譬如我们选择如下向量作为基
b
1
⃗
\vec{b_1}
b1和
b
2
⃗
\vec{b_2}
b2建立新的坐标系B,
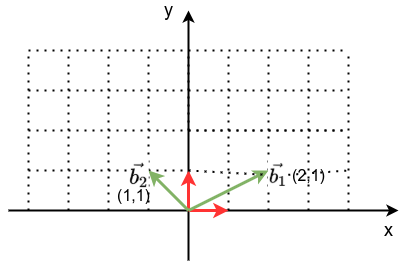
b 1 ⃗ = [ 2 1 ] \vec{b_1} = \begin{bmatrix}2\\1\end{bmatrix} b1=[21]
b 2 ⃗ = [ − 1 1 ] \vec{b_2} = \begin{bmatrix}-1\\1\end{bmatrix} b2=[−11]
则坐标系B中的一个向量
v
b
⃗
=
[
−
1
2
]
\vec{v_b}=\begin{bmatrix}-1\\2\end{bmatrix}
vb=[−12]
如下图用 b 1 ⃗ , b 2 ⃗ \vec{b_1},\vec{b_2} b1,b2可以表示为
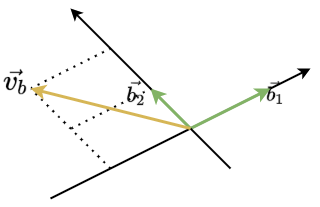
v b ⃗ = − 1 b 1 ⃗ + 2 b 2 ⃗ \vec{v_b} = -1\vec{b_1}+2\vec{b_2} vb=−1b1+2b2
如何求 v b ⃗ \vec{v_b} vb在坐标系 A A A中的表示呢?

根据
b
1
⃗
,
b
2
⃗
\vec{b_1},\vec{b_2}
b1,b2在坐标系A中的定义,
v b ⃗ A = − 1 b 1 ⃗ + 2 b 2 ⃗ = − 1 [ 2 1 ] + 2 [ − 1 1 ] = [ − 4 1 ] \vec{v_b}^A = -1\vec{b_1}+2\vec{b_2}=-1\begin{bmatrix}2\\1\end{bmatrix}+2\begin{bmatrix}-1\\1\end{bmatrix}=\begin{bmatrix}-4\\1\end{bmatrix} vbA=−1b1+2b2=−1[21]+2[−11]=[−41]
如上就得到了
v
b
⃗
\vec{v_b}
vb在A中的表示,观察上式可以写成,
v b ⃗ A = [ b 1 ⃗ b 2 ⃗ ] [ − 1 2 ] = [ b 1 ⃗ ⋅ a 1 ⃗ b 2 ⃗ ⋅ a 1 ⃗ b 1 ⃗ ⋅ a 2 ⃗ b 2 ⃗ ⋅ a 2 ⃗ ] [ − 1 2 ] = [ 2 1 1 1 ] [ − 1 2 ] \vec{v_b}^A=\begin{bmatrix}\vec{b_1}&\vec{b_2}\end{bmatrix}\begin{bmatrix}-1\\2\end{bmatrix}=\begin{bmatrix}\vec{b_1}\cdot\vec{a_1}&\vec{b_2}\cdot\vec{a_1}\\\vec{b_1}\cdot\vec{a_2}&\vec{b_2}\cdot\vec{a_2}\end{bmatrix}\begin{bmatrix}-1\\2\end{bmatrix}=\begin{bmatrix}2&1\\1&1\end{bmatrix}\begin{bmatrix}-1\\2\end{bmatrix} vbA=[b1b2][−12]=[b1⋅a1b1⋅a2b2⋅a1b2⋅a2][−12]=[2111][−12]
记
M
=
[
2
1
1
1
]
M=\begin{bmatrix}2&1\\1&1\end{bmatrix}
M=[2111]
可以发现矩阵
M
M
M表示的是将向量坐标系B变换到坐标系A中,其每一列是坐标系B的基在坐标系A中对应轴上的投影。
M
−
1
M^{-1}
M−1表示的是将向量坐标系A变换到坐标系B中。
因此从这个角度理解,矩阵表示的是线性变换矩阵。
考虑在坐标系A下发生了逆时针旋转90度的变化,对应在坐标系B是一种怎样的变化呢?
坐标系A下发生了逆时针旋转90度的变化可以写成矩阵
R
=
[
0
−
1
1
0
]
R=\begin{bmatrix}0&-1\\1&0\end{bmatrix}
R=[01−10]
将向量
v
b
⃗
\vec{v_b}
vb变换到坐标系A下为,
v a ⃗ = M v b ⃗ \vec{v_a}=M\vec{v_b} va=Mvb
则在坐标系A下发生了逆时针旋转90度后向量的坐标为
v a ′ ⃗ = R M v b ⃗ \vec{v_a'}=RM\vec{v_b} va′=RMvb
再将其变换到坐标系B下,就相当于在坐标系B下发生的与坐标系A下发生了、逆时针旋转90度等同的变化
v b ′ ⃗ = M − 1 R M v b ⃗ \vec{v_b'}=M^{-1}RM\vec{v_b} vb′=M−1RMvb
观察上式,相当于是以 R R R的每一列为基的坐标系变换到以 M M M的每一列为基的坐标系中,因此 M − 1 R M M^{-1}RM M−1RM对应的是向量的变基操作。
这里讲述的比较冗余,3Blue1Brown的视频展示的更加直观,可以直接在这里看。
矩阵的迹
几何意义
矩阵迹的定义我们都知道,是方阵对角元素的和。那么矩阵的迹有什么几何含义呢?
矩阵的迹表示矩阵的列向量在对应基向量空间上有向投影的和。
考虑一线性变换T
T
=
[
3
2
1
−
1
]
T=\begin{bmatrix}3&2\\1&-1\end{bmatrix}
T=[312−1]
这表示将在基
u
1
⃗
=
[
1
0
]
\vec{u_1}=\begin{bmatrix}1\\0\end{bmatrix}
u1=[10]
v 1 ⃗ = [ 0 1 ] \vec{v_1}=\begin{bmatrix}0\\1\end{bmatrix} v1=[01]
下的向量变换到基
u 2 ⃗ = [ 3 1 ] \vec{u_2}=\begin{bmatrix}3\\1\end{bmatrix} u2=[31]
v 2 ⃗ = [ 2 − 1 ] \vec{v_2}=\begin{bmatrix}2\\-1\end{bmatrix} v2=[2−1]
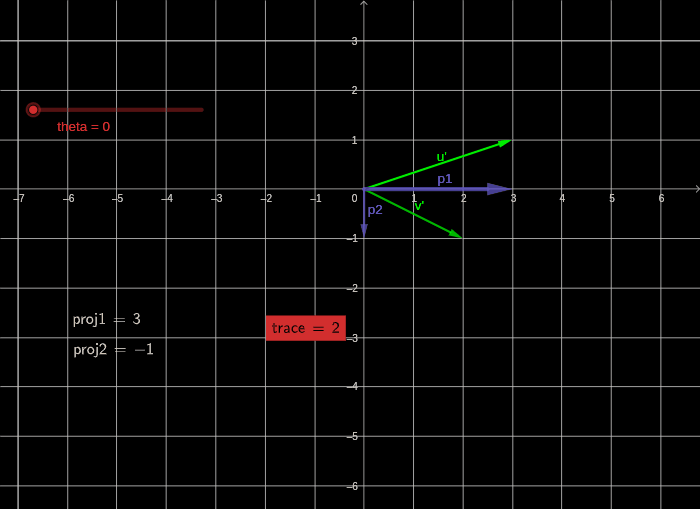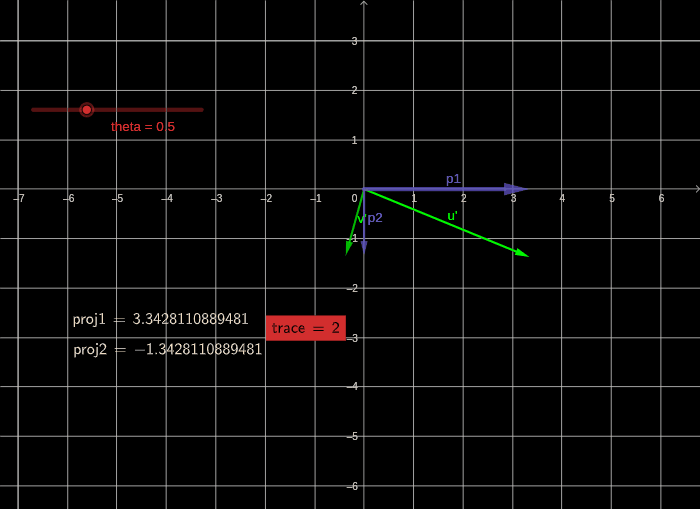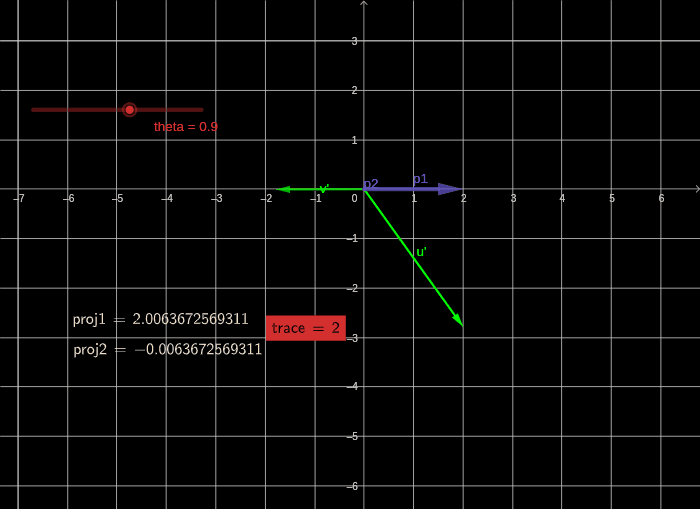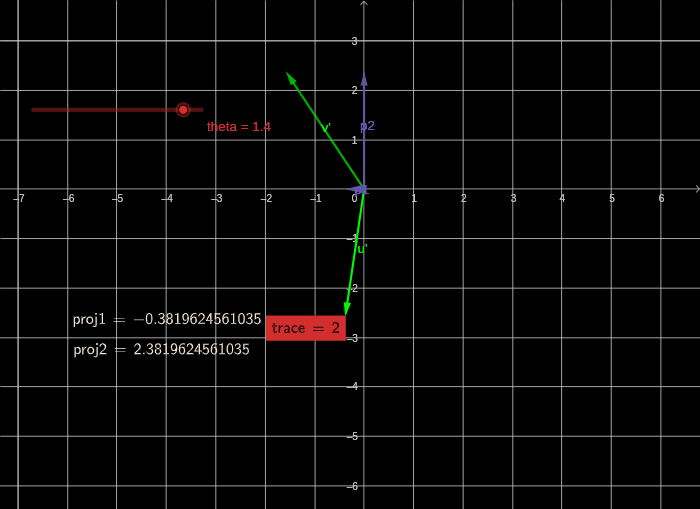
根据前面矩阵迹的定义和几何含义,看下图
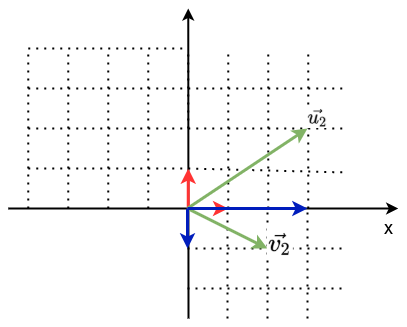
蓝色向量表示的 u 2 ⃗ , v 2 ⃗ \vec{u_2},\vec{v_2} u2,v2在 u 1 ⃗ , v 1 ⃗ \vec{u_1},\vec{v_1} u1,v1上的有向投影,
trace(T) = tr(T) = 3 + (-1) = 2
根据第一部分介绍的变基操作,当在
u
1
⃗
,
v
1
⃗
\vec{u_1},\vec{v_1}
u1,v1下逆时针旋转
θ
\theta
θ角时,对应的变换矩阵R为:
R
=
[
c
o
s
θ
−
s
i
n
θ
s
i
n
θ
c
o
s
θ
]
R=\begin{bmatrix}cos\theta&-sin\theta\\sin\theta&cos\theta\end{bmatrix}
R=[cosθsinθ−sinθcosθ]
旋转后在基 u 2 ⃗ , v 2 ⃗ \vec{u_2},\vec{v_2} u2,v2下的向量将变成
2 3 T = R − 1 T R _2^{3}T= R^{-1}TR 23T=R−1TR
2 3 T = [ 3 c o s 2 θ + 3 s i n θ c o s θ − s i n 2 θ 2 c o s 2 θ − 4 s i n θ c o s θ − 2 s i n 2 θ c o s 2 θ − 4 s i n θ c o s θ − 2 s i n 2 θ 3 s i n 2 θ − 3 s i n θ c o s θ − c o s 2 θ ] _2^{3}T=\begin{bmatrix}3cos^2\theta+3sin\theta cos\theta-sin^2\theta&2cos^2\theta-4sin\theta cos\theta-2sin^2\theta\\cos^2\theta-4sin\theta cos\theta-2sin^2\theta&3sin^2\theta-3sin\theta cos\theta-cos^2\theta\end{bmatrix} 23T=[3cos2θ+3sinθcosθ−sin2θcos2θ−4sinθcosθ−2sin2θ2cos2θ−4sinθcosθ−2sin2θ3sin2θ−3sinθcosθ−cos2θ]
计算可以求得 t r ( 2 3 T ) = 2 tr(_2^{3}T)=2 tr(23T)=2
通过上面的计算可以证明,进行纯旋转的变基操作不会改变矩阵的迹。
参考自https://saksham-malhotra2196.medium.com/geometric-meaning-of-a-trace-85ac170229f8
矩阵迹的几条性质
性质1:矩阵 A , B A,B A,B都是 K × K K\times K K×K的方阵, t r ( A + B ) = t r ( A ) + t r ( B ) tr(A+B)=tr(A)+tr(B) tr(A+B)=tr(A)+tr(B)
性质2:对矩阵乘以常数对应迹也变成常数倍, t r ( α A ) = α t r ( A ) tr(\alpha A)=\alpha tr(A) tr(αA)=αtr(A)
性质3:对于方阵A,
t
r
(
A
T
)
=
t
r
(
A
)
tr(A^T)=tr(A)
tr(AT)=tr(A)
性质4: K × L K\times L K×L矩阵A和 L × K L\times K L×K矩阵B乘积的迹满足 t r ( A B ) = t r ( B A ) tr(AB)=tr(BA) tr(AB)=tr(BA)
- 1.https://www.youtube.com/watch?v=P2LTAUO1TdA&ab_channel=3Blue1Brown
- 2.https://saksham-malhotra2196.medium.com/geometric-meaning-of-a-trace-85ac170229f8