文章目录
- 2843.统计对称整数的数目(模拟,分割整数为两部分)
- 思路
- 1.整数换成字符串版本
- 2.直接用整数的版本
- 2844.生成特殊数字的最小操作(模拟,x能被Num整除的条件)
- 思路
- 完整版
2843.统计对称整数的数目(模拟,分割整数为两部分)
给你两个正整数 low 和 high 。
对于一个由 2 * n 位数字组成的整数 x ,如果其前 n 位数字之和与后 n 位数字之和相等,则认为这个数字是一个对称整数。
返回在 [low, high] 范围内的 对称整数的数目 。
示例 1:
输入:low = 1, high = 100
输出:9
解释:在 1 到 100 范围内共有 9 个对称整数:11、22、33、44、55、66、77、88 和 99 。
示例 2:
输入:low = 1200, high = 1230
输出:4
解释:在 1200 到 1230 范围内共有 4 个对称整数:1203、1212、1221 和 1230 。
提示:
1 <= low <= high <= 10^4
思路
因为本题是计算整数每位数字的和,而整数不能直接用下标访问,所以最好将整数换为字符串,用字符串的下标进行每位数字的和累加。
字符串是字符数组,而整数并不是数组。
1.整数换成字符串版本
class Solution {
public:
bool isSymmetic(int num){
string s = to_string(num);
if(s.size()%2!=0) return false;
int firstSum=0,secondSum=0;
int middle = s.size()/2;//找到中间值
for(int i=0;i<middle;i++){
firstSum += s[i] -'0'; //一定要注意这里是字符计算,字符计算要-'0'
secondSum += s[i+middle]-'0';
}
return (firstSum==secondSum)?true:false;
}
int countSymmetricIntegers(int low, int high) {
//返回范围内的所有对称整数的数目,所以需要遍历范围内的所有i
int cnt=0;
for(int i=low;i<=high;i++){
if(isSymmetic(i)){//范围内的每一个i都需要判定
cnt++;
}
}
return cnt;
}
};
2.直接用整数的版本
如果不转换为字符串,直接用整数,就需要单独计算整数的位数,根据位数分割数字为前半部分和后半部分,用%的操作累加每一位数字。
分割数字为前半部分和后半部分的方法:
int divisor = pow(10,n/2);//n是整数的位数,也就是10的n/2次方,比如4位整数,div=10^2=100
int frontHalf = num/divisor;//直接除法/得到前半部分
int secondHalf = num%divisor;//取模%得到后半部分
div这个数字就是用来分割的,要分割成两部分,所以div = 10^(n/2),前半部分是num/div,后半部分是num%div。
分割完成之后再用%运算得到整数每一位数字。
class Solution {
public:
bool isSymmetic(int num){
//如果不转为字符串,先算位数
int n = 0;
int temp = num;
while(temp){
n++; //获取数字位数
temp/=10;
}
if(n%2!=0) return false;
//分割为前后两部分
int div = pow(10,n/2);
int first = num % div;
int second = num/div;
int sum1=0,sum2=0;
for(int i=0;i<div;i++){
sum1+=first%10;
sum2+=second%10;
first /= 10;
second /= 10;
}
return (sum1==sum2)?true:false;
}
int countSymmetricIntegers(int low, int high) {
//返回范围内的所有对称整数的数目,所以需要遍历范围内的所有i
int cnt=0;
for(int i=low;i<=high;i++){
if(isSymmetic(i)){//范围内的每一个i都需要判定
cnt++;
}
}
return cnt;
}
};
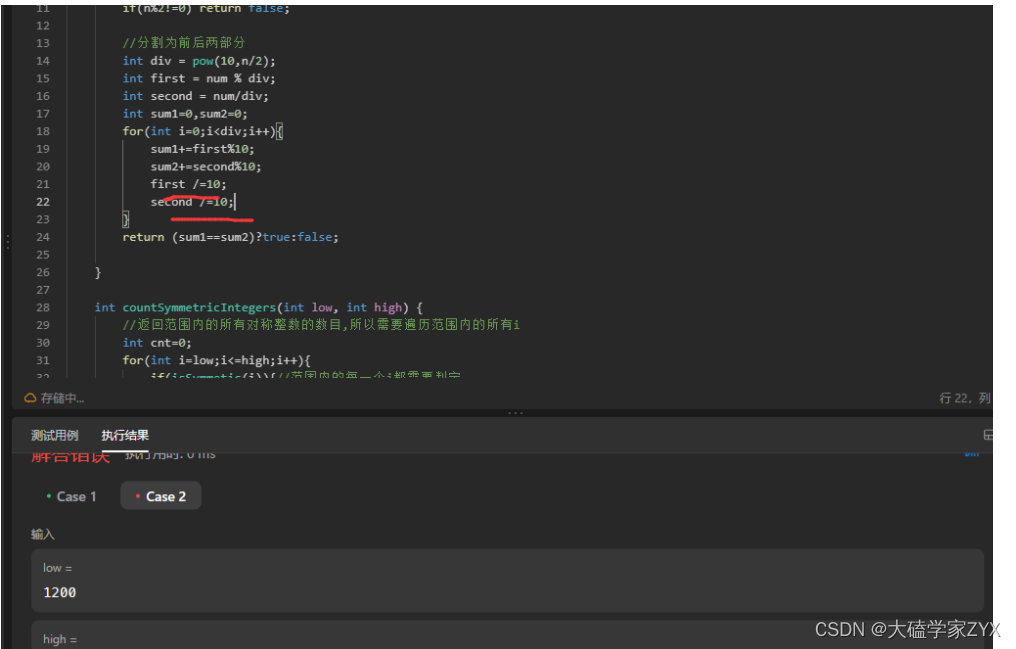
注意有的时候只过了一个用例需要检查逻辑,很可能是比较大的逻辑错误,比如下面缺了划线的两句:
2844.生成特殊数字的最小操作(模拟,x能被Num整除的条件)
给你一个下标从 0 开始的字符串 num ,表示一个非负整数。
在一次操作中,您可以选择 num 的任意一位数字并将其删除。请注意,如果你删除 num 中的所有数字,则 num 变为 0。
返回最少需要多少次操作可以使 num 变成特殊数字。
如果整数 x 能被 25 整除,则该整数 x 被认为是特殊数字。
示例 1:
输入:num = "2245047"
输出:2
解释:删除数字 num[5] 和 num[6] ,得到数字 "22450" ,可以被 25 整除。
可以证明要使数字变成特殊数字,最少需要删除 2 位数字。
示例 2:
输入:num = "2908305"
输出:3
解释:删除 num[3]、num[4] 和 num[6] ,得到数字 "2900" ,可以被 25 整除。
可以证明要使数字变成特殊数字,最少需要删除 3 位数字。
示例 3:
输入:num = "10"
输出:1
解释:删除 num[0] ,得到数字 "0" ,可以被 25 整除。
可以证明要使数字变成特殊数字,最少需要删除 1 位数字。
提示
1 <= num.length <= 100num仅由数字'0'到'9'组成num不含任何前导零
思路
本题求的是删成特殊数字的最小次数,重点是x被25整除的等价条件。x能被25整除,那么说明最靠后的位置是00、25、50、75。或者是一个单独的数字0(比如示例3,针对数字位数本来就比较小的情况)。
我们可以直接倒序遍历,并且用布尔值记录之前的遍历中有没有碰到可以和当前数字(0/2/5/7)组成一对儿的数。
如果整个遍历完成了,都不存在成对的00/25/50/75,但是有一个0的话,答案就是n-1。(0可以不删掉)
完整版
class Solution {
public:
int minimumOperations(string num) {
bool f0 = false,f5=false;
int n=num.size();
for(int i=n-1;i>=0;i--){
if(num[i]=='0'){
//检查之前有没有0
if(f0) return n-1-i-1;
f0 = true; //记录当前的0
}
else if(num[i]=='5'){
if(f0) return n-1-i-1;
f5 = true; //记录当前的5
}
else if(num[i]=='2'||num[i]=='7'){
if(f5) return n-i-2;
}
}
//所有的遍历都结束之后,都没返回,但是有一个0
if(f0) return n-1;
return n;
}
};
总结来说就是要知道x能被num整除的等价条件,然后用布尔值记录倒着遍历过的数字,最后如果都没有但是有一个0,也需要考虑。