目录

1.B树的引入

2.B树的概念

3.B树是如何插入的？

4.具体的代码实现

1.B树的引入

在以往我们在内存中搜索数据时，可以使用红黑树，平衡树，哈希表等数据结构，但是当数据量比较大，不能一次放进内存，只能放在磁盘上，需要搜索数据的时候如何处理？

这时如果用其他的数据结构：

    - 平衡二叉搜索树需要logN次，在磁盘访问中仍然是很慢的

    - 使用哈希表，在极端场景下，哈希冲突很多，效率下降很多

如何加速数据的查找速度？

        我们可以考虑将存放关键字及其映射的数据的地址放到一个内存中的搜索树的节点中，那么要访问数据时，先取这个地址去磁盘访问数据。首先，对于磁盘而言：磁盘定位到一页的信息并将其从中读出，要比读出信息进行检查的时间要长的多。如果能提高定位速度，便能有效提高访问速度，于是降低平衡树的高度便是可选之举，1970年，R.Bayer和E.mccreight提出了一种适合外查找的树，它是一种平衡的多叉树，称为B树。

2.B树的概念

首先认识B树：B树是一棵平衡的M路平衡搜索树，可以是空树或者满足下面的性质：

template<class K, size_t M>//K 是键值，M是树的分支数
struct BTreeNode
{
	K _key[M-1];//存储关键字的数组
	BTreeNode<K, M>* _subs[M];//存储子树根节点指针的指针数组
	size_t _n;//已经存储的关键字的个数
};

    void InOrder()
	{
		_InOrder(_root);
	}

private:
	void _InOrder(Node* root)
	{
		if (root == nullptr)
			return;
		int i = 0;
		for (; i < root->_n; i++)
		{
			_InOrder(root->_subs[i]);
			cout << root->_key[i] << " ";
		}
		_InOrder(root->_subs[i]);
	}

3.B树是如何插入的？

 插入分析：

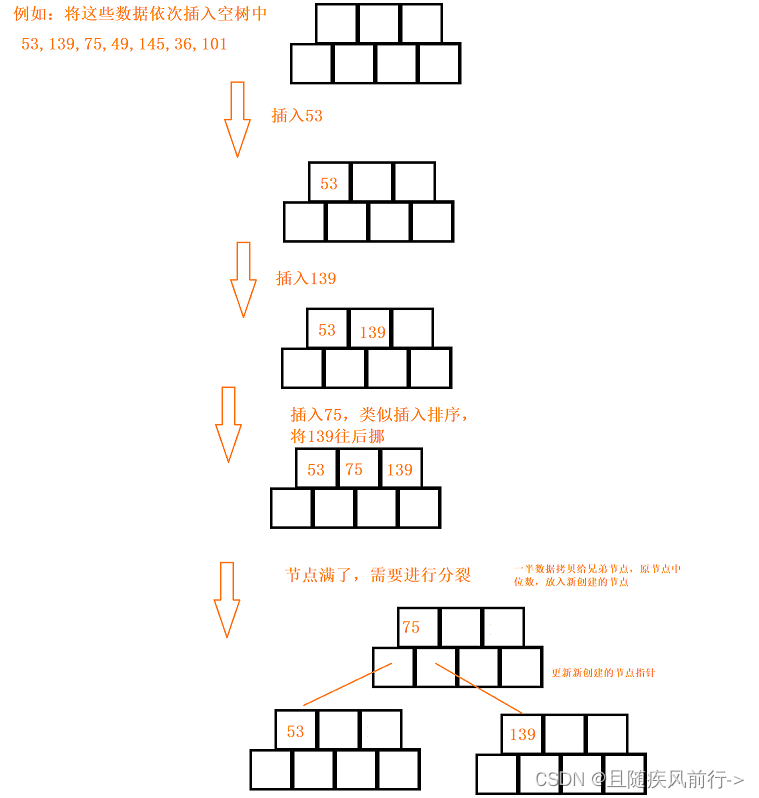
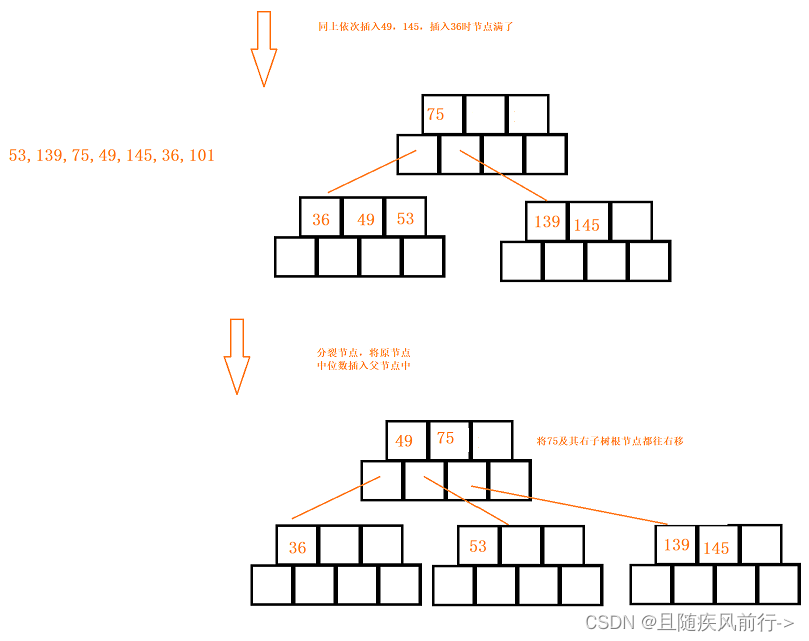
        依次插入元素（类似搜索树的查找规则，新增的数据都要插入在叶子节点上），节点满了就进行分裂，将节点右边一半的数据拷贝给兄弟节点，将本来节点的中位数往上向父亲的节点插入，并往父亲节点插入一个兄弟节点指针，如果是根节点分裂，就再创建一个根节点。

        从B树的插入可以看出B树是天然平衡的，因为插入操作本质是整棵树向右生长和向上生长都是没有产生高度差的。

以一些数据的插入为例：

4.具体的代码实现

#pragma once
#include<utility>
using namespace std;

template<class K,size_t M>//K 是键值，M是树的分支数
struct BTreeNode
{
	//为了方便插入满了之后分裂,两个数组都多开一个空间
	K _key[M];//存储关键字的数组
	BTreeNode<K, M>* _subs[M + 1];//存储子树根节点指针的指针数组
	BTreeNode<K, M>* _parent;//存储父节点指针，方便分裂时更新
	size_t _n;//已经存储的关键字的个数
	BTreeNode()
	{
		for (size_t i = 0; i < M; i++)
		{
			_key[i] = K();
			_subs[i] = nullptr;
		}
		_subs[M] = nullptr;
		_parent = nullptr;
		_n = 0;
	}
};

template<class K,size_t M>
class BTree
{
	typedef BTreeNode<K, M> Node;
private:
	Node* _root = nullptr;

public:
	pair<Node*, int> Find(const K& key)
	{
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			size_t i = 0;
			while (i < cur->_n)
			{
				if (key < cur->_key[i])
					break;
				else if (key > cur->_n)
					++i;
				else
					return make_pair(cur, i);
			}
			parent = cur;
			cur = cur->_subs[i];//相当于往左子树跳转
		}
		return make_pair(parent, -1);//-1 表示 没有找到key
	}

	void InsertKey(Node* node, const K& key, Node* child)
	{
		int end = node->_n-1;
		while (end >= 0)
		{
			if (node->_key[end] > key)
			{
				node->_key[end + 1] = node->_key[end];
				node->_subs[end + 2] = node->_subs[end + 1];
				--end;
			}
			else break;
		}
		node->_key[end + 1] = key;
		node->_subs[end + 2] = child;
		if (child)child->_parent = node;
		node->_n++;
	}

	bool Insert(const K& key)
	{
		if (_root == nullptr)
		{
			_root = new Node;
			_root->_key[0] = key;
			_root->_n++;
			return true;
		}

		pair<Node*, int>ret = Find(key);
		if (ret.second >= 0)
			return false;

		Node* parent = ret.first;//find返回了需要插入的节点所在位置
		//插入满了，分裂，往上更新时，需要往父亲节点插入key 和 brother指针
		K newkey = key;
		Node* child = nullptr;
		while (1)
		{
			InsertKey(parent, newkey, child);
			if (parent->_n < M)
				return true;
			else
			{
				size_t mid = M / 2;
				//拷贝[mid+1,M-1]给兄弟节点
				Node* brother = new Node;
				int i = mid + 1;
				int j = 0;
				for (; i < M; i++)
				{
					brother->_key[j] = parent->_key[i];
					if (parent->_subs[i])
					{
						brother->_subs[j] = parent->_subs[i];
						parent->_subs[i]->_parent = brother;
					}
					++j;
				}
				if (parent->_subs[i])
				{
					brother->_subs[j] = parent->_subs[i];//最右边的指针
					parent->_subs[i]->_parent = brother;
				}

				//更新_n;
				brother->_n = j;
				parent->_n -= brother->_n + 1;

				K midkey = parent->_key[mid];
				if (parent->_parent == nullptr)//说明刚才分裂的节点是根节点
				{
					_root = new Node;
					_root->_n++;
					_root->_key[0] = midkey;
					_root->_subs[0] = parent;
					_root->_subs[1] = brother;
					parent->_parent = brother->_parent = _root;
					break;
				}
				else//parent继续往上跳，更新父亲节点
				{
					newkey = midkey;
					parent = parent->_parent;
					child = brother;
				}
			}
		}
		return true;
	}

	void InOrder()
	{
		_InOrder(_root);
	}

private:
	void _InOrder(Node* root)
	{
		if (root == nullptr)
			return;
		int i = 0;
		for (; i < root->_n; i++)
		{
			_InOrder(root->_subs[i]);
			cout << root->_key[i] << " ";
		}
		_InOrder(root->_subs[i]);
	}
};