目录
7.9 递归
7.9.1 包含一个递归调用的递归
7.9.2 包含多个递归调用的递归
7.9 递归
下面介绍一些完全不同的内容。C++函数有一种有趣的特点——可以调用自己(然而,与C语言不同的是,C++不允许main()调用自己),这种功能被称为递归。尽管递归在特定的编程(例如人工智能)中是一种重要的工具,但这里只简单地介绍一下它是如何工作的。
7.9.1 包含一个递归调用的递归
如果递归函数调用自己,则被调用的函数也将调用自己,这将无限循环下去,除非代码中包含终止调用链的内容。通常的方法将递归调用放在if语句中。例如,void类型的递归函数recurs()的代码如下:
void recurs(argumentlist)
{
statements1
if(test)
recurs(arguments)
statements2
}
test最终将为false,调用链将断开。
递归调用将导致一系列有趣的事件。只要if语句为true,每个recurs()调用都将执行statements1,然再调用recurs(),而不会执行statements2。当if语句为false时,当前调用将执行statements2。当前调用结束后,程序控制权将返回调用它的recurs(),而该recurs()将执行其statements2部分,然后结束,并将控制权返回给前一个调用,依此类推。因此,如果recurs()进行了5次递归调用,则第一个statements1部分将按函数调用的顺序执行5次,然后statements2部分将以与函数调用相反的顺序执行5次。进入5层递归后,程序将沿进入的路径返回。程序清单7.16演示了这种行为。
程序清单7.16 recur.cpp
//recur.cpp -- using recursion
#include<iostream>
void countdown(int n);
int main()
{
countdown(4); //call the recursive function
return 0;
}
void countdown(int n)
{
using namespace std;
cout << "Counting down ... " << n << endl;
if (n > 0)
countdown(n - 1); //function calls itself
cout << n << ": Kaboom!\n";
}下面是该程序的输出:
Counting down ... 4 <level 1; adding levels of recursion
Counting down ... 3 <level 2;
Counting down ... 2 <level 3;
Counting down ... 1 <level 4;
Counting down ... 0 <level 5; final recursive call
0: Kaboom! <level 5; beginning to back out
1: Kaboom! <level 4;
2: Kaboom! <level 3;
3: Kaboom! <level 2;
4: Kaboom! <level 1;
注意,每个递归调用都创建自己的一套变量,因此当程序到达第5次调用时,将有5个独立的n变量,其中每个变量的值都不同。为验证这一点,读者可以修改程序清单7.16,使之显示n的地址和值:
cout << "Counting down ... " << n << " (n at " << &n << ")" << endl;
...
cout << n << ": Kaboom!"<< " (n at " << &n << ")" << endl;
经过上述修改后,该程序的输出将与下面类似:
Counting down ... 4 (n at 00EFF744)
Counting down ... 3 (n at 00EFF66C)
Counting down ... 2 (n at 00EFF594)
Counting down ... 1 (n at 00EFF4BC)
Counting down ... 0 (n at 00EFF3E4)
0: Kaboom! (n at 00EFF3E4)
1: Kaboom! (n at 00EFF4BC)
2: Kaboom! (n at 00EFF594)
3: Kaboom! (n at 00EFF66C)
4: Kaboom! (n at 00EFF744)
注意,在一个内存单元(内存地址为0012FE0C),存储的n值为4;在另一个内存单元(内存地址为0012FD34),存储的n值为3;等等。另外,注意到在Counting down阶段和Kaboom阶段的相同层级,n的地址相同。
7.9.2 包含多个递归调用的递归
在需要将一项工作不断分为两项较小的、类似的工作时,递归非常有用。例如,请考虑使用这种方法来绘制标尺的情况。标出两端,找到中点并将其标出。然后将同样的操作用于标尺的左半部分和右半部分。如果要进一步细分,可将同样的操作用于当前的每一部分。递归方法有时被称为分而治之策略(divide-and-conquer strategy)。程序清单7.17使用递归函数subdivide()演示了这种方法,该函数使用一个字符串,该字符串除两端为|字符外,其他全部为空格。main函数使用循环调用subdivide()函数6次,每次将递归层编号加1,并打印得到的字符串。这样,每行输出表示一层递归。该程序使用限定符std::而不是编译指令using,以提醒读者还可以采取这种方式。
程序清单7.17 ruler.cpp
//ruler.cpp -- using recursion to subdivide a ruler
#include<iostream>
const int Len = 66;
const int Divs = 6;
void subdivide(char ar[], int low, int high, int level);
int main()
{
char ruler[Len];
int i;
for (i = 1; i < Len - 2; i++)
ruler[i] = ' ';
ruler[Len - 1] = '\0';
int max = Len - 2;
int min = 0;
ruler[min] = ruler[max] = '|';
std::cout << ruler << std::endl;
for (i = 1; i < Divs; i++)
{
subdivide(ruler, min, max, i);
std::cout << ruler << std::endl;
for (int j = 1; j < Len - 2; j++)
ruler[j] = ' '; //reset to blank ruler
}
return 0;
}
void subdivide(char ar[], int low, int high, int level)
{
if (level == 0)
return;
int mid = (high + low) / 2;
ar[mid] = '|';
subdivide(ar, low, mid, level - 1);
subdivide(ar, mid, high, level - 1);
}下面是程序清单7.17中程序的输出:
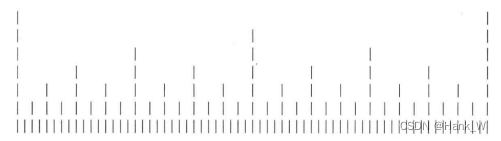
程序说明
在程序清单7.17中,subdivide()函数使用变量level来控制递归层。函数调用自身时,将把level减1,当level为0时,该函数将不再调用自己。注意,subdivide()调用自己两次,一次针对左半部分,另一次针对右半部分。最初的中点被用作一次调用的右端点和另一次调用的左端点。请注意,调用次数将呈几何级数增长。也就是说,调用一次导致两个调用,然后导致4个调用,再导致8个调用,依此类推。这就是6层调用能够填充64个元素的原因(26=64)。这将不断导致函数调用数(以及存储的变量数)翻倍,因此如果要求的递归层数很多,这种递归方式将是一种糟糕的选择;然而,如果递归层次较少,这将是一种精致而简单的选择。