改进后的dijkstra算法

利用小根堆

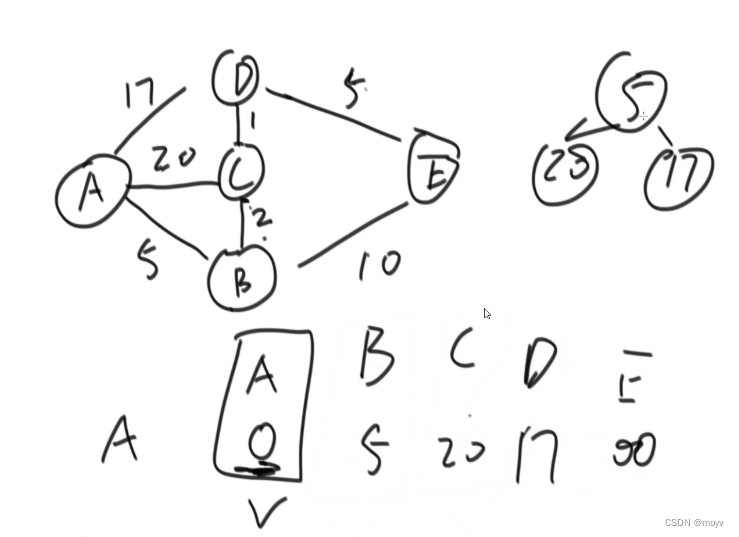
将小根堆特定位置更改，再改成小根堆

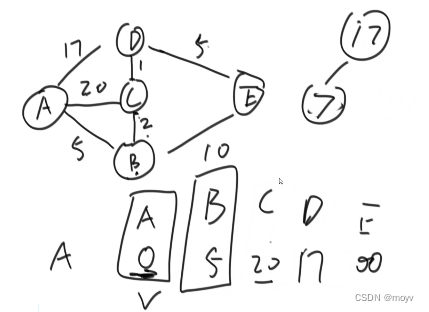
nodeHeap.addOrUpdateOrIgnore(edge.to, edge.weight + distance);

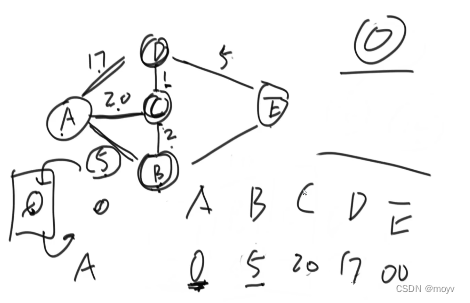
//改进后的dijkstra算法
//从head出发，所有head能到达的节点，生成到达每个节点的最小路径记录并返回
public static HashMap<Node, Integer> dijkstra2(Node head, int size) {
   
	NodeHeap nodeHeap = new NodeHeap(size);
	nodeHeap.addOrUpdateOrIgnore(head, 0);//如果有一个结点的记录是第一次出现，要记录下来，小于update，大于ignore
	HashMap<Node, Integer> result = new HashMap<>();
	while (!nodeHeap.isEmpty()) {
   
		NodeRecord record = nodeHeap.pop();//record:head到node的最短距离
		Node cur = record.node;
		int distance = record.distance;
		for (Edge edge : cur.edges) {
   
			nodeHeap.addOrUpdateOrIgnore(edge.to, edge.weight + distance);//见图3
		}
		result.put(cur, distance);
	}
	return result;
}

public static class NodeRecord {
   
		public Node node;
		public int distance;

		public NodeRecord(Node node, int distance) {
   
			this.node = node;
			this.distance = distance;
		}
	}

public static class NodeHeap {
   
	private Node[] nodes;
	private HashMap<Node, Integer> heapIndexMap;//记录node在哪个位置上
	private HashMap<Node, Integer> distanceMap;//node到head的最短距离
	private int size;//堆上一共有多少个结点

	public NodeHeap(int size) {
   
		nodes = new Node[size];
		heapIndexMap = new HashMap<>();
		distanceMap = new HashMap<>();
		this.size = 0;
	}

	public boolean isEmpty() {
   
		return size == 0;
	}

	public void addOrUpdateOrIgnore(Node node, int distance) {
   
		if (inHeap(node)) {
   //在堆里
			distanceMap.put(node, Math.min(distanceMap.get(node), distance));//之前的距离和现在的距离用小的
			insertHeapify(node, heapIndexMap.get(node));//向上堆化，根据distanceMap决定一个值上下
		}
		if (!isEntered(node)) {
   //没有进过
			nodes[size] = node;
			heapIndexMap.put(node, size);
			distanceMap.put(node, distance);
			insertHeapify(node, size++);//向上调整
		}
		//进来过没在堆里，ignore
	}

	public NodeRecord pop() {
   
		NodeRecord nodeRecord = new NodeRecord(nodes[0], distanceMap.get(nodes[