前言
思索了很久到底要不要出深度学习内容,毕竟在数学建模专栏里边的机器学习内容还有一大半算法没有更新,很多坑都没有填满,而且现在深度学习的文章和学习课程都十分的多,我考虑了很久决定还是得出神经网络系列文章,不然如果以后数学建模竞赛或者是其他更优化模型如果用上了神经网络(比如利用LSTM进行时间序列模型预测),那么就更好向大家解释并且阐述原理了。但是深度学习的内容不是那么好掌握的,包含大量的数学理论知识以及大量的计算公式原理需要推理。且如果不进行实际操作很难够理解我们写的代码究极在神经网络计算框架中代表什么作用。不过我会尽可能将知识简化,转换为我们比较熟悉的内容,我将尽力让大家了解并熟悉神经网络框架,保证能够理解通畅以及推演顺利的条件之下,尽量不使用过多的数学公式和专业理论知识。以一篇文章快速了解并实现该算法,以效率最高的方式熟练这些知识。
现在很多竞赛虽然没有限定使用算法框架,但是更多获奖的队伍都使用到了深度学习算法,传统机器学习算法日渐式微。比如2022美国大学生数学建模C题,参数队伍使用到了深度学习网络的队伍,获奖比例都非常高,现在人工智能比赛和数据挖掘比赛都相继增多,对神经网络知识需求也日渐增多,因此十分有必要掌握各类神经网络算法。
博主专注建模四年,参与过大大小小数十来次数学建模,理解各类模型原理以及每种模型的建模流程和各类题目分析方法。此专栏的目的就是为了让零基础快速使用各类数学模型、机器学习和深度学习以及代码,每一篇文章都包含实战项目以及可运行代码。博主紧跟各类数模比赛,每场数模竞赛博主都会将最新的思路和代码写进此专栏以及详细思路和完全代码。希望有需求的小伙伴不要错过笔者精心打造的专栏。

上篇文章本来是打算完结神经网络的,忘记了写的是基于梯度的反向传播的计算,并不是基于激活函数误差的反向传播的神经网络。对于数据微分来说,它的计算非常消耗时间,会导致epoch迭代数据传播效率低下,自然导致训练准确率低。如果对误差反向传播较为熟悉的话,就没有必要用数值微分,故掌握误差反向传播需要掌握的比较熟练。

我们仍然从基础原理一步一步来理解反向传播的计算方法,这样一来基础比较扎实且容易明白。
一、ReLU反向传播实现
激活函数我们有对ReLU基本了解:
ReLU(Rectified Linear Activation)函数是深度学习中常用的非线性激活函数之一。它在神经网络中广泛应用,因为它简单有效,能够解决梯度消失问题,并且在实际应用中取得了良好的结果。
ReLU 函数的定义很简单:对于任何输入值 x,输出等于输入 x(如果 x 大于等于零),或者输出为零(如果 x 小于零)。数学表达式如下:

也就是说如果前向传播的输入大于0,则直接传给下一层;如果为0则直接传给下一层。
通过上述描述,我们可以求出y关于x的导数:
那么ReLU的反向传播为的实现代码为:
class Relu:
def __init__(self):
self.x=None
def forward(self,x):
self.x = np.maximum(0,x)
out = self.x
return out
def backward(self,dout):
dx = dout
dx[self.x <= 0]=0
return dx是不是比较好理解,方向传播即为原计算方程进行偏导,那么我们再来看看Sigmoid的反向传播。
二、Sigmoid反向传播
Sigmoid函数公式我们知道为:
,通常用于二元分类模型。
这里推荐一本书能够更加系统基础的学习神经网络:深度学习与图像识别:原理与实践
里面有很详细的推导过程,这里借用书上Sigmoid计算图来展示:

那么对于反向传播我们需要反着来推,从右向左依次来看:
- 对
进行求偏导,不知道大家大学高数学得怎么样了,对其求偏导为
- 第二步进行反响传播时,会将上游的值
乘以本阶段的导数,对于
求导得到的导数为
,故第二步的导数为
- 第三步
求导自然是-1.故最终求导为
,之后乘以上层求导结果,输出为
.
最后我们Python实现一下:
class _sigmoid:
def __init__(self):
self.out = None
def forward(self,x):
out = 1/(1+np.exp(-x))
self.out=out
return out
def backward(self,dout):
dx = dout*self.out*(1-self.out)
return dx三、Affine层
神经网络中的 Affine 层(也称为全连接层或线性层)在神经网络中扮演着重要的角色,其主要作用是引入线性变换和权重参数。这一层在前馈神经网络中用于将输入数据与权重相乘,然后加上偏置,从而产生输出。
Affine通常被加在卷积神经网络或循环神经网络中作为最终预测前的输出的顶层。一般形式为:
,其中x是层输入,w是参数,b是一个偏置量,f是一个非线性激活函数。
这里需要注意的是X基本为多个,也就是矩阵。如果加上1偏置量的话,偏置量会被加到各个X-W中去。
class Affine:
def __init__(self,W,b):
self.W=W
self.b=b
self.x=None
self.dW=None
self.db=None
def forward(self,x):
self.x=x
out=np.dot(x,self.W)+self.b
return out
def backward(self,dout):
dx = np.dot(dout,self.W.T)
self.dW = np.dot(self.x.T,dout)
self.db = np.sum(dout,axis=0)
return dx四、基于数值微分和误差反向传播的比较
我们现在接触了两种梯度计算的方法:一种是基于数值微分的方法,另一种是基于误差反向传播的方法,对于数值微分来说,计算消耗是比较大的,用时很长。所以一般都是推荐使用误差反向传播,具体代码如下:
from collections import OrderedDict
import numpy as np
class TwoLayerNet:
def __init__(self,input_size,hidden_size,output_size,weight_init_std = 0.01):
#权重
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size,hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size,output_size)
self.params['b2'] = np.zeros(output_size)
#生成层
self.layers = OrderedDict()
self.layers['Affine1'] = Affine(self.params['W1'],self.params['b1'])
self.layers['Relu1'] = Relu()
self.layers['Affine2'] = Affine(self.params['W2'],self.params['b2'])
self.layers['Relu2'] = Relu()
self.lastLayer = SoftmaxWithLoss()
def predict(self,x):
for layer in self.layers.values():
x = layer.forward(x)
return x
#x:输入数据,y:监督数据
def loss(self,x,y):
p = self.predict(x)
return self.lastLayer.forward(p,y)
def accuracy(self,x,y):
p = self.predict(x)
p = np.argmax(y,axis=1)
if y.ndim != 1:
y = npp.argmax(y,axis=1)
accuracy = np.sum(p==y)/float(x.shape[0])
return accuracy
#x:输入数据,y:监督数据
def numerical_gradient(self,x,y):
loss_W = lambda W: self.loss(x,y)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
def gradient(self , x, y):
#forward
self.loss(x,y)
#backward
dout = 1
dout = self.lastLayer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
#设定
grads = {}
grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
return grads
network = TwoLayerNet(input_size = 784,hidden_size = 50 , output_size = 10)
x_batch = x_train[:100]
y_batch = y_train[:100]
grad_numerical = network.numerical_gradient(x_batch,y_batch)
grad_backprop = network.gradient(x_batch,y_batch)
for key in grad_numerical.keys():
diff = np.average(np.abs(grad_backprop[key]-grad_numerical[key]))
print(key+":"+str(diff))
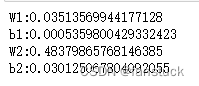
两者差值并不是很大,那么我们再看看准确率:
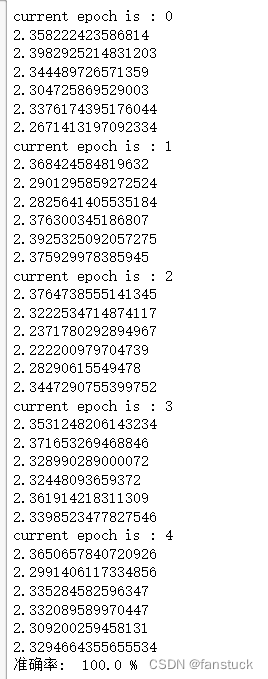
是不是感觉很厉害了,那么到这里神经网络基础内容就结束了,我们完成了从输入层-前向传播-权重偏置-激活函数-反向传播-前向传播----....网络的计算框架搭建,基本内容已经掌握了。那么我们现在可以开启深度学习网络的深入研究了,敬请期待下篇文章内容。