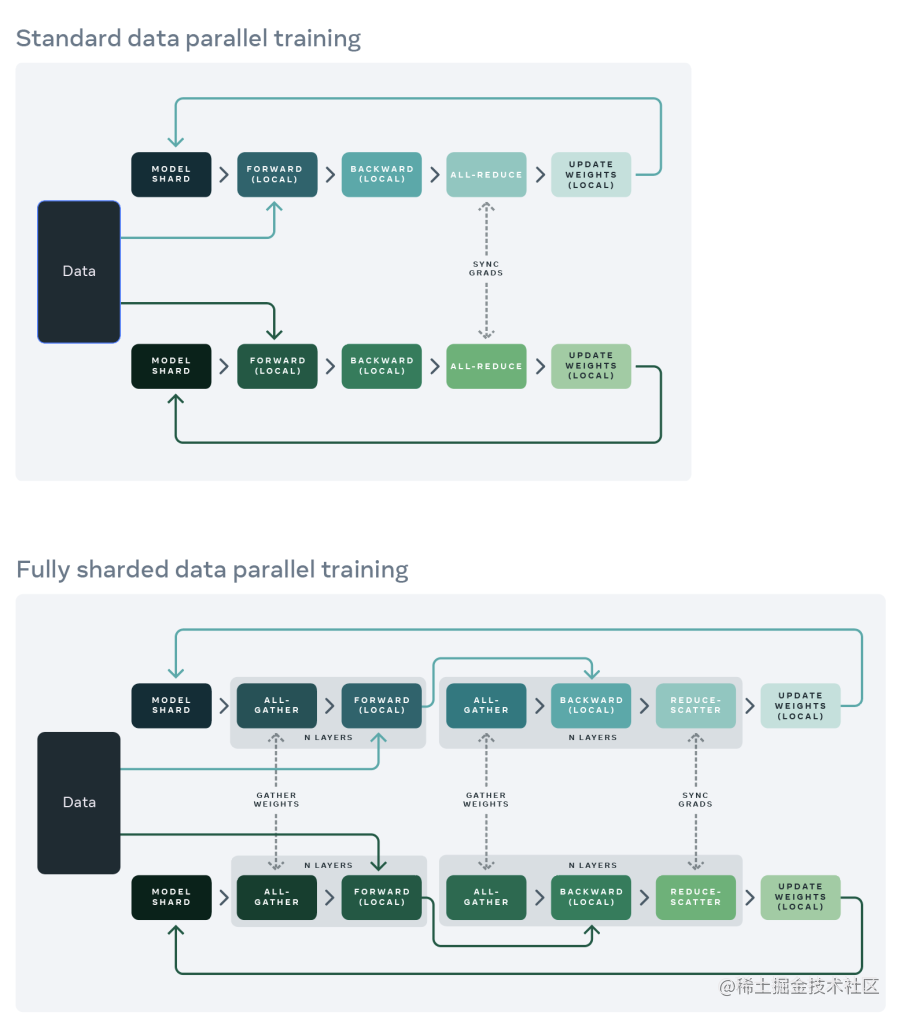
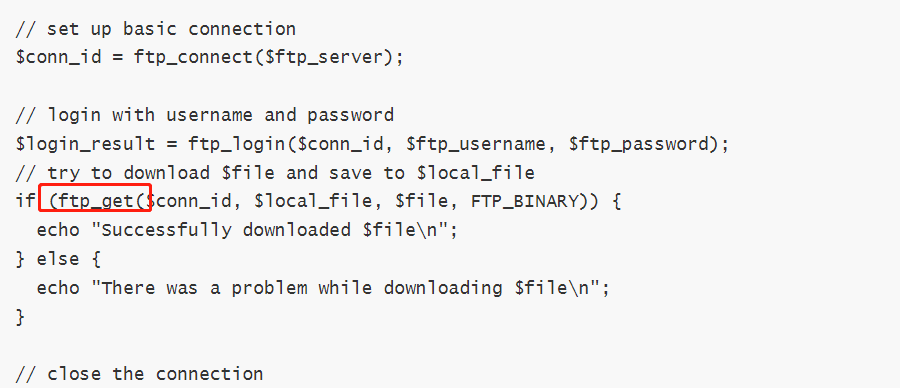
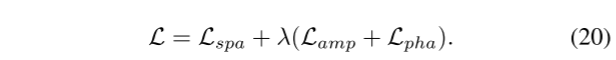问题：

conda之前安装的默认路径空间满了没法进行安装，为此将其进行迁移，但是迁移之后报错

bash: /data/anaconda3/bin/conda: /home/anaconda3/bin/python: 坏的解释器: 没有那个文件或目录

解决方案：

1、修改~/.bashrc中的环境变量，将conda的相关路径修改成最新的

vim ~/.bashrc

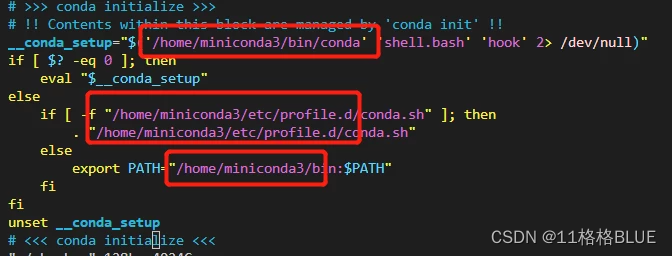
修改完使其生效

source ~/.bashrc

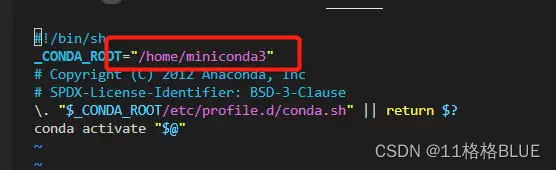
2、vim /home/miniconda3/bin/activate

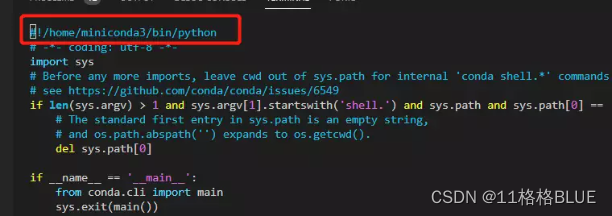
3、vim /home/miniconda3/bin/conda

4、vim /home/miniconda3/bin/pip

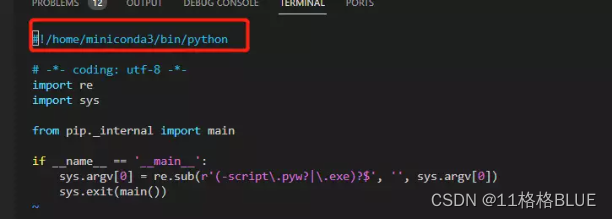
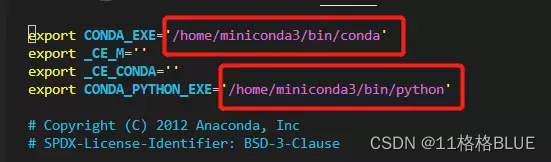
5、vim /home/miniconda3/etc/profile.d/conda.sh

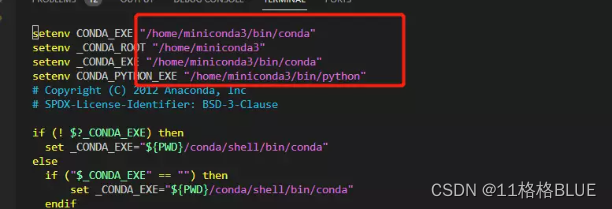
6、vim /home/miniconda3/etc/profile.d/conda.csh

7、修改虚拟环境中的pip和pip3

cd /home/chenan/miniconda3/envs/yolo_slowfast/bin
vim pip
vim pip3