大家好，我是比特桃。本系列笔记只专注于探讨研究区块链技术原理，不做其他违反相关规定的讨论。 区块链技术已被纳入国家十四五规划，在“加快数字发展建设数字中国”篇章中，区块链被列为“十四五”七大数字经济重点产业之一，迎来创新发展新机遇。

经科技部批复，国家区块链技术创新中心落地北京中关村国家自主创新示范区，并于2023年5月10日正式投入运行。

一、密码学基础

在中本聪撰写的《比特币：一种点对点的电子现金系统》中，就对密码学在区块链交易系统中的作用有着很好的诠释：用户的账户或者资产在区块链上就是使用密码学中数字签名算法的公钥进行表示的，可以这样说：拥有这个公钥对应私钥的人就对相应的账户或资产拥有控制权；当要将数字资产发送给下一个拥有者时，就需要使用对应私钥对整个交易进行数字签名，区块链的其他使用者通过公钥验证数字签名的合法性，从而可以确认该次转账是否经过资产所有者授权。

又比如在以太坊中的智能合约的地址就是SHA3哈希算法生成的，甚至就连合约状态存储的时候也用到SHA3散列算法，可以这样说密码学知识已经渗透到了区块链的方方面面。本文不会深入挖掘各个算法的具体的实现，只要理解在区块链系统中我们面临哪些问题，利用密码学的知识又是如何解决这些问题的即可。

从区块链整体框架来看，通过本文可以了解到如何在节点间建立一个安全的物理连接，保证节点间数据可信的传输，这也是区块链信任机器最基本的基石，同时也为后面涉及密码学相关的技术作为铺垫。

想象一下，如果我们不采用任何技术手段，在一条不加密的网络链路上传输信息可能会面临哪些问题呢？

窃听风险：黑客可能监听双方的通信链路，偷听双方的通信内容。
篡改风险：黑客可以随意修改双方的通信内容，双方无法正确的传递消息。
冒充风险：黑客可以冒充任意一个人的身份参与通信。

可以看到如果在一条不加密的网络上通信是无法保证信息的可靠传输的，在此基础上建立的应用也就没有可信之说。

为了解决上面的三个问题，我们就需要一套密码体系。

1.1 基本元素

通常一个密码体系由一个五元组组成，这个五元组的构成如下；

明文M：原始数据，待加密的数据；
密文C：对明文M进行一定变换或伪装后的输出；
密钥K：加密或解密中所使用的专门工具；
加密E：将明文M，通过密钥K变换得到密文C的过程；
解密D：将密文还原成明文M的过程；

一个密码系统的构建就是基于这个五元组{ M，C，K，E，D }，无论是比特币，还是以太坊千亿美元市值的数字货币都是基于这个密码体系，甚至整个区块链系统都是基于这个密码体系展开。

需要特别注意的是并非所有的加密算法的安全性都可以从数学上得到证明，目前公认的高强度的加密算法和实现往往经过长时间各方面充分的实践和论证后，才被大家所认可，但是也绝非代表其不存在漏洞。因此自行设计和发明未经大规模验证的加密算法是一种不太明智的行为，即使不公开算法的加密过程，也很容易遭到破解，无法在安全性上得到保障。

实际上，密码学实现的安全往往是通过算法所依赖的数学问题来提供的，而非通过对算法实现的过程来进行保密的。

1.2 对称加密

对称加密是指进行明文到密文加密时采用的密钥和密文到明文解密时使的密钥是相同的。
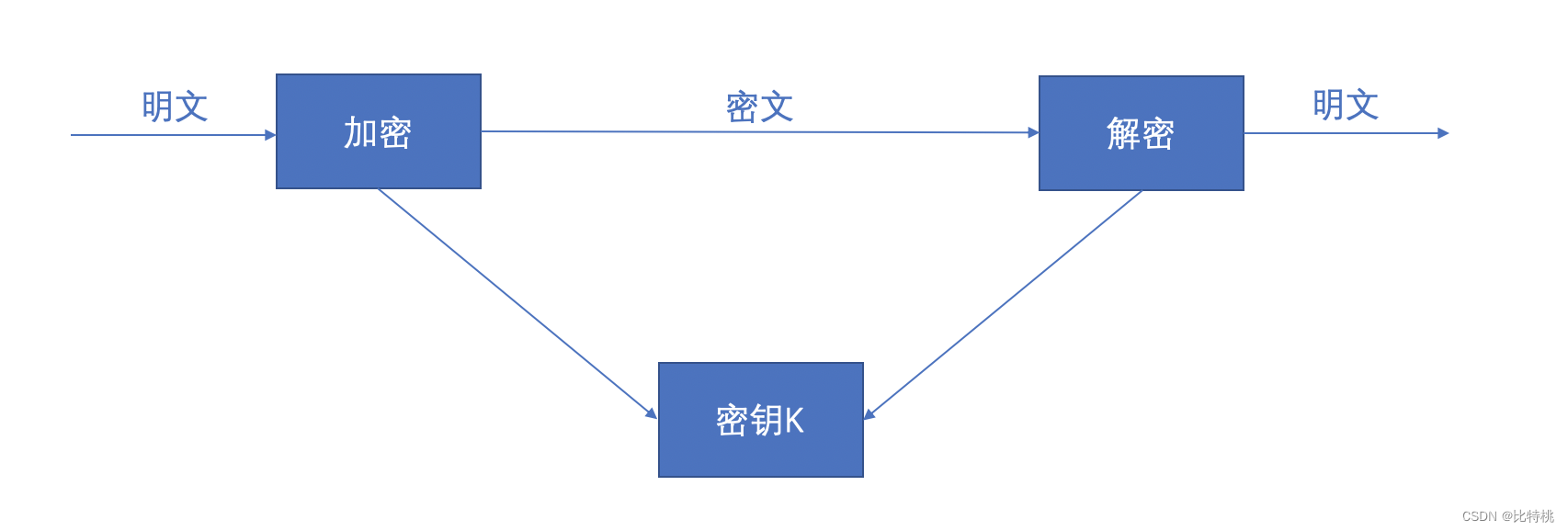
在这里插入图片描述
对称加密算法的优点是加密速度快，保密强度高，适用于对大量数据进行加密的过程。但是由于双方都使用相同的密钥K，密钥的传输和管理就是一个很大的问题，如果传输过程
不安全可靠，密钥就无法传递，只能通过其它方法传递，比如邮件，电话，短信等方式，可是这些通信方式是否可靠还待商榷。为了解决这个问题一般需要借助迪菲-赫尔曼秘钥交换（Elliptic Curve Diffie–Hellman key Exchange）协议来完成密钥分发。

由于每一对发送方和接收方都需要使用一个密钥，在区块链这种需要大规模通信的网络中会产生大量的密钥，也会增加用户管理密钥的负担。

代表算法：DES，AES；

1.3 非对称加密

非对称加密是指进行明文到密文加密和密文到明文解密时使用不同的密钥，非对称加密在使用前首先要生成公私钥对，一个用于加密，一个用于解密，其中用于加密的密钥可以公开，称之为公钥（Public Key），用于解密的密钥需要严格保存不能公开，称之为私钥（Private Key）。
在这里插入图片描述
非对称加密解决了对称密钥传输难的问题，降低了密钥管理的难度，通信双方不需要通过建立一个安全的信道来进行密钥的交换，但是又引入了新的问题。
非对称加密算法的加解密速度慢于对称加密，不适合大量数据的加解密，性能比较差，同时因为公钥公开，如果有人用公钥加密数据发送给我，是无法判断发送者是谁的；

代表算法：RSA，椭圆曲线算法;

1.4 混合加密

混合加密同时使用了对称加密和非对称加密方法，对称加密的一个很大问题是通信双方如何将密钥传输给对方，为了安全，一般采用带外传输，也就是说如果加密通信是在网络中，那么密钥的传输就需要通过其他途径，如邮件，短信，即使如此也很难保证密钥传输的安全性。非对称加解密的最大优点是事先不需要传输密钥，但是速度慢，因此实际应用中，通常采用混合密码体制。

1.5 消息摘要

消息摘要就是采用单向哈希（Hash）函数将需要加密的明文“提取摘要”生成一串固定长度的密文，这一串密文又称为数字指纹，它有固定的长度，而且不同的明文提取摘要生成的密文其结果总是不同的，但是同样的明文产生的摘要是一致的。由于生成摘要的明文是没有任何限制的，但是得到的摘要却是定长的，必然就会导致有一些明文会产生相同的摘要，这种现象被称为”碰撞“。为了避免这种情况的产生哈希函数必须具备很好的抗碰撞性，意味着在现有的计算资源（包括时间、空间、资金等）下，找到一个碰撞是不可行的。

摘要算法就是产生信息摘要算法，它有一个特性，就是在输入信息中如果发生细微的改变，比如给变了二进制的一位，都可以改变散列值中每个比特的特性，导致最后的输出结果大相径庭，所以它对于检测消息或者密钥等信息对象中的任何微小的变化非常有用。可以归纳出消息摘要如下的四个特点；

输入长度是任意的，输出是固定的；
对每一个给定的输入,计算输出是很容易的；
给定H,找到两个不同的输入，输出同一个值在计算上不可行；
给定H和一个消息x,找到另一个不同的消息y，使它们散列到同一个值在计算上不可行；

常见的散列算法：MD5、SHA、SHA-256、SHA-512；

在本文中，经常会看到SHA-256算法，这个也是在比特币，以太坊中大量使用的摘要算法，SHA-256算法对任意的输入产生定长的32byte，256位的输出，为了更方便的展示，一般都会采用Hex编码的方式来对结果进行编码。

以123为例，计算SHA-256后用Hex编码得到的结果是a665a45920422f9d417e4867efdc4fb8a04a1f3fff1fa07e998e86f7f7a27ae3。

哈希算法并不是一种加密算法，不能用于对信息的保护。但是哈希算法常用于对口令的保存上。例如用户登录网站需要通过用户名和密码来进行验证，如果网站后台直接保存了口令的明文，一旦发生了数据泄露后果就不堪设想。因为大多数用户都倾向于在多个网站使用相同的密码。利用哈希的特性，网站可以保存用户口令的哈希值，这样比较口令最终的哈希值即可，如果一致则证明口令是正确的。即使发生了数据泄露也很难根据单向哈希值推算出原始口令。

但是有时候由于用户口令的强度太低，只使用一些简单的字符串，比如123456等，攻击者可以通过对这些口令提前计算哈希，得到口令和哈希值的一种映射关系来达到破解的目的。为此了更多的提高安全性，网站一般会通过加盐（salt）的方式来计算哈希，不直接保存用户哈希而是通过口令加上一段随机字符（即“盐”）再计算哈希值，这样通过把哈希值和盐分开保存可以极大的提高安全性。

1.6 数字证书

数字证书是一种权威的电子证明，由权威公正的第三方认证机构（CA）签发，用来证明公开密钥拥有者的身份，其中包含了公钥信息、拥有者身份信息、以及数字证书认证机构（发行者）对这份文件的数字签名，以保证这个文件的整体内容正确无误，广泛用于涉及需要身份认证和数据安全的领域，简单来说就是证明这个公钥被谁拥有。

数字证书主要用来保证信息保密、身份确认、不可否认性、数据完整性，最为常见的格式是X.509。

1.7 数字签名

在现实世界中，文件上手书签名已经长期被用为原作者的证明，或用来表示同意文件所列的条款。签名不可辩驳的事实是：

签名是不可伪造的，签名是签名者慎重签在文件上的证明。
签名是可信的。签名使文件的接受者相信文件已由签名者慎重签名。
签名是不可再用的。签名是文件的一部分，不择手段的人不能把签名移到不同的文件上。
签名文件是不可能改变的。文件签名后，不能改变。
签名不能否认，签名和文件是一个物理事件，签名者以后不能宣布他或她没签名。

在实际上，上述叙述没有一个完全是真的。签名能被伪造，签名能从一张纸上剽窃来并移动另一处，签名后文件能坡改变。然而，因为欺骗的困难和俭测的出现，所以我们仍愿与这些问题一同生活。

要想在计算机上签名，有很多问题。首先，比特流容易拷贝。即使人的签名是难以伪造（例如手写，签名的图形图像），但把一个文件的有效签名移动到另一个文件中是容易的。这种签名毫无意义。第二，签名后，仍容易修改文件，并不留下任何修改的痕迹。

数字签名（英语：Digital Signature，又称公钥数字签名）是一种功能类似写在纸上的普通签名、但是使用了公钥加密领域的技术，以用于鉴别数字信息的方法。一套数字签名通常会定义两种互补的运算，一个用于签名，另一个用于验证。通常来说用私钥签名，签名后的消息表示签名人对该消息的内容负责，公钥用来验证签名的正确性。数字签名使用了消息摘要和非对称加密技术，可以保证接受者能够核实发送者对消息的签名，发送者事后不能抵赖对消息的签名，接受者不能篡改报文内容和伪造对报文的签名。

举一个例子说明下整个过程，假设Alice向Bob发送一条消息，Alice首先对消息生成了一个消息摘要，生成完成后对该消息用私钥进行签名附带在消息的最后，然后将消息和签名发送给了Bob，Bob收到消息后用同样的算法生成消息摘要，然后拿Alice的公钥验证这个消息摘要，验证通过则表明消息确实是Alice发来的。Alice的公钥可以放在网站上让大家获得，或者发邮件等方式告知大家。

通过数字签名可以确保两点；

确认信息是由签名者发送；
确认信息从签发到接受没有被修改过，包括传输中的中间人修改。

数字签名的过程：

发送方要发送消息运用散列函数（MD5、SHA-1等）形成消息摘要；
发送方用自己的私钥对消息摘要进行加密，形成数字签名；
发送方将数字签名附加在消息后发送给接收方；
接受方用发送方的公钥对签名信息进行解密，得到消息摘要；
接收方以相同的散列函数对接收到的消息进行散列，也得到一份消息摘要；
接收方比较两个消息摘要，如果完全一致，说明数据没有被篡改，签名真实有效；否则拒绝该签名。

1）多重签名
多重签名（Multi Signature）是数字签名的一个重要应用方式，通常用于多个参与者对某个消息，文件和资产同时拥有签名权或者支付权的场景。比如在生活中一份文件有时需要多个部门联合签字后方可生效。根据签名顺序的不同，又将多重签名分为了两类，有序多重签名和广播多重签名，对于第一种多重签名方式来说，签名者多次签名是有一定的串行顺序的，而第二种方式则没有限制。当数字资产需要经过多重签名确认后才能转移会极大的提高资产的安全性，恶意攻击者需要获得至少一个私钥才能盗用这些资产，同时也降低了用户无疑间泄露私钥所带来的风险和损失，因此多重签名在比特币脚本和以太坊智能合约中都有广泛的应用。

2）群签名

群签名（group signature）是由1991年，Chaum 和 Heyst首次提出群签名的概念，即某个群组内一个成员可以代表群组进行匿名的签名，签名可以证明来自于该群组，却无法确定来自于群组中的哪一个具体成员。群签名方案的关键是“群管理员”，它负责添加群成员，并能够在发生争议时揭示签名者身份。在一些群签名的设计方案中，添加成员和撤销签名匿名性的责任被分开，并分别赋予给群管理员和撤销管理员，但无论如何所有方案都应该满足基本的安全性要求。

3）环签名

环签名（ring signature）是由三位密码学家Ron Rivest，Adi Shamir和Yael Tauman在2001年首次提出的。在环签名中，签名者首先会选定一个临时的签名者集合，集合中包括签名者自身。然后签名者利用自己的私钥和集合中其他人的公钥就可以独立的产生签名，无需其他设置。签名者集合中的其他成员可能并不知道自己以及被包含在最终的集合签名集合中。环形签名的安全属性之一是，确定使用哪个组成员的密钥来生成签名应该在计算上不可行。环签名类似于组签名但在两个关键方面有所不同：第一，无法撤消单个签名的匿名性；第二，任何用户组都可以用作一个组。

4）盲签名

盲签名（blind signature）是在1982年由David Chaum提出的。签名者在无法看到原始内容的前提下对消息进行签名。盲签名可以实现对所签内容的保护，防止签名者看到原始的内容；另一方面盲签名还可以实现防止追踪，签名者无法将内容和签名结果进行对应。

二、BTC 的秘密

学习了上面这么多加密学的基础，终于来说到重点了。我们 BTC 其实主要用到了两个部分：

2.1 哈希

Hash（哈希）学过数据结构的同学应该了解Hash table，它其实就是将一个数据经过哈希运算后，可以得到一个的数值所映射代表。BTC 所使用的 Hash 算法 SHA-256（secure hash algorithm）满足了如下三个特性：

Collision resistance 哈希碰撞

即：X ≠ Y ，H(X) ≠ H(Y)
通过鸽笼原理我们知道，如果不同的内容可以得到相同的 Hash 结果，那么我们称这个 Hash 函数是不满足可碰撞的。
区块链的上的数据被哈希加密后就成为了 digest，用来防止被篡改。
有一些哈希函数是没有办法做到 Collision resistance 的，有些可以。e.g. MD5，已经被破解。

Hiding 不可逆

如果给定 Hash(X)、Hash()，无法反推出 X 则成为是不可逆的。通过这种不可逆的 Hash 函数，用来满足其数字的安全。
当然这也是一个很理想的情况，实际为了防止被人猜到，可以使用 H（X + nonce）

puzzle friendly 没有投机取巧可言

在比特币系统中，还需要第三个性质Puzzle friendly，工作即是最好的证明。该性质要求哈希值计算事先不可预测，仅仅根据输入很难预测出输出。
BTC 在开拓一个新的区块的时候会有一个 Target 值，而这个值会经过这样的运算：H（block header） ≤ target。也就是说谁能第一个算出来就可以拿到这个区块的 BTC 奖励，所以只能不断的去尝试也就是我们常听到的挖K。所谓的挖K就是去尝试组合各种不同的数去做 Hash 运算，得到的结果和H（block header）对比。如果不对继续变数算，如果对了就代表暴力破解出了 Target ，算是挖K成功。
我们需要一个哈希值，存在于某一个范围内，只能通过不停运算查找出来。该性质保证了比特币系统中，只能通过“挖K”获得比特币。也就是说，该性质保证了工作量证明(POW)机制。
如果你算出来了就可以告诉周围小伙伴了，因为是Hash运算，即：Difficult to solve, but easy to verify. 所以很快大家就承认你就是这个区块的主人，你可以得到这个奖励。

2.2 签名

在 BTC 的世界里，万物皆是一等公民。包括开账户本身，只需要一个公钥和私钥即可（非对称加密）。
用户在区块链上发布一个交易，用私钥签名，大家用公钥查看，判定是否是同一个人。
这种非对称加密算法满足：A good source of randomness，用来防止暴力破解。所以很难通过生成大量的公私钥对来获取他人私钥。