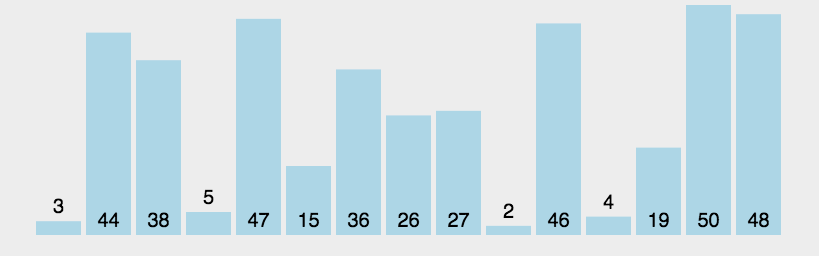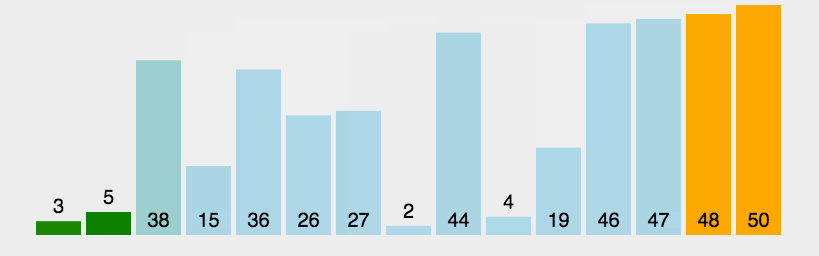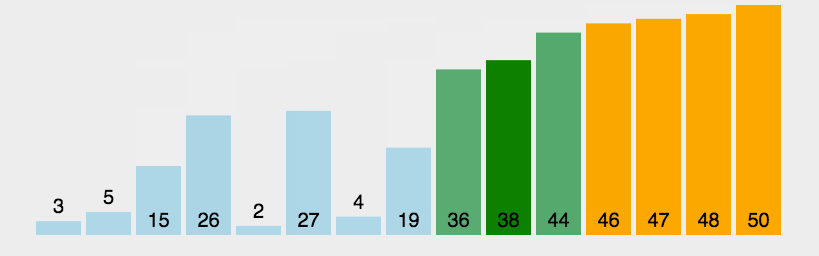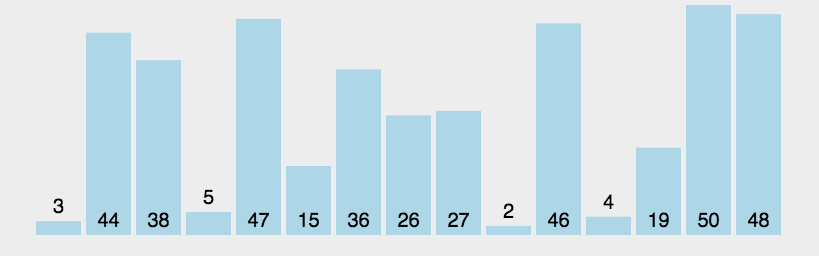435. 无重叠区间

题目链接🔥🔥
给定一个区间的集合，找到需要移除区间的最小数量，使剩余区间互不重叠。
注意: 可以认为区间的终点总是大于它的起点。 区间 [1,2] 和 [2,3] 的边界相互“接触”，但没有相互重叠。

示例 1:
输入: [ [1,2], [2,3], [3,4], [1,3] ]
输出: 1
解释: 移除 [1,3] 后，剩下的区间没有重叠。

示例 2:
输入: [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。

示例 3:
输入: [ [1,2], [2,3] ]
输出: 0
解释: 你不需要移除任何区间，因为它们已经是无重叠的了。

思路分析

感觉要排序，但是究竟是按照右边界排序，还是按照左边界排序呢？

其实都可以。主要就是为了让区间尽可能的重叠。

我来按照右边界排序，从左向右记录非交叉区间的个数。最后用区间总数减去非交叉区间的个数就是需要移除的区间个数了。

此时问题就是要求非交叉区间的最大个数。

这里记录非交叉区间的个数还是有技巧的，如图：

区间，1，2，3，4，5，6都按照右边界排好序。

当确定区间 1 和 区间2 重叠后，如何确定是否与 区间3 也重贴呢？

就是取 区间1 和 区间2 右边界的最小值，因为这个最小值之前的部分一定是 区间1 和区间2 的重合部分，如果这个最小值也触达到区间3，那么说明 区间 1，2，3都是重合的。

接下来就是找大于区间1结束位置的区间，是从区间4开始。那有同学问了为什么不从区间5开始？别忘了已经是按照右边界排序的了。

区间4结束之后，再找到区间6，所以一共记录非交叉区间的个数是三个。

总共区间个数为6，减去非交叉区间的个数3。移除区间的最小数量就是3。

C++代码如下：

class Solution {
public:
    // 按照区间右边界排序
    static bool cmp (const vector<int>& a, const vector<int>& b) {
        return a[1] < b[1];
    }
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        if (intervals.size() == 0) return 0;
        sort(intervals.begin(), intervals.end(), cmp);
        int count = 1; // 记录非交叉区间的个数
        int end = intervals[0][1]; // 记录区间分割点
        for (int i = 1; i < intervals.size(); i++) {
            if (end <= intervals[i][0]) {
                end = intervals[i][1];
                count++;
            }
        }
        return intervals.size() - count;
    }
};

左边界排序可不可以呢？

也是可以的，只不过 左边界排序我们就是直接求 重叠的区间，count为记录重叠区间数。

class Solution {
public:
    static bool cmp (const vector<int>& a, const vector<int>& b) {
        return a[0] < b[0]; // 改为左边界排序
    }
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        if (intervals.size() == 0) return 0;
        sort(intervals.begin(), intervals.end(), cmp);
        int count = 0; // 注意这里从0开始，因为是记录重叠区间
        int end = intervals[0][1]; // 记录区间分割点
        for (int i = 1; i < intervals.size(); i++) {   
            if (intervals[i][0] >= end)  end = intervals[i][1]; // 无重叠的情况
            else { // 重叠情况 
                end = min(end, intervals[i][1]);
                count++;
            }
        }
        return count;
    }
};

我的：

class Solution {
public:
    static bool compare(vector<int>& a,vector<int>& b){
        return a[0]<b[0];
    }
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        int result=0;
        sort(intervals.begin(),intervals.end(),compare);
        for(int i=1;i<intervals.size();i++){
            if(intervals[i][0]<intervals[i-1][1]){
                result++;
                intervals[i][1]=min(intervals[i][1],intervals[i-1][1]);
            }
        }
        return result;
    }
};

---

763.划分字母区间

题目链接🔥🔥
字符串 S 由小写字母组成。我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。返回一个表示每个字符串片段的长度的列表。

示例：
输入：S = “ababcbacadefegdehijhklij”
输出：[9,7,8] 解释： 划分结果为 “ababcbaca”, “defegde”, “hijhklij”。 每个字母最多出现在一个片段中。 像 “ababcbacadefegde”, “hijhklij” 的划分是错误的，因为划分的片段数较少。

提示：
S的长度在[1, 500]之间。
S只包含小写字母 ‘a’ 到 ‘z’

思路分析

题目要求同一字母最多出现在一个片段中，那么如何把同一个字母的都圈在同一个区间里呢？

如果没有接触过这种题目的话，还挺有难度的。

在遍历的过程中相当于是要找每一个字母的边界，如果找到之前遍历过的所有字母的最远边界，说明这个边界就是分割点了。此时前面出现过所有字母，最远也就到这个边界了。

可以分为如下两步：

• 统计每一个字符最后出现的位置
• 从头遍历字符，并更新字符的最远出现下标，如果找到字符最远出现位置下标和当前下标相等了，则找到了分割点

如图：

代码实现

我的：

class Solution {
public:
    vector<int> partitionLabels(string s) {
        vector<int> result;
        vector<int> record(26,0);
        for(int i=0;i<s.size();i++){// 统计每一个字符最后出现的位置
            record[s[i]-'a']=i;
        }
        int left=0;
        int right=0;
        for(int i=0;i<s.size();i++){
            right=max(right,record[s[i]-'a']);// 找到字符出现的最远边界
            if(i==right) {
                result.push_back(right-left+1);
                left=right+1;
            }
        }
        return result;
    }
};

思考总结

就是用最远出现距离模拟了圈字符的行为

---

56. 合并区间

题目链接🔥🔥
给出一个区间的集合，请合并所有重叠的区间。

示例 1:
输入: intervals = [[1,3],[2,6],[8,10],[15,18]]
输出: [[1,6],[8,10],[15,18]]
解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

示例 2:
输入: intervals = [[1,4],[4,5]]
输出: [[1,5]]
解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。
注意：输入类型已于2019年4月15日更改。 请重置默认代码定义以获取新方法签名。

思路分析

都是判断区间重叠，区别就是判断区间重叠后的逻辑，本题是判断区间重贴后要进行区间合并。

所以一样的套路，先排序，让所有的相邻区间尽可能的重叠在一起，按左边界，或者右边界排序都可以，处理逻辑稍有不同。

按照左边界从小到大排序之后，如果 intervals[i][0] <= intervals[i - 1][1] 即intervals[i]的左边界 <= intervals[i - 1]的右边界，则一定有重叠。（本题相邻区间也算重贴，所以是<=）

这么说有点抽象，看图：（注意图中区间都是按照左边界排序之后了）

知道如何判断重复之后，剩下的就是合并了，如何去模拟合并区间呢？

其实就是用合并区间后左边界和右边界，作为一个新的区间，加入到result数组里就可以了。如果没有合并就把原区间加入到result数组。

标答：

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        vector<vector<int>> result;
        if (intervals.size() == 0) return result; // 区间集合为空直接返回
        // 排序的参数使用了lambda表达式
        sort(intervals.begin(), intervals.end(), [](const vector<int>& a, const vector<int>& b){return a[0] < b[0];});

        // 第一个区间就可以放进结果集里，后面如果重叠，在result上直接合并
        result.push_back(intervals[0]); 

        for (int i = 1; i < intervals.size(); i++) {
            if (result.back()[1] >= intervals[i][0]) { // 发现重叠区间
                // 合并区间，只更新右边界就好，因为result.back()的左边界一定是最小值，因为我们按照左边界排序的
                result.back()[1] = max(result.back()[1], intervals[i][1]); 
            } else {
                result.push_back(intervals[i]); // 区间不重叠 
            }
        }
        return result;
    }
};

class Solution {
public:
    static bool compare(vector<int>& a,vector<int>& b){
        return a[0]<b[0];
    }
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        vector<vector<int>> result;
        sort(intervals.begin(),intervals.end(),compare);
        for(int i=1;i<intervals.size();i++){
            if(intervals[i][0]<=intervals[i-1][1]){
                intervals[i][0]=min(intervals[i][0],intervals[i-1][0]);
                intervals[i][1]=max(intervals[i][1],intervals[i-1][1]);
            }
            else result.push_back(intervals[i-1]);
        }
        result.push_back(intervals[intervals.size()-1]);
        return result;
    }
};

---