课程链接三维视觉

作业任务任务

课程任务就一个，实现一个Linear Sweep Algorithm，这个算法是用来检测两张图片之间的对应点。

因为SIFT检测如果把检测点的数量增大，可能会存在一些错误错误检测点，所有通常把SIFT检测的点的数量k设置为很小，这样虽然减少了出错率，但是检测的点少了。所有我们需要使用linear sweep算法补充这些点。

实现

他给出的实现已经写的很清楚了。

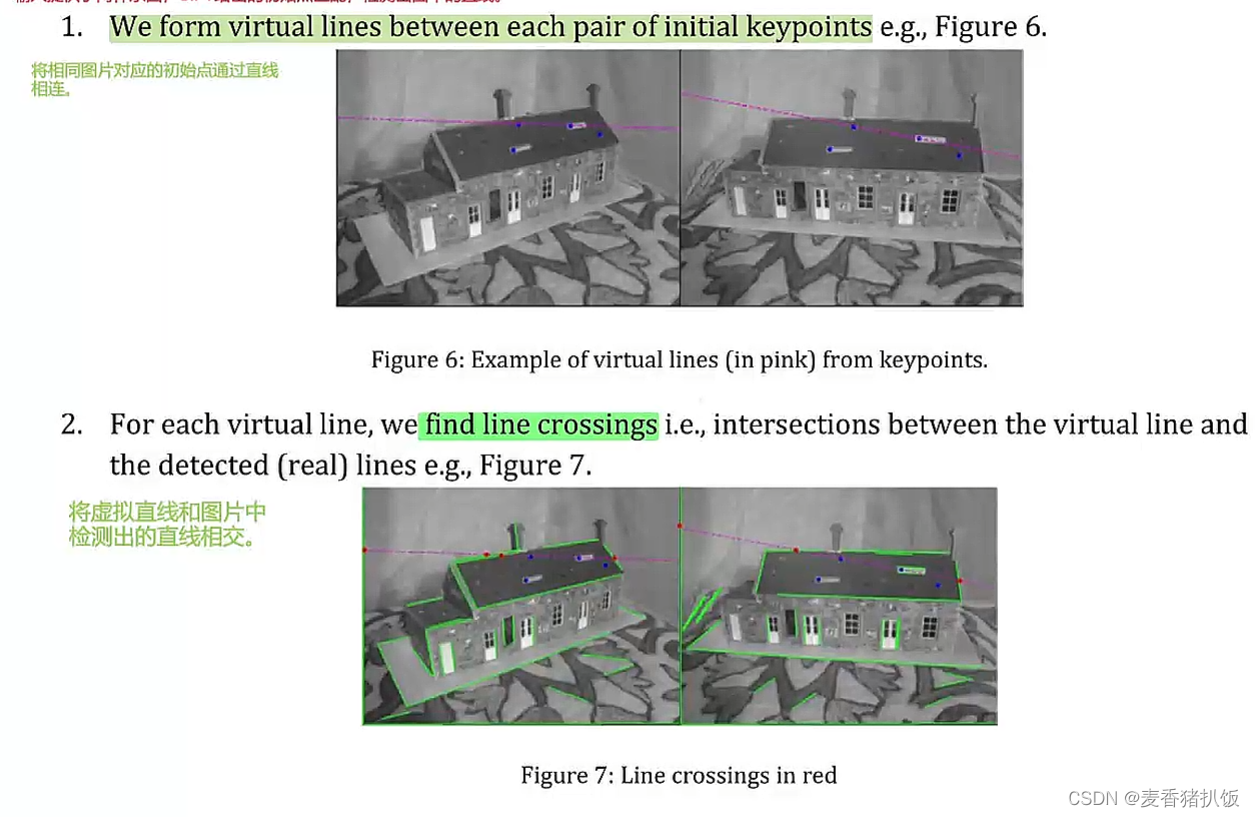
需要实现五个方法：

1. get_keypoints
2. get_matches
3. convert_line_pts_to_lines
4. get_line_intersections
5. get_line_crossings
6. get_cross_ratios

都比较简单，convert_line_pts_to_lines是两种直线不同表示方法之间的转换，原本的表示是起点和终点，两点确定一条直线，通过这个函数变成直线的标准形式(a, b, 1)，也即是ax+by+1 = 0。其中l = (a, b, 1)需要满足$l{x}^T=0,l{y}^T=0$。所有直接算叉乘就行了。

    # 直接求叉乘就完事了，因为X * (X x Y) = 0, Y * (X X Y) = 0, 说明XY都在(X x Y)上了。
    lines = np.cross(pts, other_pts, axis=1)
    # 最后一项归一化成1
    lines = lines / (lines[:, -1].reshape(lines.shape[0], 1))

get_line_intersections算直线的交点，也是算叉乘就行：

    intersections = np.cross(lines, other_lines)
    intersections = intersections / (intersections[:, -1].reshape(intersections.shape[0], 1))

get_line_crossings算当前直线和检测直接的交点，这里麻烦一点，因为我们还需要确认交点是不是在起点和终点的范围内，所有求出交点后还需要对交点进行过滤。这里的过滤方法是：如果$P$是在$P_0$和$P_1$方法之间，那么就有$0<P_{0}P\ast P_0{P}_1<=|P_0{P}_1{|}^2$，因为$P$在$P_0{P}_1$上的的投影肯定在$P_0{P}_1$上。

    # 保证get_line_intersections的输入
    v_lines = np.ones_like(r_lines)
    v_lines[:, ] = v_line
    # 计算交点
    line_intersections = get_line_intersections(v_lines, r_lines)
    # 判断是否是在线段中间
    # P如果在P0和P1的中间，那么把PP0投影到P0P1一定会在0到|P0P1|上，所有有0 < P0P * P0P1 < |P0P1|^2
    for i, point in enumerate(line_intersections):
        prod = (point[0] - r_start_pts[i][0]) * (r_end_pts[i][0] - r_start_pts[i][0]) + \
            (point[1] - r_start_pts[i][1]) * (r_end_pts[i][1] - r_start_pts[i][1])
        sqrlen = (r_end_pts[i][0] - r_start_pts[i][0]) * (r_end_pts[i][0] - r_start_pts[i][0]) + \
            (r_end_pts[i][1] - r_start_pts[i][1]) * \        
            (r_end_pts[i][1] - r_start_pts[i][1])      
        if (prod >= 0 and prod <= sqrlen):
            line_crossings = np.concatenate((line_crossings, point))
    line_crossings = line_crossings.reshape(-1, 3)