✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab仿真内容点击👇

智能优化算法  神经网络预测 雷达通信  无线传感器

信号处理 图像处理 路径规划 元胞自动机 无人机  电力系统

⛄ 内容介绍

1 深度极限学习机

人工神经网络的最大缺点是训练时间太长从而限制其实时应用范围,近年来,极限学习机(Extreme Learning Machine, ELM)的提出使得前馈神经网络的训练时间大大缩短,然而当原始数据混杂入大量噪声变量时,或者当输入数据维度非常高时,极限学习机算法的综合性能会受到很大的影响。深度学习算法的核心是特征映射,它能够摒除原始数据中的噪声,并且当向低维度空间进行映射时,能够很好的起到对数据降维的作用,因此我们思考利用深度学习的优势特性来弥补极限学习机的弱势特性从而改善极限学习机的性能。在本文中,首先介绍了基于自编码器的极限学习机(Auto Encode based Extreme Learning Machine, AE-ELM),它使用第一层自编码网络对输入数据进行降维除噪处理,再使用第二层自编码算法确定ELM输入权值以提升ELM有效性,最后使用最小二乘法确定ELM输出层权值。这种方法主要解决数据维度偏高且含有噪声时的情况,最后实验验证了AE-ELM在噪声数据下很好的提升了算法的性能。其次,详细介绍了基于极限学习机的自编码器(Extreme Learning Machine Auto Encode, ELM-AE),它能够对原始特征进行等维度,高维度,及低维度的特征映射,为ELM在超高维度下的应用奠定了基础。

⛄ 部分代码

function X = pinv(A,tol)

%PINV   Pseudoinverse.

%   X = PINV(A) produces a matrix X of the same dimensions

%   as A' so that A*X*A = A, X*A*X = X and A*X and X*A

%   are Hermitian. The computation is based on SVD(A) and any

%   singular values less than a tolerance are treated as zero.

%

%   PINV(A,TOL) treats all singular values of A that are less than TOL as

%   zero. By default, TOL = max(size(A)) * eps(norm(A)).

%

%   Class support for input A: 

%      float: double, single

%

%   See also RANK.

%   Copyright 1984-2015 The MathWorks, Inc. 

A(isnan(A)) = 0;

A(isinf(A)) = 0;

[U,S,V] = svd(A,'econ');

s = diag(S);

if nargin < 2 

    tol = max(size(A)) * eps(norm(s,inf));

end

r1 = sum(s > tol)+1;

V(:,r1:end) = [];

U(:,r1:end) = [];

s(r1:end) = [];

s = 1./s(:);

X = (V.*s.')*U';

⛄ 运行结果

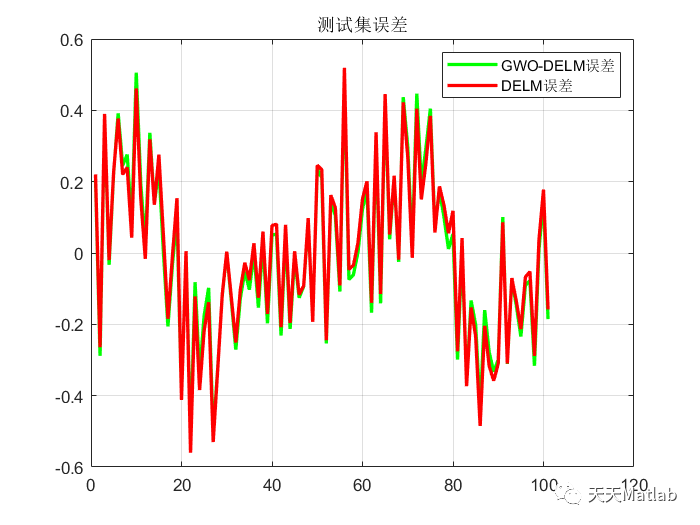
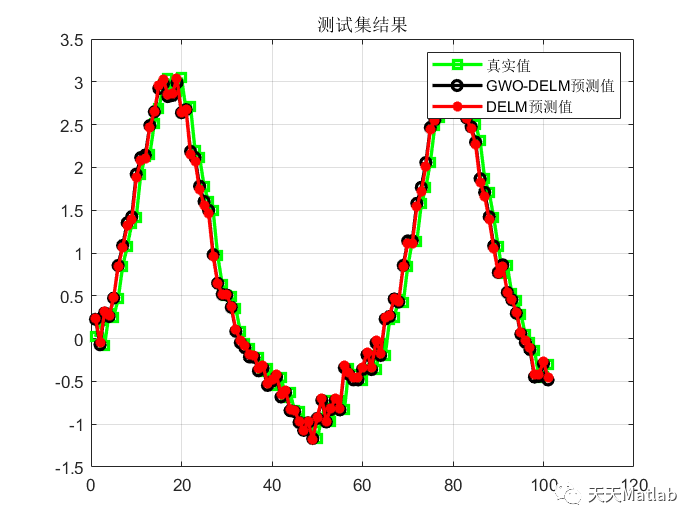
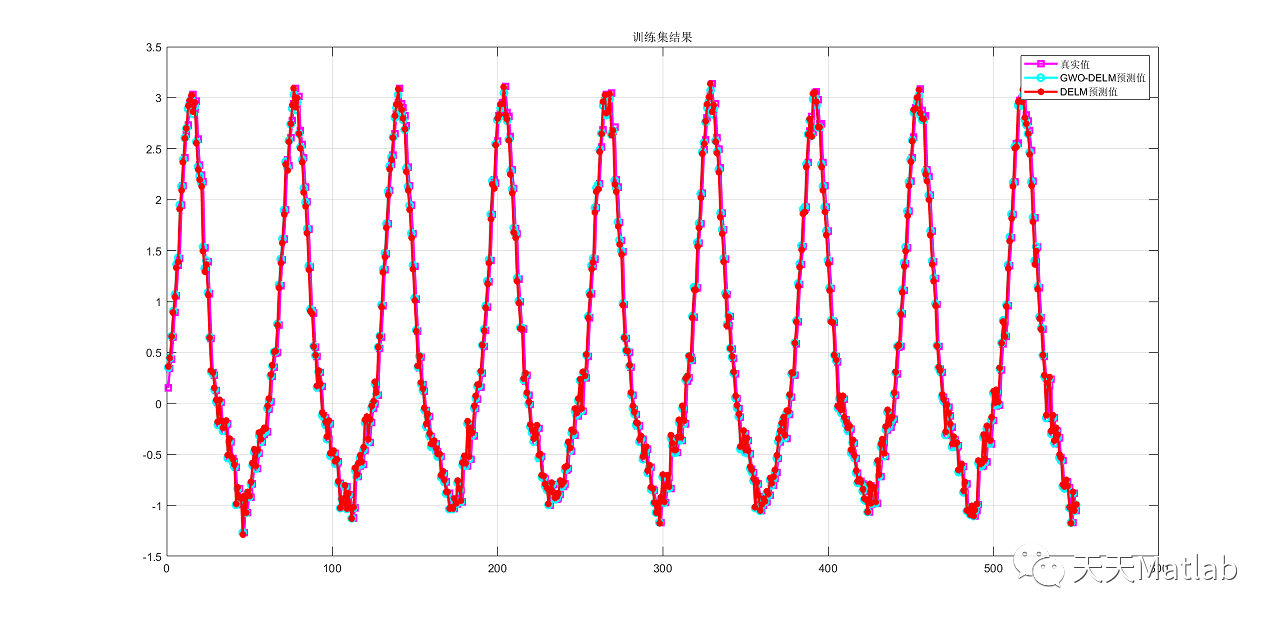
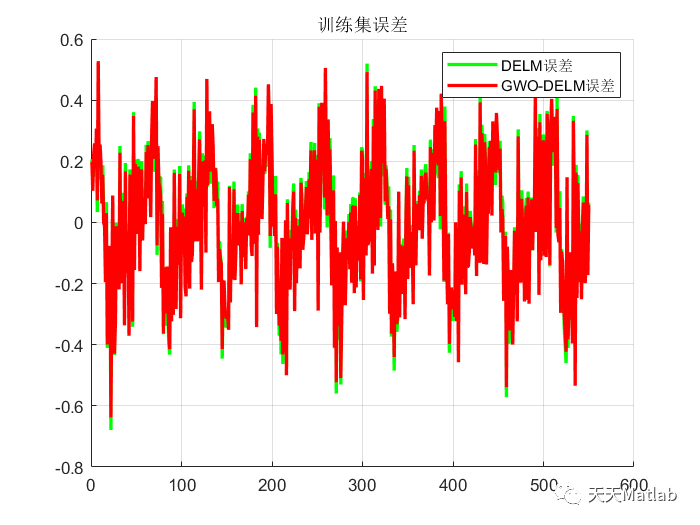
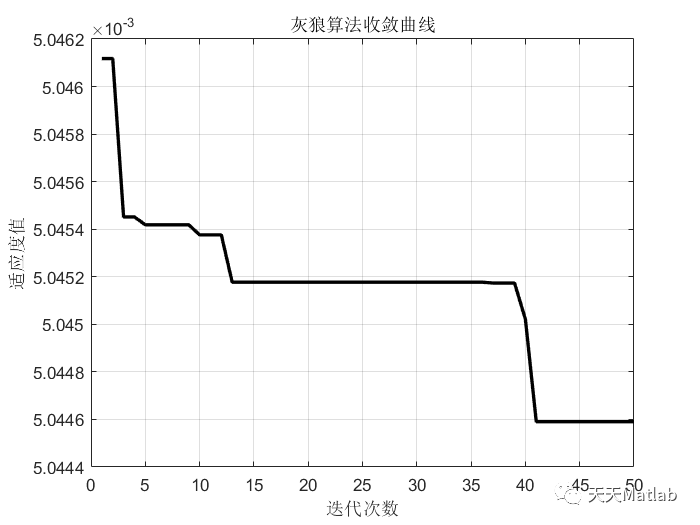
⛄ 参考文献

[1]杜柳青李仁杰李宝钏. 基于注意力机制的数控机床热误差深度学习预测方法[J]. 四川大学学报（工程科学版）, 2021, 053(006):194-203.

⛄ Matlab代码关注

❤️部分理论引用网络文献，若有侵权联系博主删除

❤️ 关注我领取海量matlab电子书和数学建模资料