本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库：https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

给你无向 连通 图中一个节点的引用，请你返回该图的 深拷贝（克隆）。

图中的每个节点都包含它的值 val（int） 和其邻居的列表（list[Node]）。

class Node {
    public int val;
    public List<Node> neighbors;
}

测试用例格式：
简单起见，每个节点的值都和它的索引相同。例如，第一个节点值为 1（val = 1），第二个节点值为 2（val = 2），以此类推。该图在测试用例中使用邻接列表表示。

邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。

给定节点将始终是图中的第一个节点（值为 1）。你必须将 给定节点的拷贝 作为对克隆图的引用返回。

示例 1：

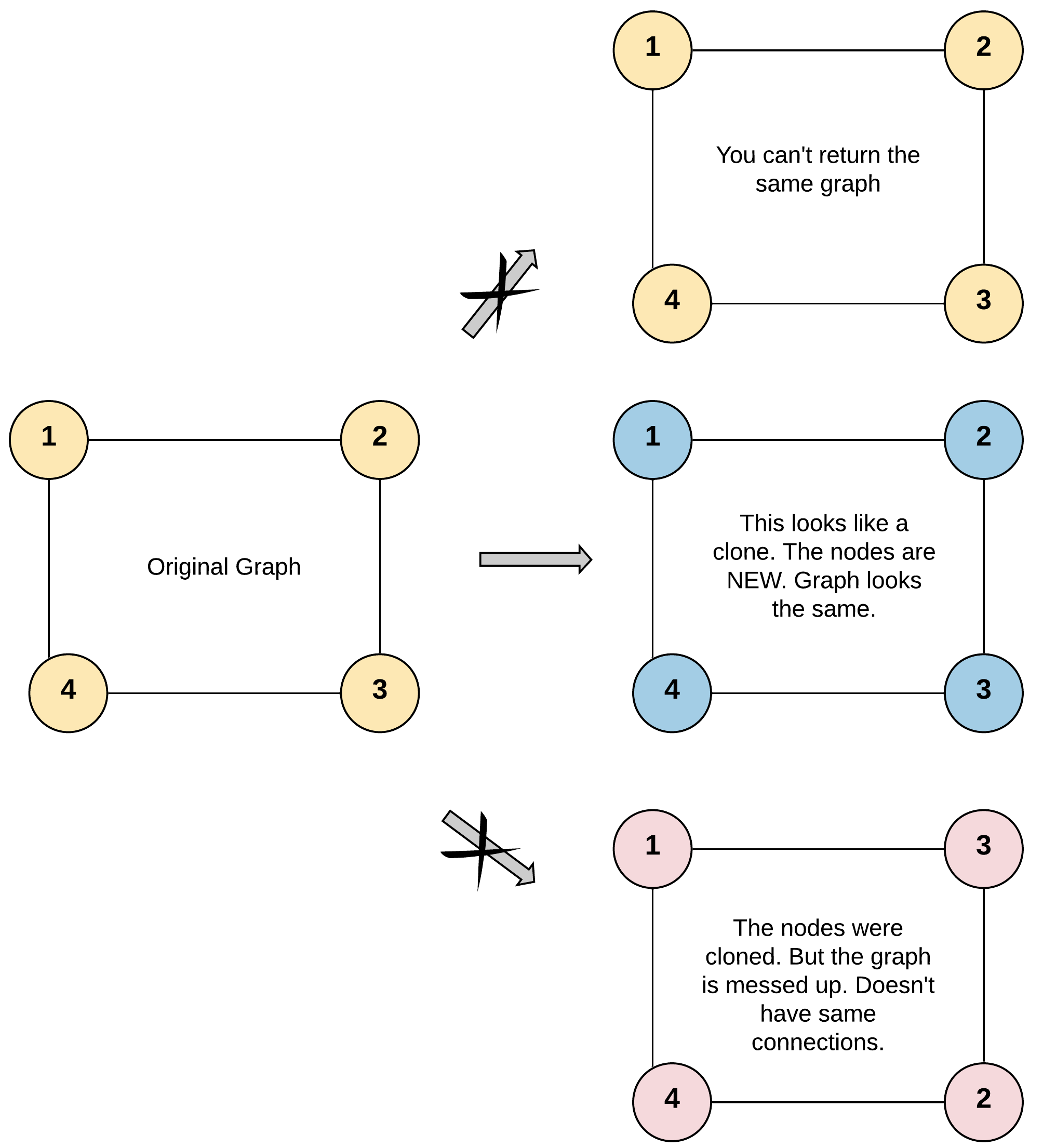
输入：adjList = [[2,4],[1,3],[2,4],[1,3]]
输出：[[2,4],[1,3],[2,4],[1,3]]
解释：
图中有 4 个节点。
节点 1 的值是 1，它有两个邻居：节点 2 和 4 。
节点 2 的值是 2，它有两个邻居：节点 1 和 3 。
节点 3 的值是 3，它有两个邻居：节点 2 和 4 。
节点 4 的值是 4，它有两个邻居：节点 1 和 3 。

示例 2：

输入：adjList = [[]]
输出：[[]]
解释：输入包含一个空列表。该图仅仅只有一个值为 1 的节点，它没有任何邻居。

示例 3：

输入：adjList = []
输出：[]
解释：这个图是空的，它不含任何节点。

示例 4：

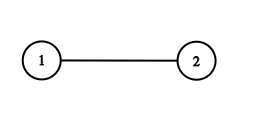
输入：adjList = [[2],[1]]
输出：[[2],[1]]

提示：

1. 节点数不超过 100 。
2. 每个节点值 Node.val 都是唯一的，1 <= Node.val <= 100。
3. 无向图是一个简单图，这意味着图中没有重复的边，也没有自环。
4. 由于图是无向的，如果节点 p 是节点 q 的邻居，那么节点 q 也必须是节点 p 的邻居。
5. 图是连通图，你可以从给定节点访问到所有节点。

---

对于本题而言，我们要明确图的深拷贝是在做什么，对于一张图而言，它的深拷贝即构建一张与原图结构、值均一样的图，但是其中的节点不再是原来图节点的引用。因此，为了深拷贝出整张图，我们需要知道整张图的结构以及对应节点的值。

由于题目只给了我们一个节点的引用，因此为了知道整张图的结构及对应节点的值，要从给定的节点出发，进行「图的遍历」，并在遍历的过程中完成图的深拷贝。

为了避免在深拷贝时陷入死循环，要理解图的结构。对于一张无向图，任何给定的无向边都可以表示为两个有向边，即如果节点 $A$ 和节点 $B$ 之间存在无向边，则表示该图具有从节点 $A$ 到节点 $B$ 的有向边和从节点 $B$ 到节点 $A$ 的有向边。

为了防止多次遍历同一个节点，陷入死循环；为了在设置 $neighbors$ 邻接点时，将克隆图中点 $A^{\prime }$ 的邻接点 $B^{\prime }$ 设置为「原图中 $A$ 的邻接点 $B$ 在克隆图中的复制节点 $B^{\prime }$ 」，我们需要用一种数据结构记录已经被克隆过的节点——用一个哈希表存储所有已被访问和克隆的节点。哈希表中的 $key$ 是原始图中的节点，$value$ 是克隆图中的对应节点。从给定节点开始遍历图。如果某个节点已经被访问过，则返回其克隆图中的对应节点。

解法1 DFS+哈希表

如下图，我们给定无向边边 $A-B$ ，表示 $A$ 能连接到 $B$ ，且 $B$ 能连接到 $A$ 。如果不对访问过的节点做标记，则会陷入死循环中。

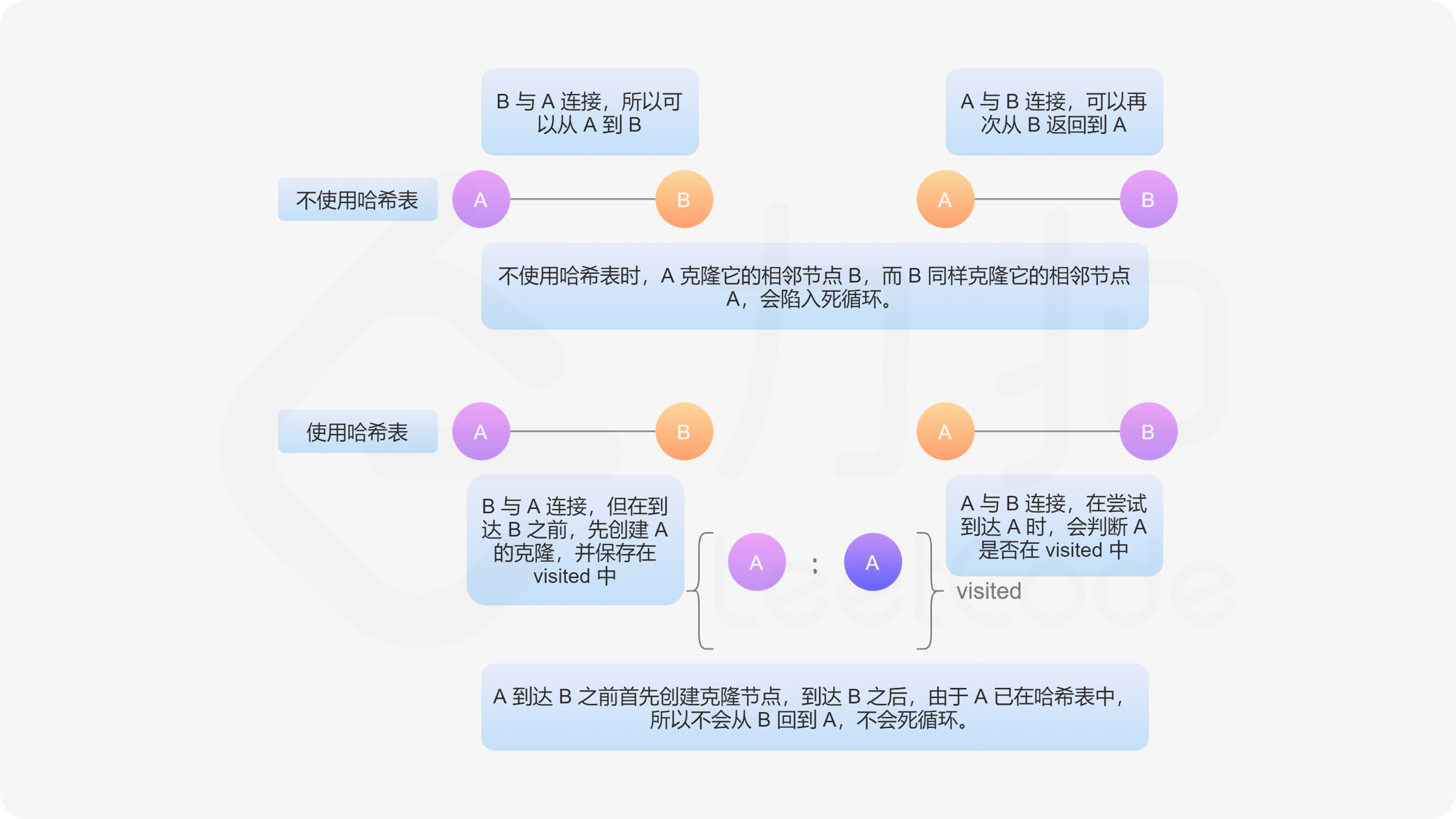
• 如果当前访问的节点不在哈希表中，则创建它的克隆节点并存储在哈希表中；否则直接返回哈希表中的克隆节点。注意：在进入递归之前，必须先创建克隆节点并保存在哈希表中。如果不保证这种顺序，可能会在递归中再次遇到同一个节点，再次遍历该节点时，陷入死循环。
  
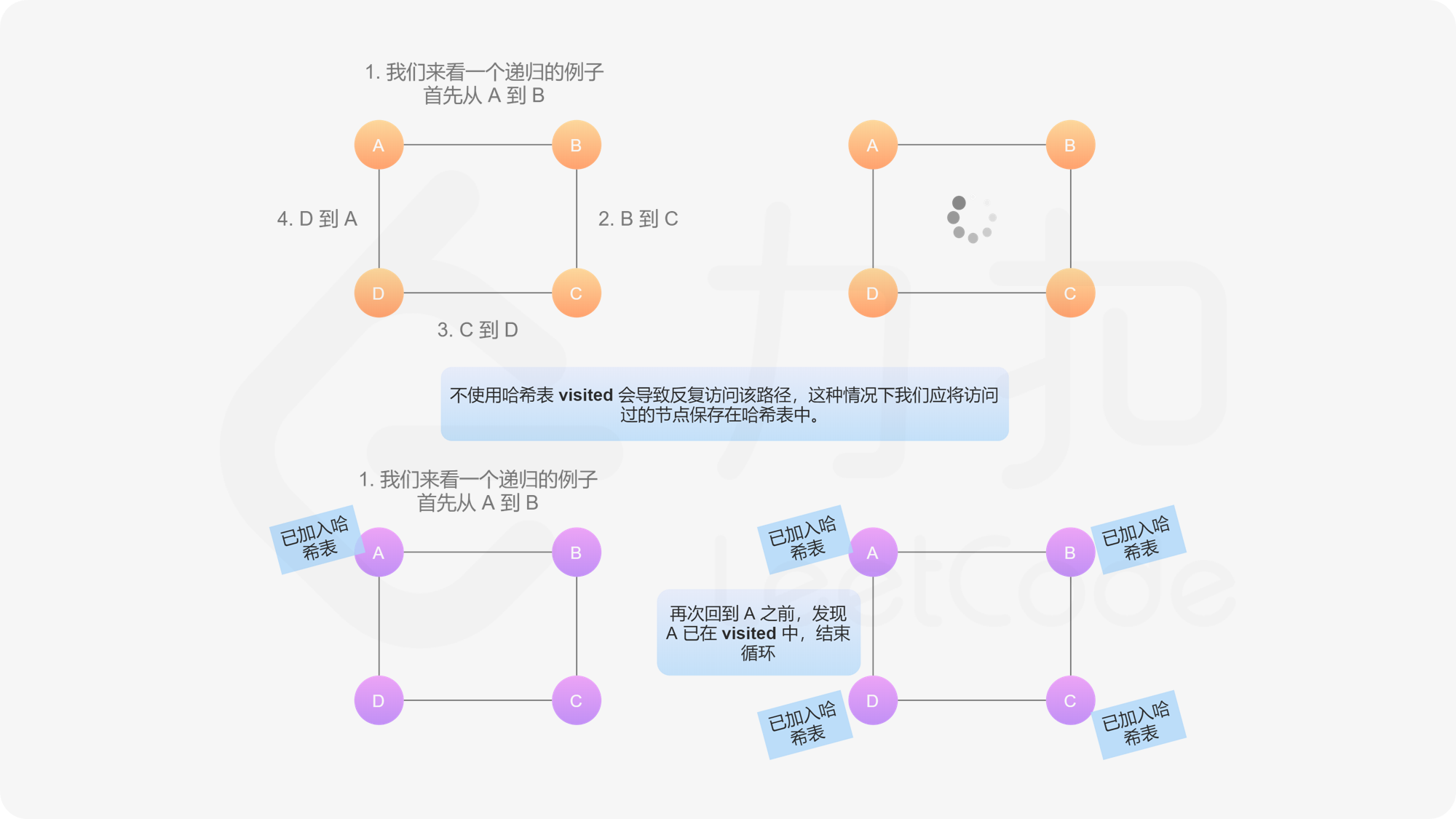
• 递归调用每个节点的邻接点。每个节点递归调用的次数等于邻接点的数量，每一次调用返回其对应邻接点的克隆节点，将其放入当前克隆节点的邻接表中。这样就可以克隆给定的节点和其邻接点。

class Solution {
public:
    unordered_map<Node*, Node*> vis;
    Node* cloneGraph(Node* node) {
        if (node == nullptr) return node;
        // 如果该节点已经被访问过了，则直接从哈希表中取出对应的克隆节点返回
        if (vis.find(node) != vis.end()) return vis[node];
        // 克隆节点，注意为了深拷贝我们不会克隆它的邻居的列表
        Node* cloneNode = new Node(node->val);
        // 哈希表存储
        vis[node] = cloneNode;
        // 遍历该节点的邻居并更新克隆节点的邻居列表
        for (Node *neighbor : node->neighbors)
            cloneNode->neighbors.emplace_back(cloneGraph(neighbor));
        return cloneNode;
    }
};

复杂度分析：

• 时间复杂度：$O(n)$ ，其中 $n$ 表示节点数量。深度优先搜索遍历图的过程中每个节点只会被访问一次。
• 空间复杂度：$O(n)$ 。存储克隆节点和原节点的哈希表需要 $O(n)$ 的空间，递归调用栈需要 $O(h)$ 的空间，其中 $h$ 是图的深度，经过放缩可以得到 $O(h)=O(n)$ ，因此总体空间复杂度为 $O(n)$ 。

---

解法2 BFS+哈希表

同样，我们也可以用广度优先搜索来进行「图的遍历」。方法一与方法二的区别仅在于搜索的方式。深度优先搜索以深度优先，广度优先搜索以广度优先。这两种方法都需要借助哈希表记录被克隆过的节点来避免陷入死循环。

1. 使用一个哈希表 $vis$ 存储所有已被访问和克隆的节点。哈希表中的 $key$ 是原始图中的节点，$value$ 是克隆图中的对应节点。
2. 将题目给定的节点添加到队列。克隆该节点并存储到哈希表中。
3. 每次从队列首部取出一个节点，遍历该节点的所有邻接点。
   1. 如果某个邻接点已被访问，则该邻接点一定在 $vis$ 中，那么从 $vis$ 获得该邻接点;
   2. 否则创建一个新的节点存储在 $vis$ 中，并将邻接点添加到队列。
   3. 将克隆的邻接点添加到克隆图对应节点的邻接表中。
4. 重复上述操作直到队列为空，则整个图遍历结束。

class Solution {
public:
    Node* cloneGraph(Node* node) {
        if (node == nullptr) return nullptr;
        unordered_map<Node*, Node*> vis;
        // 将题目给定的节点添加到队列
        queue<Node*> q;
        q.push(node);
        // 克隆第一个节点并存储到哈希表中
        vis[node] = new Node(node->val);
        
        while (!q.empty()) {
            // 取出队列头节点
            Node *cur = q.front(); q.pop();                
            for (auto& neighbor: cur->neighbors) {
                if (vis.find(neighbor) == vis.end()) {
                    // 如果没有被访问过，就克隆并存储在哈希表中
                    vis[neighbor] = new Node(neighbor->val);
                    q.push(neighbor);
                }
                // 更新当前节点的邻居列表
                vis[cur]->neighbors.emplace_back( vis[neighbor] );
            }
        }
        return vis[node];
    }
};

复杂度分析：

• 时间复杂度：$O(n)$ ，其中 $n$ 表示节点数量。广度优先搜索遍历图的过程中每个节点只会被访问一次。
• 空间复杂度：$O(n)$ 。哈希表使用 $O(n)$ 的空间。广度优先搜索中的队列在最坏情况下会达到 $O(n)$ 的空间复杂度，因此总体空间复杂度为 $O(n)$。