【数据结构】堆（一）——堆的实现

news2024/11/15 9:13:11

作者：一个喜欢猫咪的的程序员 

专栏：《数据结构》

喜欢的话：世间因为少年的挺身而出，而更加瑰丽。                                  ——《人民日报》

目录

堆的概念及结构：

堆的实现思路：（我们以大堆为例）

需要实现的接口：

 实现的一些细节：

HeapPush函数：

Ajustup函数：

HeapPop函数：

Ajustdown函数： 

代码实现：

Heap.h文件：

Heap.c文件:

Test.c文件：

堆的概念及结构：

如果有一个关键码的集合K = { ， ， ，…， }，把它的所有元素按完全二叉树的顺序存储方式存储
在一个一维数组中，并满足： <= 且 <= ( >= 且 >= ) i = 0，1，2…，则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

  • 父节点都比其的子节点大的完全二叉树叫做大堆。
  • 父节点都比其的子节点小的完全二叉树叫做小堆。

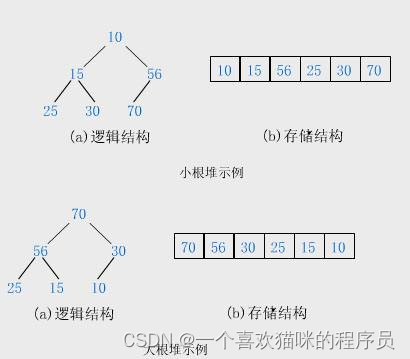
 堆的性质：

  • 堆中某个节点的值总是不大于或不小于其父节点的值；
  • 堆总是一棵完全二叉树。

堆的实现思路：（我们以大堆为例）

需要实现的接口：

void Swap(HPDataType* p1, HPDataType* p2);
void HeapCreate(HP* php, HPDataType* a, int n);
void HeapPrintf(HP* php);
void HeapInit(HP* php);
void HeapDestroy(HP* php);
void HeapPush(HP* php, HPDataType x);
void HeapPop(HP* php);
HPDataType HeapTop(HP* php);
int HeapSize(HP* hp);
bool HeapEmpty(HP* hp);
void Ajustdown(HPDataType* a, int n, int parent); 
void Ajustup(HPDataType* a, int n);

从堆的结构中，我们了解到堆是一个数组a，并且后续我们可能需要对数组进行扩容和缩小，因此我们还需要两个变量：有效长度size和容量capacity

 

 实现的一些细节：

 HeapInit、HeapDestroy、HeapPrintf函数没有什么好说的。

void HeapInit(HP* php)
{
	assert(php);
	php->capacity = 0;
	php->size = 0;
	php->a = NULL;
}
void HeapDestroy(HP* php)
{
	assert(php);
	assert(php->a);
	free(php->a);
	free(php);
}
void HeapPrintf(HP* php)
{
	assert(php);
	for (int i = 0; i < php->size; i++)
	{
		printf("%d ", php->a[i]);
	}
	printf("\n");
}

HeapPush函数：

因为我们的存储结构是一个数组，Push就直接添加数据吗？

当capacity==size时扩容一下（包括初始化的方案），当size==0时，扩容4个空间，否则扩容二倍的空间，capacity也跟着扩大，当push后size++。

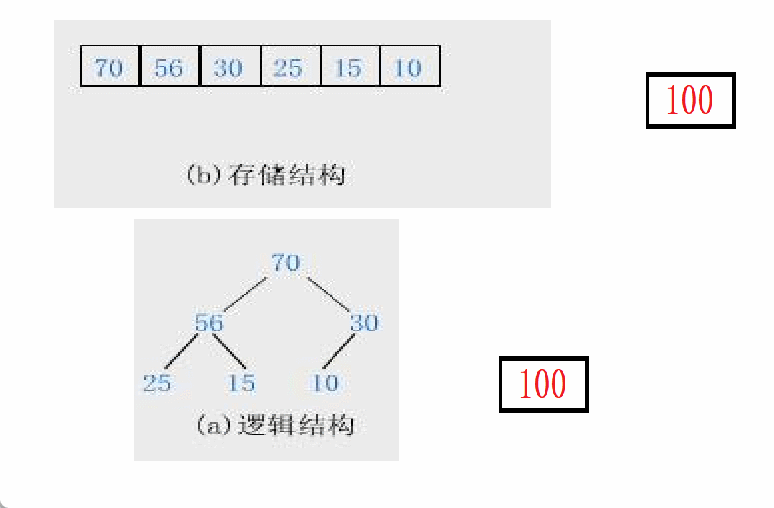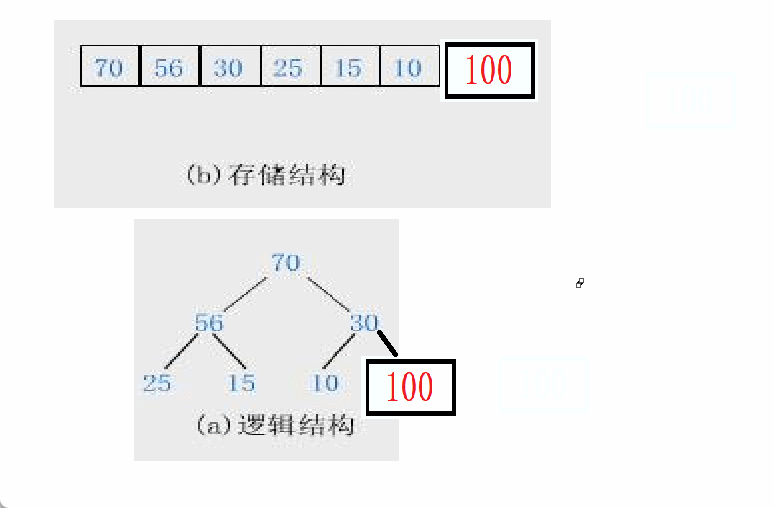
 以大堆为例：

100比30大，30和100需要调换位置，然后100又比70大，70和100需要再次调换位置。

我们添加的数据x作为子节点child，child可能会比它的父节点parent大。因此需要将child向上调整Ajustup。

void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	if (php->size == php->capacity)
	{
		int newcapacity=php->capacity == 0 ? 4 : 2 * php->capacity;
		HPDataType* tmp=(HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		php->a = tmp;
		php->capacity = newcapacity;
	}
	php->a[php->size++] = x;
	Ajustup(php->a, php->size-1);
}

Ajustup函数：

  •  二叉树的性质：child=2*parent+1

(可参考我的另外一篇博客：http://t.csdn.cn/GLlHN)

 如果child<parent时，child和parent交换，交换后child=parent。否则break跳出循环。以此循环，当child来到根节点时结束，即：下标为0。

void Ajustup(HPDataType*a, int child)
{//N*logN
	assert(a);
	//int child = n - 1;
	while (child > 0)
	{
		int parent = (child - 1) / 2;
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
		}
		else
		{
			break;
		}
	}
}

 交换可以写一个函数Swap来复用，会用到很多次。

void Swap(HPDataType* p1, HPDataType* p2)
{
	assert(p1);
	assert(p2);
	HPDataType tmp = 0;
		tmp = *p1;
		*p1 = *p2;
		*p2 = tmp;
}

HeapPop函数：

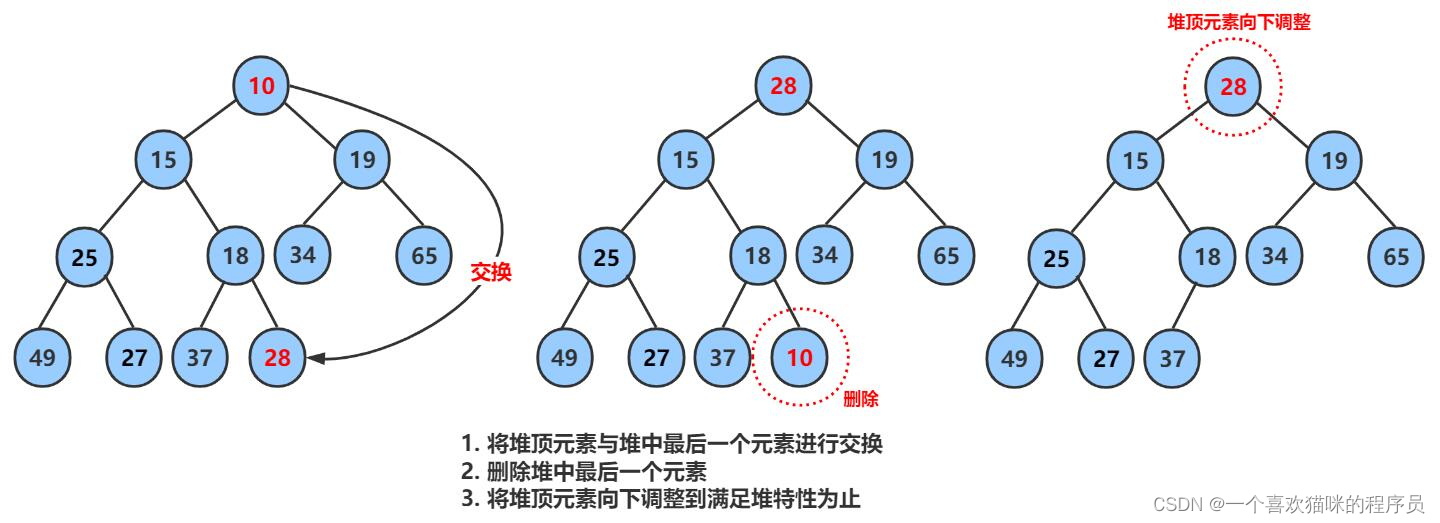
出数据只能是出堆顶的元素（根节点），否则没有什么意义。

当我们将根节点删除后，它的左子节点leftchild和右子节点rightchild谁来当根节点呢？ 并且我们还得维持它是一个堆，也就是维持它是一个完全二叉树。

假设左子节点大于右子节点时，让左子节点当根节点会出现什么情况呢？

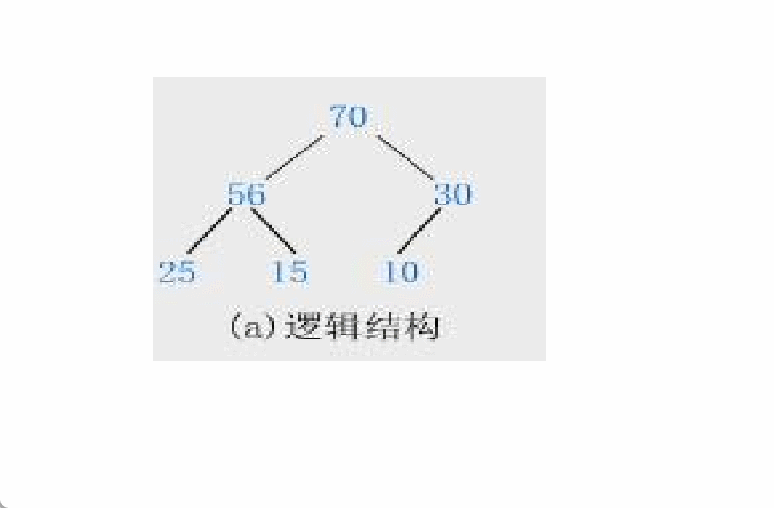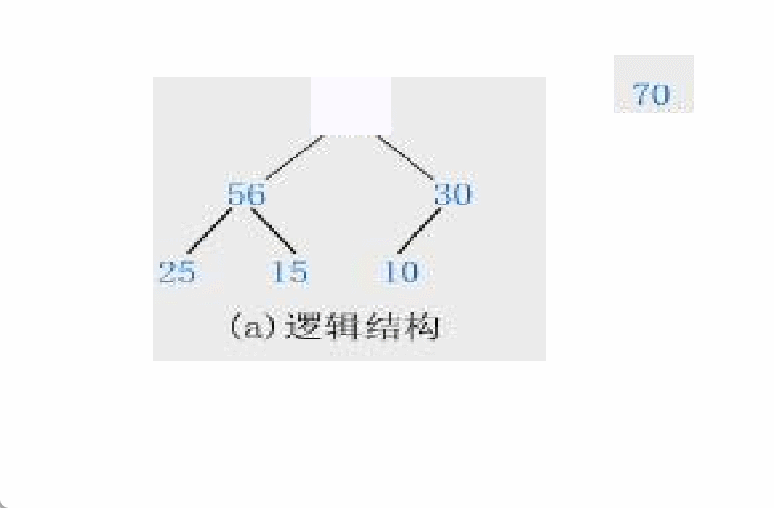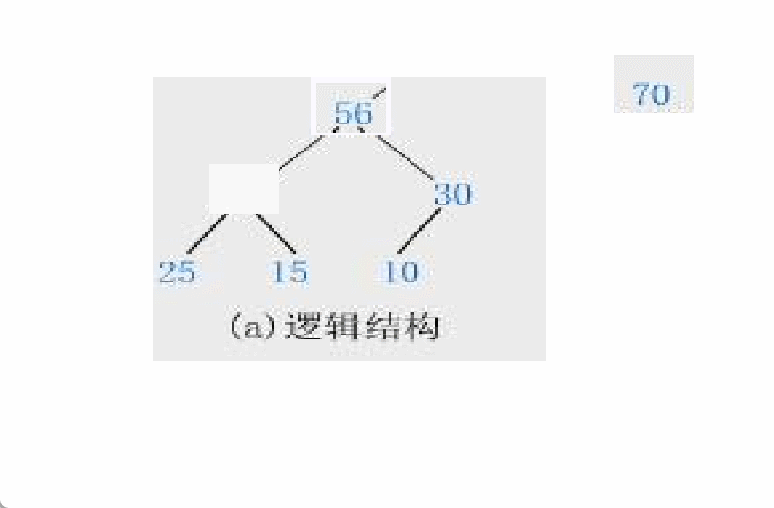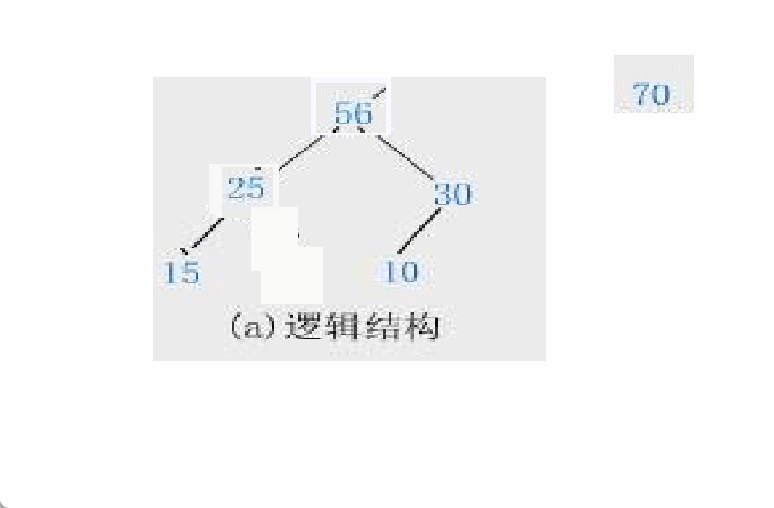显然这种方法是不可行的！！！

 换一种思路：

让第一个位置的值和最后一个位置的值，再size--不就相当于删除了嘛，但交换上去的值在根节点的位置上，我们无法维持是大堆的情况，因此还需要向下调整Ajustdown。

void HeapPop(HP* php)
{
	assert(php);
	assert(php->size > 0);
	Swap(&php->a[0], &php->a[php->size-1]);
	php->size--;
	Ajustdown(php->a, php->size-1 , 0);
}

Ajustdown函数： 

  • 由性质child=2*parent+1，反推：parent=（child-1）/2。

假设左子节点大，左子节点leftchild大于右子节点rightchild ，当左子节点小于右子节点，child++找到子节点大的那一个。

当parent>child时交换，parent=child、child=2*child+1。

void Ajustdown(HPDataType* a, int n,int parent)
{//O(N)
	assert(a);
	int child = 2 * parent+1;
	while (child<n)
	{
		if (child + 1 < n && a[child] < a[child + 1])//  <假设左子树大
		{
			child++;
		}
		if (a[child] > a[parent])//>大堆，<为小堆
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = child * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

HeapTop、HeapSize、HeapEmpty函数较为直接，就不做解释了。

HPDataType HeapTop(HP* php)
{
	assert(php);
	assert(php->size > 0);
	return php->a[0];
}
int HeapSize(HP* php)
{
	assert(php);
	return php->size;
}
bool HeapEmpty(HP* php)
{
	assert(php);
	if (php->size == 0)
		return true;
	else
		return false;
}

代码实现：

Heap.h文件：

#define  _CRT_SECURE_NO_WARNINGS
#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>
#include<string.h>
#include<time.h>
typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;
void Swap(HPDataType* p1, HPDataType* p2);
void HeapCreate(HP* php, HPDataType* a, int n);
void HeapPrintf(HP* php);
void HeapInit(HP* php);
void HeapDestroy(HP* php);
void HeapPush(HP* php, HPDataType x);
void HeapPop(HP* php);
HPDataType HeapTop(HP* php);
int HeapSize(HP* hp);
bool HeapEmpty(HP* hp);
void Ajustdown(HPDataType* a, int n, int parent); 
void Ajustup(HPDataType* a, int n);

Heap.c文件:

#include"Heap.h"
void HeapInit(HP* php)
{
	assert(php);
	php->capacity = 0;
	php->size = 0;
	php->a = NULL;
}
void HeapDestroy(HP* php)
{
	assert(php);
	assert(php->a);
	free(php->a);
	free(php);
}
void HeapPrintf(HP* php)
{
	assert(php);
	for (int i = 0; i < php->size; i++)
	{
		printf("%d ", php->a[i]);
	}
	printf("\n");
}
void Swap(HPDataType* p1, HPDataType* p2)
{
	assert(p1);
	assert(p2);
	HPDataType tmp = 0;
		tmp = *p1;
		*p1 = *p2;
		*p2 = tmp;
}
void Ajustup(HPDataType*a, int child)
{//N*logN
	assert(a);
	//int child = n - 1;
	while (child > 0)
	{
		int parent = (child - 1) / 2;
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
		}
		else
		{
			break;
		}
	}
}
void Ajustdown(HPDataType* a, int n,int parent)
{//O(N)
	assert(a);
	int child = 2 * parent+1;
	while (child<n)
	{
		if (child + 1 < n && a[child] < a[child + 1])//  <假设左子树大
		{
			child++;
		}
		if (a[child] > a[parent])//>大堆，<为小堆
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = child * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void HeapCreate(HP* php, HPDataType* a, int n)
{
	assert(php);
	HPDataType*tmp=(HPDataType*)malloc(sizeof(HPDataType) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	memcpy(php->a, tmp, sizeof(HPDataType)*n);
	php->size = php->capacity = n;
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		Ajustdown(php->a, n, i);
	}
}
void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	if (php->size == php->capacity)
	{
		int newcapacity=php->capacity == 0 ? 4 : 2 * php->capacity;
		HPDataType* tmp=(HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		php->a = tmp;
		php->capacity = newcapacity;
	}
	php->a[php->size++] = x;
	Ajustup(php->a, php->size-1);
}
void HeapPop(HP* php)
{
	assert(php);
	assert(php->size > 0);
	Swap(&php->a[0], &php->a[php->size-1]);
	php->size--;
	Ajustdown(php->a, php->size-1 , 0);
}
HPDataType HeapTop(HP* php)
{
	assert(php);
	assert(php->size > 0);
	return php->a[0];
}
int HeapSize(HP* php)
{
	assert(php);
	return php->size;
}
bool HeapEmpty(HP* php)
{
	assert(php);
	if (php->size == 0)
		return true;
	else
		return false;
}

Test.c文件：

#include"Heap.h"
void test1()
{
	HP php;
	HeapInit(&php);
	HeapPush(&php, 75);
	HeapPush(&php, 56);
	HeapPush(&php, 30);
	HeapPush(&php, 25);
	//HeapPop(&php);
	int a=HeapSize(&php);
	printf("%d\n", a);
	HeapPrintf(&php);
	HeapPush(&php, 100);
	HeapPrintf(&php);
	HeapPop(&php);
	HeapPrintf(&php);
	HeapDestroy(&php);
}
int main()
{
	test1();
	//test2();
	//test3();
	//test4();
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/97357.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【教学类-23-01】20221217《不会写学号的中班幼儿的学号描字贴》（中班描字)

【教学类-23-01】20221217《不会写学号的中班幼儿的学号描字贴》（中班描字)

成品样式&#xff1a; 每个孩子3页A4横板&#xff0c;供6次书写 打印样式&#xff1a; 背景需求&#xff1a; 前期进行6次的Python学具教学活动&#xff0c;对中3班幼儿书写学号和名字的情况评估&#xff1a; 筛选出10位需要练习学号的幼儿。 学号、名字需要持续性、强化性练…
阅读更多...
科技改变世界，科技改变世界杯

科技改变世界，科技改变世界杯

2022年11月20日&#xff0c;2022年卡塔尔世界杯&#xff08;英语&#xff1a;FIFA World Cup Qatar 2022&#xff09;在充满阿拉伯风情的开幕式中拉开了帷幕。 相比以往世界杯&#xff0c;今年卡塔尔世界杯在赛场上加设的黑科技&#xff0c;让我们在赛场上反复领略到了各种剧情…
阅读更多...
机器学习100天（四）：004 数据预处理之类别特征编码

机器学习100天（四）：004 数据预处理之类别特征编码

机器学习100天，今天讲的是：数据预处理之类别特征编码。 在上一节，我们对特征 X 的 NaN 值进行了平均数插值处理。 我们打开 X，查看第一列特征，国家这一列： 发现这一列特征都是字符串，例如：法国、德国、韩国。 大部分机器学习模型，字符串类别特征是不能用来直接进行…
阅读更多...
极简TS语法入门

极简TS语法入门

@关于TypeScript 微软/大项目：诸位，都按我定义好的类型撸码，谁也别TM瞎搞！哥也没时间跟你们浪费口舌了，凡瞎**搞的让丫连编译都通不过！（内心：不把C++的一点基因伸到前端被窝去你们当我微软是真软啊…）各种装X大厂：收到！立马装起来！什么？研发成本？这个我们不考虑的…
阅读更多...
LeetCode刷题复盘笔记—一文搞懂动态规划之5. 最长回文子串问题（动态规划系列第二十五篇）

LeetCode刷题复盘笔记—一文搞懂动态规划之5. 最长回文子串问题（动态规划系列第二十五篇）

今日主要总结一下动态规划的一道题目&#xff0c;5. 最长回文子串 题目&#xff1a;5. 最长回文子串 Leetcode题目地址 题目描述&#xff1a; 给你一个字符串 s&#xff0c;找到 s 中最长的回文子串。 如果字符串的反序与原始字符串相同&#xff0c;则该字符串称为回文字符串…
阅读更多...
Java项目：SSM失物招领网站信息管理系统

Java项目：SSM失物招领网站信息管理系统

作者主页&#xff1a;源码空间站2022 简介&#xff1a;Java领域优质创作者、Java项目、学习资料、技术互助 文末获取源码 项目介绍 本项目为后台管理系统&#xff0c;分为管理员与用户两种角色&#xff1b; 管理员角色包含以下功能&#xff1a; 管理员登录,修改个人信息,用户…
阅读更多...
零编程基础小白学习python应该看的python入门书籍

零编程基础小白学习python应该看的python入门书籍

Python作为目前的大势&#xff0c;是很多人转行的首选&#xff0c;会python的人工资通常都比较高。Python在人工智能、大数据、自动化运维、全栈开发方面有着得天独厚的优势。随着Python继续占领编程语言主流的趋势&#xff0c;全国各城市的招聘职位和薪资均会大幅度上涨。另外…
阅读更多...
使用java访问HDFS

使用java访问HDFS

文章目录利用Java编写程序访问HDFS1、创建Maven项目2、添加相关依赖3、创建日志属性文件4、启动集群HDFS服务5、在HDFS上创建文件利用Java编写程序访问HDFS 1、创建Maven项目 创建Maven项目 - HDFSDemo 单击【Create】按钮 2、添加相关依赖 在pom.xml文件里添加hadoop和…
阅读更多...
【问答篇】Java 基础篇面试题（二）

【问答篇】Java 基础篇面试题（二）

每天进步一点~ 01、问&#xff1a;PreparedStatement与Statement的区别&#xff1f; 答&#xff1a; PreparedStatement是预编译语句执行者&#xff0c;数据库对sql语句进行预编译&#xff1b;Statement是执行时对sql语句进行编译 Statement存在sql注入的问题&#xff0c;Prep…
阅读更多...
25.读写文件

25.读写文件

到目前为止&#xff0c;我们讨论了如何处理数据&#xff0c; 以及如何构建、训练和测试深度学习模型。 然而&#xff0c;有时我们希望保存训练的模型&#xff0c; 以备将来在各种环境中使用&#xff08;比如在部署中进行预测&#xff09;。 此外&#xff0c;当运行一个耗时较…
阅读更多...
English Learning - L1-3 从此没有不会的表达(上) 2022.12.12 周一

English Learning - L1-3 从此没有不会的表达(上) 2022.12.12 周一

English Learning - L1-3 从此没有不会的表达&#xff08;上&#xff09; 2022.12.12 周一4 名词性从句名词性从句的类型4.1 各种从句的变身4.1.1 陈述句的变身一个严肃的问题&#xff1a;为什么要加 that ?那什么情况下&#xff0c;that 是可以省略的&#xff1f;特殊动词4.1…
阅读更多...
Okhttp源码分析实践（三）【WebDemo的简单实现】

Okhttp源码分析实践（三）【WebDemo的简单实现】

我们继续深入探索okhttp的知识点和面。本章，我们一起来实现一些简单的服务端Demo API，至于为什么，其实之前也说过，一方面是为了使我们之前所学的http的基础知识得到实践运用，另外一方面，是为了我们之后自己编写实现okhttp时，避免不了肯定要做很多API测试，免费的测试api…
阅读更多...
vue3 provide与inject进行状态管理

vue3 provide与inject进行状态管理

vue3 provide与inject进行状态管理 一、数据仓库准备 在store–>新建index.js文件&#xff0c;作为仓库数据 状态集中管理数据实现响应式ref reactive—>对象中存储状态msg,age,counter import {reactive} from vue const store{//数据state:reactive({msg:"Hello …
阅读更多...
WebRTC：P2P音视频通话基础概述

WebRTC：P2P音视频通话基础概述

前言 本篇文章参考WebRTC基础知识详解_签约计划_IT酷盖_InfoQ写作社区&#xff0c;介绍了P2P音视频通信的场景下的一些基础知识&#xff0c;包括WebRTC的基本架构、协议栈&#xff0c;一对一通话基础&#xff0c;和一对一通话原理三部分。 WebRTC基本架构 WebRTC 的组件架构分…
阅读更多...
css样式补充，项目前置认知，精灵图，背景图片大小，阴影，过渡，SEO简介

css样式补充，项目前置认知，精灵图，背景图片大小，阴影，过渡，SEO简介

1、css样式补充&#xff0c;项目前置认知&#xff0c;字体图标 学习目标&#xff1a; u 能够在网页中使用 精灵图 u 能够使用 背景大小属性 &#xff0c;设置背景图片的大小 u 能够认识 CSS书写顺序&#xff0c;提高代码专业性和浏览器渲染性能 u 能够使用的专业方式完成 项目结…
阅读更多...
1_MyBatis入门-1_认识框架

1_MyBatis入门-1_认识框架

原生JDBC实现CURD的问题 1 编码繁琐 2 需要我们自己将结果集映射成对象 3 性能不太好 连接池 缓存 4 SQL语句和java代码的耦合度特别高 5 … … MyBatis 本是Apache的一个开源项目iBatis, 2010年这个项目由Apache Software Foundation 迁移到了Google Code&#xff0c;且…
阅读更多...
java高级--Elasticsearch

java高级--Elasticsearch

一、概述搜索引擎 1.1 什么是搜索引擎 概念&#xff1a;用户输入想要的关键词&#xff0c;返回含有该关键词的所有信息。 场景&#xff1a; 1、互联网搜索&#xff1a;谷歌、百度、各种新闻首页 2、 站内搜索&#xff08;垂直搜索&#xff09;&#xff1a;企业OA查询订单、人员…
阅读更多...
Linx基础（8）shell基础

Linx基础（8）shell基础

该文章主要为完成实训任务&#xff0c;详细实现过程及结果见【参考文章】 参考文章&#xff1a;https://howard2005.blog.csdn.net/article/details/127139576?spm1001.2014.3001.5502 文章目录一、常用shell命令1. 管道命令任务1、查看/etc目录信息前5行信息任务2、查看/etc/…
阅读更多...
【谷歌新作】Transformer杀入机器人领域，RT-1：97%成功率，轻松完成700多条控制指令

【谷歌新作】Transformer杀入机器人领域，RT-1：97%成功率，轻松完成700多条控制指令

谷歌机器人团队等在机器人领域构建了一个多任务 transformer 模型&#xff0c;显著改进了对新任务、环境和对象的零样本泛化。 我们知道&#xff0c;机器学习&#xff08;ML&#xff09;多个子领域&#xff08;如 NLP 和 CV&#xff09;的最新重大进展通过一种共享的通用方法实…
阅读更多...
ZYNQ之FPGA学习----SPI协议驱动模块仿真实验

ZYNQ之FPGA学习----SPI协议驱动模块仿真实验

1 SPI通信协议简介 SPI通信协议基础知识学习&#xff1a;硬件设计基础----通信协议SPI 2 实验任务 设计SPI驱动模块&#xff0c;并进行仿真验证&#xff0c;观察仿真波形 3 实验设计 3.1 创建工程 新建工程&#xff0c;操作如图所示&#xff1a; 输入工程名和路径&#x…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023