目录
1.算法描述
2.仿真效果预览
3.MATLAB核心程序
4.完整MATLAB
1.算法描述
聚类就是按照某个特定标准把一个数据集分割成不同的类或簇,使得同一个簇内的数据对象的相似性尽可能大,同时不在同一个簇中的数据对象的差异性也尽可能地大。即聚类后同一类的数据尽可能聚集到一起,不同类数据尽量分离。主要的聚类算法可以划分为如下几类:划分方法、层次方法、基于密度的方法、基于网格的方法以及基于模型的方法。下面主要对k-means聚类算法、凝聚型层次聚类算法、神经网络聚类算法之SOM,以及模糊聚类的FCM算法通过通用测试数据集进行聚类效果的比较和分析。
k-means是划分方法中较经典的聚类算法之一。由于该算法的效率高,所以在对大规模数据进行聚类时被广泛应用。目前,许多算法均围绕着该算法进行扩展和改进。k-means算法以k为参数,把n个对象分成k个簇,使簇内具有较高的相似度,而簇间的相似度较低。k-means算法的处理过程如下:首先,随机地 选择k个对象,每个对象初始地代表了一个簇的平均值或中心;对剩余的每个对象,根据其与各簇中心的距离,将它赋给最近的簇;然后重新计算每个簇的平均值。 这个过程不断重复,直到准则函数收敛。
算法流程:
输入:包含n个对象的数据和簇的数目k;
输出:n个对象到k个簇,使平方误差准则最小。
步骤:
(1) 任意选择k个对象作为初始的簇中心;
(2) 根据簇中对象的平均值,将每个对象(重新)赋予最类似的簇;
(3) 更新簇的平均值,即计算每个簇中对象的平均值;
(4) 重复步骤(2)、(3)直到簇中心不再变化;
层次聚类算法
根据层次分解的顺序是自底向上的还是自上向下的,层次聚类算法分为凝聚的层次聚类算法和分裂的层次聚类算法。 凝聚型层次聚类的策略是先将每个对象作为一个簇,然后合并这些原子簇为越来越大的簇,直到所有对象都在一个簇中,或者某个终结条件被满足。绝大多数层次聚类属于凝聚型层次聚类,它们只是在簇间相似度的定义上有所不同。
算法流程:
注:以采用最小距离的凝聚层次聚类算法为例:
(1) 将每个对象看作一类,计算两两之间的最小距离;
(2) 将距离最小的两个类合并成一个新类;
(3) 重新计算新类与所有类之间的距离;
(4) 重复(2)、(3),直到所有类最后合并成一类。
神经网络的训练主要包括两个部分:正向传播和反向传播两个过程。正向传播得到损失值,反向传播得到梯度。最后通过梯度值完成权值更新(其中梯度就是一个偏导数向量)。采用反向传播算法构建神经网络的模型,可以实现扑克牌数据集的多分类问题。搭建神经网络的主要步骤:
- 训练的数据
- 定义节点准备接收数据
- 定义神经层:隐藏层和预测层
- 定义 loss 表达式
- 选择 optimizer 使 loss 达到最小
- 保存训练结果 对扑克牌数据集进行简单的预处理,读取预处理后的数据加载到神经网络中,搭建有 4 个隐藏层的神经网络。神经网络与感知器的最大的一个区别在于:感知器的激活函数是节阶跃的而神经网络的激活函数是非线性的,从而给神经网络引入了非线性的因素。在对扑克牌的数据集进行训练是使用 ReLU 为每个隐藏层的激活函数,式 (1) 是 ReLU 的函数表达式,如图 1.1 是 ReLU 的函数图像。
在模糊神经网络设计中,模糊规则的建立是系统设计的瓶颈问题,所以有关神经网络与模糊系统相结合的研究大多集中在模糊神经网络的建模,模糊神经网络结构和算法的研究是国内外学者研究的热点,新模糊神经网络模型和学习算法不断涌现。
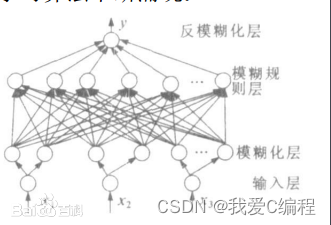
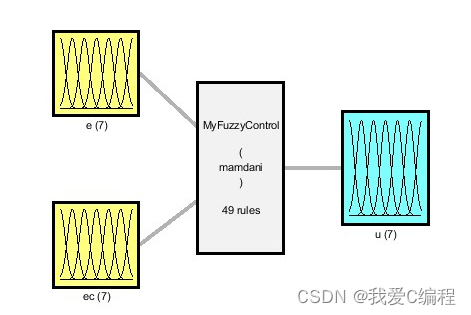
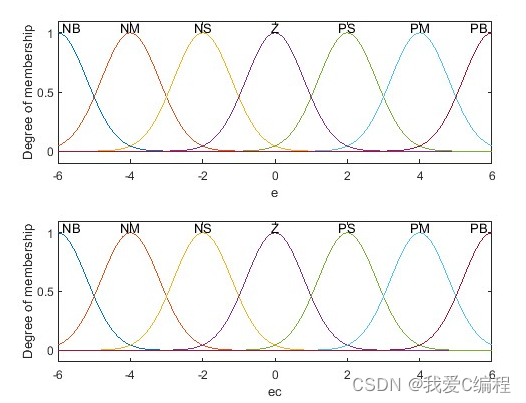
模糊神经网络一般结构如图1所示。第一层为输入层,缓存输入信号。第二层为模糊化层,对输入信号进行模糊化。第三层为模糊规则层。第四层为模糊决策层,主要针对满足一定条件的量进行分类并将模糊量去模糊化。第五层为输出层,输出运算结果。
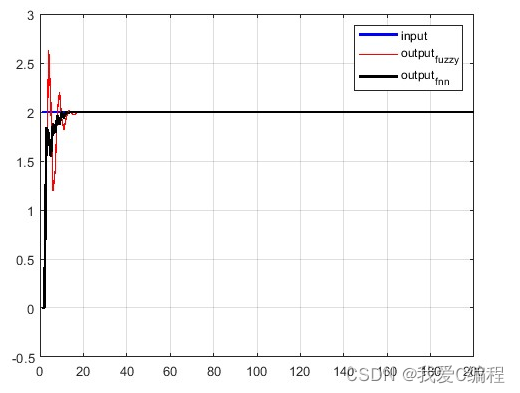
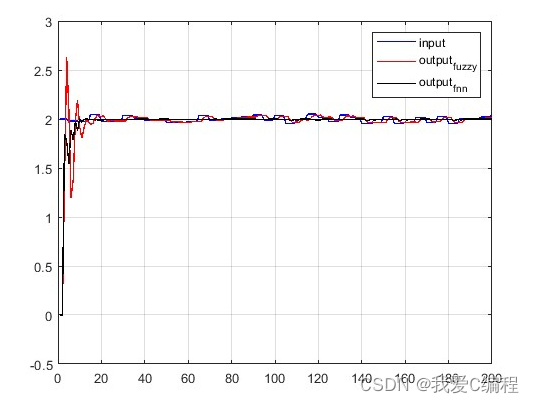
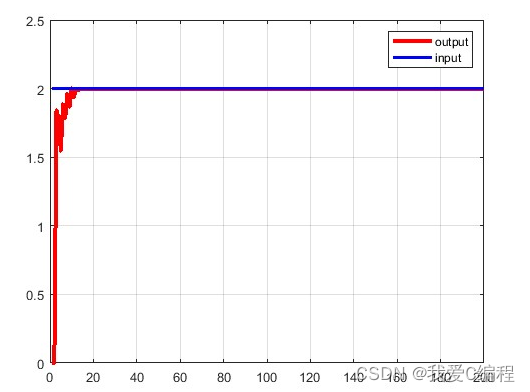
2.仿真效果预览
matlab2022a仿真结果如下:


3.MATLAB核心程序
A = [ 3.945 0 1;
15.063 -8.05 0;
6.943 0 -1];
A = A/max(max(abs(A)));
C2 = [0 0;
0 1;
1 0];
Ku = 0.7;
Ke = 1;
Kec = 1;
K = 1;
%闭环控制器
for k=1:SIM_times
k
time(k) = k*ts;
%定义输入信号
din(k) = 2;
%定义输出信号
%定义干扰
q = 0.012 + (0.142 - 0.012) * rand(1,1);
%定义输出
Tmp = A * [x,s,o]' + C2 * [(1+Ku)*u1,q]';
o = Tmp(3);
yout(k) = o;
e(k) = yout(k) - din(k);
x1 =(1-exp(-10*Ke*e1))/(1+exp(-10*Ke*e1));
x2 =(1-exp(-Kec*ec))/(1+exp(-Kec*ec));
%第1层输出
for i=1:7
o11(i) = x1;
o12(i) = x2;
end
o1=[o11;o12];
%第2层输出
for i=1:2
for j=1:7
z1(i,j) =-((o1(i,j)-a(i,j))^2)/(b(i,j));
o2(i,j) = exp(z1(i,j));
end
end
%第3层输出
for j=1:7
for l=1:7
o3((j-1)*7+l)=o2(1,j)*o2(2,l);
end
end
%第4层输出
I=0;
for i=1:49
I = I + o3(i)*Weight(i);
end
o4 = I/(sum(o3));
u(k) = o4;
u1 =-u(k);
e1 = e(k);
ec = e(k)-error1;
error1 = e(k);
%梯度下降法调整权值
for i=1:49
dwp = e1*du*o3(i)/(sum(o3));
%迭代
Weight(i) = Weight(i) + eta*dwp;
end
%中心值更新
da11=zeros(1,7);
for j=1:7
for l=1:7
da11(j) = da11(j)+(o2(2,l)*((Weight((j-1)*7+l)*sum(o3))-I));
end
da12(1,j) = -e1*du*(2*(o1(1,j)-a(1,j))*(o2(1,j)))/((b(1,j)^2)*(sum(o3))^2);
da1(j) = (da12(1,j))*(da11(j));
end
da21 = zeros(1,7);
for j=1:7
for l=1:7
da21(j) = da21(j)+(o2(1,l)*((Weight((l-1)*7+j)*sum(o3))-I));
end
da22(2,j) = -e1*du*(2*(o1(2,j)-a(2,j))*(o2(2,j))/((b(2,j)^2)*(sum(o3))^2));
da2(j) = (da22(2,j))*(da21(j));
end
da=[da1;da2];
for i=1:2
for j=1:7
a(i,j)=a(i,j)-eta*da(i,j);
end
end
a_s(:,:,k) = a;
if k == 1
a_(:,:,k) = a_s(:,:,1);
else
for i = 1:2
for j = 1:7
dist_tmp(i,j) = (a_s(i,j,k) - a_(i,j))^2;
end
end
dist = sqrt(sum(sum(dist_tmp)));
if dist < 0.1
tmps(:,:,1) = a_(:,:,k-1);
tmps(:,:,2) = a_s(:,:,k);
a_(:,:,k) = mean(tmps(:,:,1:2),3);
else
a_(:,:,k) = a_(:,:,k-1);
end
end
a = a_(:,:,k);
%宽度更新
db11=zeros(1,7);
for j=1:7
for l=1:7
db11(j)=db11(j)+(o2(2,l)*((Weight((j-1)*7+l)*sum(o3))-I));
end
db12(1,j)=-e1*du*(2*(o1(1,j)-a(1,j))^2)*(o2(1,j))/((b(1,j)^3)*(sum(o3))^2);
db1(j)=(db12(1,j))*(db11(j));
end
db21=zeros(1,7);
for j=1:7
for l=1:7
db21(j)=db21(j)+(o2(1,l)*((Weight((l-1)*7+j)*sum(o3))-I));
end
db22(2,j)=-e1*du*(2*(o1(2,j)-a(2,j))^2)*(o2(2,j))/((b(2,j)^3)*(sum(o3))^2);
db2(j)=(db22(2,j))*(db21(j));
end
db=[db1;db2];
for i=1:2
for j=1:7
b(i,j)=b(i,j)-eta*db(i,j);
end
end
b_s(:,:,k) = b;
if k == 1
b_(:,:,k) = b_s(:,:,1);
else
for i = 1:2
for j = 1:7
dist_tmp(i,j) = (b_s(i,j,k) - b_(i,j))^2;
end
end
dist = sqrt(sum(sum(dist_tmp)));
if dist < 0.1
tmps(:,:,1) = b_(:,:,k-1);
tmps(:,:,2) = b_s(:,:,k);
b_(:,:,k) = mean(tmps(:,:,1:2),3);
else
b_(:,:,k) = b_(:,:,k-1);
end
end
b = b_(:,:,k);
%算法
s11 = y1;
s12 = y2;
s13 = u1;
s14 = u2;
s1 =[s11;s12;s13;s14];
for i=1:5
net2(i) = w2(i,:)*s1 + theta2(i);
s2(i) = (1-exp(-net2(i)))/(1+exp(-net2(i)));
end
net3 = w3*s2+theta3;
yg = am*(1-exp(-net3))/(1+exp(-net3));
for i=1:5
delta2(i)=0.5*(1-s2(i))*(1+s2(i));
end
delta3=0.5*am*(1-yg/am)*(1+yg/am);
for i=1:5
theta22(i) = theta2(i)-theta21(i);
theta21(i) = theta2(i);
theta2(i) = theta2(i)+eta1*(yout(k)-yg)*delta3*w3(i)*delta2(i)+beta1*theta22(i);
end
theta32 = theta3-theta31;
theta31 = theta3;
theta3 = theta3+eta1*(yout(k)-yg)*delta3+beta1*theta32;
for i=1:5
for j=1:4
w22(i,j) = w2(i,j)-w21(i,j);
w21(i,j) = w2(i,j);
w2(i,j) = w2(i,j)-eta1*(yout(k)-yg)*delta3*w3(i)*delta2(i)*s1(j)+beta1*w22(i,j);
end
w32(i) = w3(i)-w31(i);
w31(i) = w3(i);
w3(i) = w3(i)-eta1*(yout(k)-yg)*delta3*s2(i)+beta1*w32(i);
end
a2 = am-a1;
a1 = am;
am = am+eta1*(yout(k)-yg)*yg/am+beta1*a2;
sum1 = 0;
for i=1:5
sum1 = sum1 + w3(i)*delta2(i)*w2(i,3);
end
du = delta3*sum1;
end
05_006_m4.完整MATLAB
V


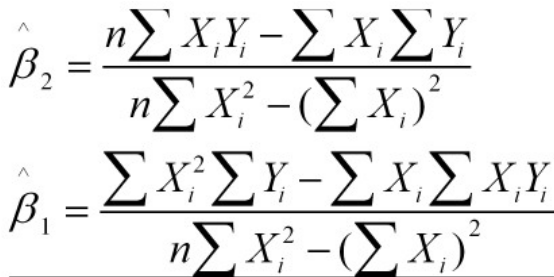

![[附源码]Nodejs计算机毕业设计基于社区疫情防控管理系统Express(程序+LW)](https://img-blog.csdnimg.cn/1498817b84be41ccbb699c3b260f7ae2.png)