文章目录
- 导数积分公式表🎈
- 积分计算器
- pictures version
- markdown Table version🎈🎈🎈🎈
- Notes
- 补充
- 几个积分公式的推导和记忆方法🎈
- 幂函数积分的一些常用特值扩充🎃
- 附:表格原码
导数积分公式表🎈
积分计算器
- 积分计算@图像
pictures version
markdown Table version🎈🎈🎈🎈
-
渲染不正常的,末尾附带原码,自行用typora渲染
f ( x ) f(x) f(x) f ′ ( x ) = d d x f ( x ) f'(x)=\frac{d}{\mathrm{d}x}f(x) f′(x)=dxdf(x) ∫ f ( x ) d x \displaystyle\int{f(x)}\mathrm{d}x ∫f(x)dx Note k k k 0 k x + C kx+C kx+C x 1 2 = x x^{\frac{1}{2}}=\sqrt{x} x21=x 1 2 x = 1 2 x − 1 2 \frac{1}{2\sqrt{x}}=\frac{1}{2}x^{-\frac{1}{2}} 2x1=21x−21 2 3 x 3 2 + C \frac{2}{3}x^{\frac{3}{2}}+C 32x23+C 1 x = x − 1 \frac{1}{x}=x^{-1} x1=x−1 − 1 x 2 = − x − 2 -\frac{1}{x^2}=-x^{-2} −x21=−x−2 $\ln{ x x a x^{a} xa a x a − 1 ax^{a-1} axa−1 1 a + 1 x a + 1 + C \frac{1}{a+1}x^{a+1}+C a+11xa+1+C a ≠ − 1 a\neq{-1} a=−1 a x a^x ax a x ln a a^x\ln{a} axlna 1 ln a a x + C \frac{1}{\ln{a}}a^x+C lna1ax+C a > 0 , a ≠ 1 a>0, a\neq 1 a>0,a=1 e x e^x ex e x e^x ex e x + C e^x+C ex+C log a x \log_a{x} logax 1 x ln a \frac{1}{x\ln{a}} xlna1 x log a x − 1 ln a x + C x\log_{a}x-\frac{1}{\ln{a}}x+C xlogax−lna1x+C 积分使用分部积分法 ln x \ln{x} lnx 1 x \frac{1}{x} x1 x ln x − x + C x\ln{x}-x+C xlnx−x+C $(\ln sin x \sin{x} sinx cos x \cos{x} cosx − cos x + C -\cos{x}+C −cosx+C cos x \cos{x} cosx − sin x -\sin{x} −sinx sin x + C \sin{x}+C sinx+C sec x \sec{x} secx sec x tan x \sec{x}\tan{x} secxtanx $\ln{ \sec{x}+\tan{x} csc x \csc{x} cscx − csc x cot x -\csc{x}\cot{x} −cscxcotx $-\ln \csc{x}+\cot{x} tan x \tan{x} tanx sec 2 x \sec^2{x} sec2x $-\ln \cos{x} cot x \cot{x} cotx − csc 2 x -\csc^2{x} −csc2x $\ln \sin{x} sin 2 x \sin^2{x} sin2x x 2 − sin 2 x 4 + C \frac{x}{2}-\frac{\sin{2x}}{4}+C 2x−4sin2x+C sin 2 x = 1 2 ( 1 − cos 2 x ) \sin^2{x}=\frac{1}{2}(1-\cos{2x}) sin2x=21(1−cos2x) cos 2 x \cos^2{x} cos2x x 2 + sin 2 x 4 + C \frac{x}{2}+\frac{\sin{2x}}{4}+C 2x+4sin2x+C cos 2 x = 1 2 ( 1 + cos 2 x ) \cos^2{x}=\frac{1}{2}(1+\cos{2x}) cos2x=21(1+cos2x) sec 2 x \sec^2{x} sec2x tan x + C \tan{x}+C tanx+C csc 2 x \csc^2{x} csc2x − cot x + C -\cot{x}+C −cotx+C tan 2 x \tan^2{x} tan2x tan x − x + C \tan{x}-x+C tanx−x+C tan 2 x = sec 2 x − 1 \tan^2{x}=\sec^2x-1 tan2x=sec2x−1 cot 2 x \cot^2{x} cot2x − cot x − x + C -\cot{x}-x+C −cotx−x+C cot 2 x = csc 2 x − 1 \cot^2{x}=\csc^2{x}-1 cot2x=csc2x−1 sec x tan x \sec{x}\tan{x} secxtanx sec x + C \sec{x}+C secx+C csc x cot x \csc{x}\cot{x} cscxcotx − csc x + C -\csc{x}+C −cscx+C arcsin x \arcsin{x} arcsinx 1 1 − x 2 \frac{1}{\sqrt{1-x^2}} 1−x21 arccos x \arccos{x} arccosx − 1 1 − x 2 -\frac{1}{\sqrt{1-x^2}} −1−x21 arctan x \arctan{x} arctanx 1 1 + x 2 \frac{1}{1+x^2} 1+x21 a r c cot x \mathrm{arc}\cot{x} arccotx − 1 1 + x 2 -\frac{1}{1+x^2} −1+x21 1 x 2 ± a 2 \frac{1}{\sqrt{x^2\pm a^2}} x2±a21 $\ln {x}+\sqrt{x^2\pm a^2} 1 a 2 − x 2 \frac{1}{\sqrt{a^2-x^2}} a2−x21 arcsin x a + C \arcsin{\frac{x}{a}}+C arcsinax+C 1 1 − x 2 \frac{1}{\sqrt{1-x^2}} 1−x21 arcsin x + C \arcsin{x}+C arcsinx+C 1 x 2 + a 2 \frac{1}{x^2+a^2} x2+a21 1 a arctan x a + C \frac{1}{a}\arctan{\frac{x}{a}}+C a1arctanax+C 1 1 + x 2 \frac{1}{1+x^2} 1+x21 arctan x + C \arctan{x}+C arctanx+C 1 x 2 − a 2 \frac{1}{x^2-a^2} x2−a21 $\frac{1}{2a}\ln \frac{x-a}{x+a} a 2 − x 2 \sqrt{a^2-x^2} a2−x2 1 2 ( a 2 arcsin x a + x a 2 − x 2 ) + C \frac{1}{2}(a^2\arcsin{\frac{x}{a}}+x\sqrt{a^2-x^2})+C 21(a2arcsinax+xa2−x2)+C $(a> x 2 ± a 2 \sqrt{x^2\pm{}a^2} x2±a2 $\frac{1}{2}(x\sqrt{x2\pm{}a2}\pm{}a^2\ln x+\sqrt{x2\pm{}a2}
Notes
-
NoteA:
- csc x − cot x = ( csc x + cot x ) − 1 1 sin x − cos x sin x = 1 1 sin x + cos x sin x 1 − cos x sin x = sin x 1 + cos x 即 1 − cos 2 x = sin 2 x , 这显然成立 \csc{x}-\cot{x}=(\csc{x}+\cot{x})^{-1} \\ \frac{1}{\sin{x}}-\frac{\cos{x}}{\sin{x}}=\frac{1}{\frac{1}{\sin{x}}+\frac{\cos{x}}{\sin{x}}} \\ \frac{1-\cos{x}}{\sin{x}}=\frac{\sin{x}}{1+\cos{x}} 即 \\1-\cos^2{x}=\sin^2{x},这显然成立 cscx−cotx=(cscx+cotx)−1sinx1−sinxcosx=sinx1+sinxcosx1sinx1−cosx=1+cosxsinx即1−cos2x=sin2x,这显然成立
补充
-
( ln ∣ x ∣ ) ′ = 1 x ( x ≠ 0 ) (\ln|x|)'=\frac{1}{x}(x\neq{0}) (ln∣x∣)′=x1(x=0)
-
分段分析,去掉绝对值
- { ln x , x > 0 ln ( − x ) , x < 0 分别求导 : { 1 x , x > 0 1 − x ( − 1 ) = 1 x , x < 0 ∴ ( ln ∣ x ∣ ) ′ = 1 x , x ≠ 0 \\ \begin{cases} \ln{x},x>0 \\ \ln{(-x)},x<0 \end{cases} \\ 分别求导: \begin{cases} \frac{1}{x},x>0 \\ \frac{1}{-x}{(-1)}=\frac{1}{x},x<0 \end{cases} \\ \therefore (\ln|x|)'=\frac{1}{x},x\neq{0} {lnx,x>0ln(−x),x<0分别求导:{x1,x>0−x1(−1)=x1,x<0∴(ln∣x∣)′=x1,x=0
-
几个积分公式的推导和记忆方法🎈
x 2 ± a 2 x^2\pm{a^2} x2±a2
-
∫ 1 x 2 ± a 2 d x = ln ∣ x + x 2 ± a 2 ∣ + C \int \frac{1}{\sqrt{x^2\pm a^2}}dx=\ln|x+\sqrt{x^2\pm a^2}|+C ∫x2±a21dx=ln∣x+x2±a2∣+C
- p = p ± = x 2 ± A = x 2 ± a 2 ; A = a 2 p=p_{\pm}=\sqrt{x^2\pm A}=\sqrt{x^2\pm a^2};A=a^2 p=p±=x2±A=x2±a2;A=a2
- ∫ 1 x 2 − a 2 d x = ∫ 1 p d x = ln ∣ x + p ∣ + C ★ \int \frac{1}{\sqrt{x^2-a^2}}dx=\int \frac{1}{p}dx=\ln|x+p|+C\bigstar ∫x2−a21dx=∫p1dx=ln∣x+p∣+C★
- 可由三角换元推导
- 形如表达式 ∫ 1 x 2 + A \int \frac{1}{\sqrt{x^2+A}} ∫x2+A1的形式出现,就可以套用本公式
a 2 − x 2 \sqrt{a^2-{x^2}} a2−x2
-
∫ a 2 − x 2 d x = a 2 2 a r c s i n x a + 1 2 x a 2 − x 2 + C = 1 2 ( a 2 a r c s i n x a + x a 2 − x 2 ) + C \int \sqrt{a^2-x^2}dx=\frac{a^2}{2}arcsin{\frac{x}{a}}+\frac{1}{2}x\sqrt{a^2-x^2}+C=\frac{1}{2}(a^2arcsin{\frac{x}{a}}+x\sqrt{a^2-x^2})+C ∫a2−x2dx=2a2arcsinax+21xa2−x2+C=21(a2arcsinax+xa2−x2)+C
-
p = a 2 − x 2 p=\sqrt{a^2-x^2} p=a2−x2
-
∫ p d x = 1 2 a 2 ∫ 1 p d x + 1 2 x p = 1 2 ( a 2 ∫ 1 p d x + x p ) + C \int p dx=\frac{1}{2}a^2\int \frac{1}{p}dx+\frac{1}{2}xp=\frac{1}{2}(a^2\int \frac{1}{p}dx+xp)+C ∫pdx=21a2∫p1dx+21xp=21(a2∫p1dx+xp)+C
-
x 2 − a 2 \sqrt{x^2-a^2} x2−a2
-
∫ x 2 − a 2 d x = 1 2 ( x x 2 − a 2 − a 2 ln ∣ x + x 2 − a 2 ∣ ) \int \sqrt{x^2-a^2}dx=\frac{1}{2}(x\sqrt{x^2-a^2}-a^2\ln |x+\sqrt{x^2-a^2}|) ∫x2−a2dx=21(xx2−a2−a2ln∣x+x2−a2∣)
-
分部积分
-
S = ∫ x 2 − a 2 d x = x x 2 − a 2 − ∫ x d x 2 − a 2 为例方便说明推导和简洁性 , 提前给出如下标记 ( 表达式记号 ) A = x x 2 − a 2 B = ∫ x d x 2 − a 2 P = x 2 − a 2 Q = a 2 ∫ 1 x 2 − a 2 d x = a 2 ln ∣ x + x 2 − a 2 ∣ \\ \begin{aligned} S&=\int \sqrt{x^2-a^2}dx \\ &=x\sqrt{x^2-a^2}-\int xd\sqrt{x^2-a^2} \end{aligned} \\为例方便说明推导和简洁性,提前给出如下标记(表达式记号) \\ \begin{aligned} \\A&=x\sqrt{x^2-a^2} \\B&=\int xd\sqrt{x^2-a^2} \\P&=\sqrt{x^2-a^2} \\Q&=a^2\int\frac{1}{\sqrt{x^2-a^2}}dx=a^2\ln |x+\sqrt{x^2-a^2}| \end{aligned} S=∫x2−a2dx=xx2−a2−∫xdx2−a2为例方便说明推导和简洁性,提前给出如下标记(表达式记号)ABPQ=xx2−a2=∫xdx2−a2=x2−a2=a2∫x2−a21dx=a2ln∣x+x2−a2∣
-
B = ∫ x d x 2 − a 2 = ∫ x 2 x 2 − a 2 d x = 分子 + 0 = − a 2 + a 2 ∫ x 2 − a 2 + a 2 x 2 − a 2 d x = ∫ x 2 − a 2 d x + a 2 ∫ 1 x 2 − a 2 d x = S + Q \begin{aligned} B &=\int xd\sqrt{x^2-a^2}\\ &=\int \frac{x^2}{\sqrt{x^2-a^2}}dx \\ &\xlongequal{分子+0=-a^2+a^2}\int \frac{x^2-a^2+a^2}{\sqrt{x^2-a^2}}dx\\ &=\int\sqrt{x^2-a^2}dx+a^2\int\frac{1}{\sqrt{x^2-a^2}}dx\\ \\ &=S+Q \end{aligned} B=∫xdx2−a2=∫x2−a2x2dx分子+0=−a2+a2∫x2−a2x2−a2+a2dx=∫x2−a2dx+a2∫x2−a21dx=S+Q
-
S = A − B = A − S − Q 2 S = A − Q → S = 1 2 ( A − Q ) S = 1 2 ( x x 2 − a 2 − a 2 ln ∣ x + x 2 − a 2 ∣ ) \\S=A-B=A-S-Q \\2S=A-Q \to S=\frac{1}{2}(A-Q) \\S=\frac{1}{2}(x\sqrt{x^2-a^2}-a^2\ln |x+\sqrt{x^2-a^2}|) S=A−B=A−S−Q2S=A−Q→S=21(A−Q)S=21(xx2−a2−a2ln∣x+x2−a2∣)
-
-
a 2 + x 2 \sqrt{a^2+x^2} a2+x2
∫ a 2 + x 2 d x = 1 2 ( x a 2 + x 2 + a 2 ln ∣ a 2 + x 2 + x ∣ ) + C \displaystyle\int \sqrt{a^2+x^2}dx=\frac{1}{2}(x\sqrt{a^2+x^2}+a^2 \ln|\sqrt{a^2+x^2}+x|)+C ∫a2+x2dx=21(xa2+x2+a2ln∣a2+x2+x∣)+C
- 利用三角换元配合分部积分法可以推导
- ∫ s e c 3 t d t = 1 2 ( s e c x t a n x + ln ∣ s e c x + t a n x ∣ ) + C \int sec^3t\ dt=\frac{1}{2}(secxtanx+\ln |secx+tanx|)+C ∫sec3t dt=21(secxtanx+ln∣secx+tanx∣)+C
- p = a 2 + x 2 p=\sqrt{a^2+x^2} p=a2+x2
- A = x p A=xp A=xp
- Q = a 2 ln ∣ x + p ∣ Q=a^2\ln|x+p| Q=a2ln∣x+p∣
- S = 1 2 ( A + Q ) + C S=\frac{1}{2}(A+Q)+C S=21(A+Q)+C
幂函数积分的一些常用特值扩充🎃
-
o v e r h e a d : 积分升幂 ( 特例 : 1 x ) ∫ x k d x = 1 k + 1 x k + 1 + C = x p p + C , p = k + 1 ∫ 1 x d x = ∫ x − 1 d x = l n ∣ x ∣ + C ∫ 1 x 2 d x = ∫ x − 2 d x = − x − 1 + C = − 1 x + C ∫ 1 x d x = ∫ x − 1 2 d x = 2 x 1 2 + C = 2 x + C ∫ x d x = ∫ x 1 2 d x = 2 3 x 3 2 + C o v e r h e a d : 求导降幂 ( x k ) ′ = k x k − 1 ( 1 x ) ′ = ( x − 1 ) ′ = − x − 2 = − 1 x 2 ( 1 x 2 ) ′ = ( x − 2 ) ′ = − 2 x − 3 ( 1 x ) ′ = ( x − 1 2 ) ′ = − 1 2 x − 3 2 ( x ) ′ = ( x 1 2 ) ′ = 1 2 x − 1 2 = 1 2 x \\ \begin{aligned} &overhead:积分升幂(特例:\frac{1}{x})\\ &\int x^kdx=\frac{1}{k+1}x^{k+1}+C=\frac{x^p}{p}+C,p=k+1\\ &\int \frac{1}{x}dx=\int x^{-1}dx=ln|x|+C\\ &\int \frac{1}{x^2}dx=\int x^{-2}dx=-x^{-1}+C=-\frac{1}{x}+C\\ &\int \frac{1}{\sqrt{x}}dx=\int x^{-\frac{1}{2}}dx=2x^{\frac{1}{2}}+C=2\sqrt{x}+C\\ &\int \sqrt{x} dx=\int x^{\frac{1}{2}}dx=\frac{2}{3}x^{\frac{3}{2}}+C \end{aligned} \quad \large\begin{aligned} &overhead:求导降幂\\ &(x^k)'=kx^{k-1}\\ &(\frac{1}{x})'=(x^{-1})'=-x^{-2}=-\frac{1}{x^2}\\ &(\frac{1}{x^2})'=(x^{-2})'=-2x^{-3}\\ &(\frac{1}{\sqrt{x}})'=(x^{-\frac{1}{2}})'=-\frac{1}{2}x^{-\frac{3}{2}}\\ &(\sqrt{x})'=(x^{\frac{1}{2}})'=\frac{1}{2}x^{-\frac{1}{2}}=\frac{1}{2\sqrt{x}} \end{aligned} overhead:积分升幂(特例:x1)∫xkdx=k+11xk+1+C=pxp+C,p=k+1∫x1dx=∫x−1dx=ln∣x∣+C∫x21dx=∫x−2dx=−x−1+C=−x1+C∫x1dx=∫x−21dx=2x21+C=2x+C∫xdx=∫x21dx=32x23+Coverhead:求导降幂(xk)′=kxk−1(x1)′=(x−1)′=−x−2=−x21(x21)′=(x−2)′=−2x−3(x1)′=(x−21)′=−21x−23(x)′=(x21)′=21x−21=2x1
-
∫ x d x = 1 2 x 2 + c \int xdx=\frac{1}{2}x^2+c ∫xdx=21x2+c
-
∫ t a n x d x = ln ∣ s e c x ∣ + C \int tanxdx=\ln |secx|+C ∫tanxdx=ln∣secx∣+C
-
∫ c o t x d x = − ln ∣ c s c x ∣ + C = ln ∣ s i n x ∣ + C \int cotxdx=- \ln |cscx|+C=\ln |sinx|+C ∫cotxdx=−ln∣cscx∣+C=ln∣sinx∣+C
附:表格原码
-
由于某些markdown无法很好的从表格中的竖线
|区分开来,提供原码,可以用typora等渲染 -
| $f(x)$ | $f'(x)=\frac{d}{\mathrm{d}x}f(x)$ | $\displaystyle\int{f(x)}\mathrm{d}x$ | Note | | ----------------------------- | ------------------------------------------------- | ------------------------------------------------------------ | ----------------------------------- | | $k$ | 0 | $kx+C$ | | | $x^{\frac{1}{2}}=\sqrt{x}$ | $\frac{1}{2\sqrt{x}}=\frac{1}{2}x^{-\frac{1}{2}}$ | $\frac{2}{3}x^{\frac{3}{2}}+C$ | | | $\frac{1}{x}=x^{-1}$ | $-\frac{1}{x^2}=-x^{-2}$ | $\ln{|x|}+C$ | | | $x^{a}$ | $ax^{a-1}$ | $\frac{1}{a+1}x^{a+1}+C$ | $a\neq{-1}$ | | $a^x$ | $a^x\ln{a}$ | $\frac{1}{\ln{a}}a^x+C$ | $a>0, a\neq 1$ | | $e^x$ | $e^x$ | $e^x+C$ | | | $\log_a{x}$ | $\frac{1}{x\ln{a}}$ | $x\log_{a}x-\frac{1}{\ln{a}}x+C$ | 积分使用分部积分法 | | $\ln{x}$ | $\frac{1}{x}$ | $x\ln{x}-x+C$ | $(\ln|x|)'=\frac{1}{x}$ | | $\sin{x}$ | $\cos{x}$ | $-\cos{x}+C$ | | | $\cos{x}$ | $-\sin{x}$ | $\sin{x}+C$ | | | $\sec{x}$ | $\sec{x}\tan{x}$ | $\ln{|\sec{x}+\tan{x}|}+C$ | | | $\csc{x}$ | $-\csc{x}\cot{x}$ | $-\ln|\csc{x}+\cot{x}|+C=\ln|\csc{x}-\cot{x}|+C$ | NoteA | | $\tan{x}$ | $\sec^2{x}$ | $-\ln|\cos{x}|+C=\ln|\sec{x}|+C$ | | | $\cot{x}$ | $-\csc^2{x}$ | $\ln|\sin{x}|+C=-\ln|\csc{x}|+C$ | | | $\sin^2{x}$ | | $\frac{x}{2}-\frac{\sin{2x}}{4}+C$ | $\sin^2{x}=\frac{1}{2}(1-\cos{2x})$ | | $\cos^2{x}$ | | $\frac{x}{2}+\frac{\sin{2x}}{4}+C$ | $\cos^2{x}=\frac{1}{2}(1+\cos{2x})$ | | $\sec^2{x}$ | | $\tan{x}+C$ | | | $\csc^2{x}$ | | $-\cot{x}+C$ | | | $\tan^2{x}$ | | $\tan{x}-x+C$ | $\tan^2{x}=\sec^2x-1$ | | $\cot^2{x}$ | | $-\cot{x}-x+C$ | $\cot^2{x}=\csc^2{x}-1$ | | $\sec{x}\tan{x}$ | | $\sec{x}+C$ | | | $\csc{x}\cot{x}$ | | $-\csc{x}+C$ | | | $\arcsin{x}$ | $\frac{1}{\sqrt{1-x^2}}$ | | | | $\arccos{x}$ | $-\frac{1}{\sqrt{1-x^2}}$ | | | | $\arctan{x}$ | $\frac{1}{1+x^2}$ | | | | $\mathrm{arc}\cot{x}$ | $-\frac{1}{1+x^2}$ | | | | $\frac{1}{\sqrt{x^2\pm a^2}}$ | | $\ln|{x}+\sqrt{x^2\pm a^2}|+C$ | | | $\frac{1}{\sqrt{a^2-x^2}}$ | | $\arcsin{\frac{x}{a}}+C$ | | | $\frac{1}{\sqrt{1-x^2}}$ | | $\arcsin{x}+C$ | | | $\frac{1}{x^2+a^2}$ | | $\frac{1}{a}\arctan{\frac{x}{a}}+C$ | | | $\frac{1}{1+x^2}$ | | $\arctan{x}+C$ | | | $\frac{1}{x^2-a^2}$ | | $\frac{1}{2a}\ln|\frac{x-a}{x+a}|+C$ | | | $\sqrt{a^2-x^2}$ | | $\frac{1}{2}(a^2\arcsin{\frac{x}{a}}+x\sqrt{a^2-x^2})+C$ | $(a>|x|\geqslant{0})$ | | $\sqrt{x^2\pm{}a^2}$ | | $\frac{1}{2}(x\sqrt{x^2\pm{}a^2}\pm{}a^2\ln|x+\sqrt{x^2\pm{}a^2}|)$ | 参考数学分析(张) |



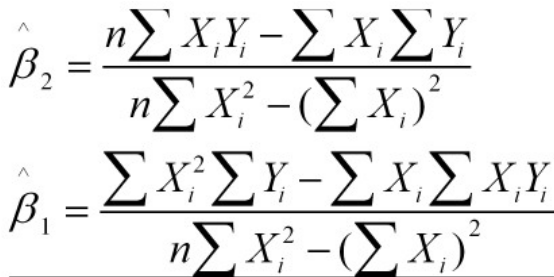

![[附源码]Nodejs计算机毕业设计基于社区疫情防控管理系统Express(程序+LW)](https://img-blog.csdnimg.cn/1498817b84be41ccbb699c3b260f7ae2.png)