🎆🎉🎉🎉🎉🎉🎉🎉🎉🎉🎉🎆
今天我要开启一个新计划----【C++天梯计划】
目的是通过天梯计划，通过题目和知识点串联的方式，完成C++复习与巩固。

什么是广搜?

宽度优先搜索算法（又称广度优先搜索）是最简便的图的搜索算法之一，这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。其别名又叫BFS，属于一种盲目搜寻法，目的是系统地展开并检查图中的所有节点，以找寻结果。换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。

与深搜的对比

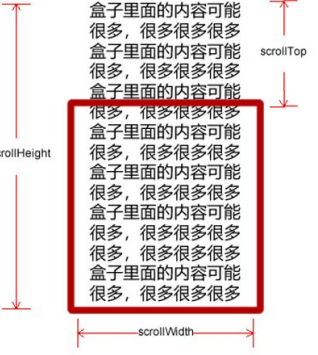
深度优先搜索用栈（stack）来实现，整个过程可以想象成一个倒立的树形：
1、 把根节点压入栈中。
2、 每次从栈中弹出一个元素，搜索所有在它下一级的元素，把这些元素压入栈中。并把这个元素记为它下一级元素的前驱。
3、 找到所要找的元素时结束程序。
4、 如果遍历整个树还没有找到，结束程序。
广度优先搜索使用队列（queue）来实现，整个过程也可以看做一个倒立的树形：
1、 把根节点放到队列的末尾。
2、 每次从队列的头部取出一个元素，查看这个元素所有的下一级元素，把它们放到队列的末尾。并把这个元素记为它下一级元素的前驱。
3、 找到所要找的元素时结束程序。
4、 如果遍历整个树还没有找到，结束程序。

实际应用

BFS在求解最短路径或者最短步数上有很多的应用。
应用最多的是在走迷宫上。
单独写代码有点泛化，取来自九度1335闯迷宫 [3] 一例说明，并给出C++/Java的具体实现。
在一个nn的矩阵里走，从原点（0,0）开始走到终点（n-1,n-1），只能上下左右4个方向走，只能在给定的矩阵里走，求最短步数。n*n是01矩阵，0代表该格子没有障碍，为1表示有障碍物。
int mazeArr[maxn][maxn]; //表示的是01矩阵
int stepArr[4][2] = {{-1,0},{1,0},{0,-1},{0,1}}; //表示上下左右4个方向
int visit[maxn][maxn]; //表示该点是否被访问过，防止回溯，回溯很耗时。
核心代码。基本上所有的BFS问题都可以使用类似的代码来解决。

例题1：快乐的马里奥

题目描述

马里奥是一个快乐的油漆工人，这天他接到了一个油漆任务，要求马里奥把一个 nn 行 mm 列的矩阵每一格都用油漆标记一个数字，标记的顺序按照广度优先搜索的方式进行，也就是他会按照如下方式标记：
1、首先标记第 11 行第 11 列的单元格，标记数字为 11 ；
2、然后标记当前单元格上下左右四个方向所有能标记的单元格，且：
① 标记顺序按照：右、下、左、上的优先级；
② 不能标到矩阵外，且标记过的数字不能重复标记；
3、当本单元格标记结束，寻找比本单元格中数字大 11 的单元格，标记那个单元格的上下左右四个方向，也是按照步骤 22 所示的要求进行标记。
依次类推，直到所有单元格都被标记。
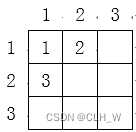
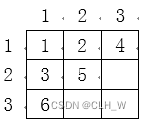
比如：如果有一个 3 \times 33×3 的矩阵如下，那么首先标记 1,11,1 单元格，并按照上面步骤 22 的要求标记其四周能够标记的单元格，标记结果如下：

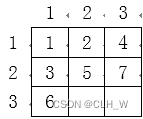
接下来，标记比 1,11,1 格大 11 的数字的四周的单元格，也就是标记值为 22 的单元格四周的单元格，标记结果如下：

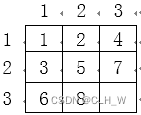
接下来标记值为 33 的单元格四周的单元格，标记结果如下：

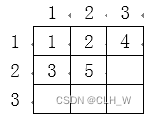
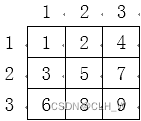
接下来标记值为 44 的单元格四周的单元格，标记结果如下：

接下来标记值为 55 的单元格四周的单元格，标记结果如下：

接下来标记值为 66 的单元格四周的单元格，但这个数字四周的单元格已经被标记，因此继续标记值为 77 四周的单元格，标记结果如下：

此时，发现标记结束，得到如上图所示的标记结果。

输入

两个整数 nn 和 mm （2 ＜ n,m ≤ 1002＜n,m≤100）。

输出

输出 nn 行 mm 列的标记后的矩阵，输出每个数后空一格。

样例

输入
3 3
输出
1 2 4
3 5 7
6 8 9

代码1

#include<bits/stdc++.h>
using namespace std;
//a存储矩阵
int a[110][110];
int n,m,i,j;
//方向数组 
int fx[5]={0,0,1,0,-1};
int fy[5]={0,1,0,-1,0};
queue<int> x, y; //坐标队列 
int s=1;
void bfs()
{
	x.push(1);
	y.push(1);
	a[1][1]=s;
	
	while(!x.empty())	
	{
		int tx=x.front(), ty=y.front();
		//以这一点为基础 找周边的点
		for(i=1; i<=4; i++)
		{
			int nx = tx + fx[i];
			int ny = ty + fy[i];
			if(nx>=1 && nx<=n && ny>=1 && ny<=m && a[nx][ny]==0)
			{
				s++;
				a[nx][ny]=s;
				x.push(nx);
				y.push(ny);
			}
		} 
		//基础点周边的点找完了 基础点出队列
		x.pop();
		y.pop(); 
	} 
}


int main()
{
	cin>>n>>m;
	bfs(); //广搜 
	
	for(int i = 1; i <= n; i++)
	{
		for( j = 1; j <= m; j++)
		{
			cout<< a[i][j] << " ";
		}
		cout << endl;
	}
}

代码2

#include<bits/stdc++.h>
using namespace std;

int a[110][110];//表示要存数的地图
int n,m;
int fx[5] = {0,0,1,0,-1};
int fy[5] = {0,1,0,-1,0}; 
int q[10010][3];//队列，存储每个访问过的点
int k = 1;//当前填到的数字 
int head,tail;//头尾指针 

int main(){
  	cin>>n>>m;
	//初始化
	head = 1;
	tail = 1; 
	
	//广搜：先存一个点，作为出发点
	q[1][1] = 1;
	q[1][2] = 1;
	a[1][1] = k;
	k++;
	 
	//当队列中有点可以访问时
	int tx,ty; 
	while(head <= tail){
		//查看队头可以去哪些点 
		//看队头的4个方向
		for(int i = 1;i <= 4;i++){
			//head对应点的坐标：q[head][1],q[head][2] 
			tx = q[head][1] + fx[i]; 
			ty = q[head][2] + fy[i];
			//如果这个点可以走：在迷宫内，没走过 
			if(tx>=1&&tx<=n&&ty>=1&&ty<=m&&a[tx][ty]==0){
				//走tx,ty点：将该点赋值，将该点存入队列 
				a[tx][ty] = k;
				k++;
				
				//将该点存入队列 
				tail++;
				q[tail][1] = tx;
				q[tail][2] = ty;
			} 
		}
		
		//当队头对应的4个方向的点都讨论完
		//让队头出队，讨论下一个点 
		head++;
	} 
	
	for(int i = 1;i <= n;i++){
		for(int j = 1;j <= m;j++){
			cout<<a[i][j]<<" ";
		}
		cout<<endl;
	}
    return 0; 
}

例题2：迷宫出口

题目描述

一天Extense在森林里探险的时候不小心走入了一个迷宫，迷宫可以看成是由 n \times nn×n 的格点组成，每个格点只有 22 种状态， 00 和 11，前者表示可以通行后者表示不能通行。
同时当Extense处在某个格点时，他只能移动到东南西北(或者说上下左右)四个方向之一的相邻格点上，Extense想要从点 AA 走到点 BB ，问在不走出迷宫的情况下能不能办到。
如果起点或者终点有一个不能通行(为 11)，则看成无法办到。

输入

第 11 行是一个正整数 nn (1 ≤ n ≤ 1001≤n≤100)，表示迷宫的规模是 n \times nn×n 的。
接下来是一个 n \times nn×n 的矩阵，矩阵中的元素为 00 或者 11。
再接下来一行是 44 个整数 haha lala hbhb lblb，描述 AA 处在第 haha 行 第 lala 列，BB 处在第 hbhb 行 第 lblb 列。

输出

能办到则输出“YES”，否则输出“NO”。

样例

输入
3
0 1 1
0 0 1
1 0 0
1 1 3 3
输出
YES

思路

从出发点开始，探测所有可探测的点，看是否有目标点，如果有，就表示可达，否
则表示不可达！
走到终点后，我们要将程序直接停掉，来避免不必要的递归：
（1）return：停止当前的函数，如果函数是递归产生的，不会停止所有的递归，只是停
止本次函数的递归，退到上一次调用的地方；
（2）exit(0)：停止程序，无论是否有递归，全部停止。

代码

#include <bits/stdc++.h>
using namespace std;
/*
1.判断如果起止点有1，就不能走；
2.从起点开始搜索，如果走到过终点，标记；
*/
int a[110][110];
int n;
int ha,la,hb,lb;
//搜索所有可行的点，走过标记
void dfs(int x,int y){
//cout<<x<<" "<<y<<endl;
a[x][y] = 1;//走过的点标记
//判断是否到达终点
if(x==hb&&y==lb){
cout<<"YES";
exit(0);
} 
//判断四个方向，是否有能走的点，如果有，直接递归执行
if(y+1<=n&&a[x][y+1]==0) dfs(x,y+1);
if(x+1<=n&&a[x+1][y]==0) dfs(x+1,y); 
if(y-1>=1&&a[x][y-1]==0) dfs(x,y-1);
if(x-1>=1&&a[x-1][y]==0) dfs(x-1,y);
} 
int main(){
cin>>n;
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
cin>>a[i][j];
}
} 
cin>>ha>>la>>hb>>lb;
//如果起止点不能走，输出NO
if(a[ha][la]==1 || a[hb][lb]==1){
cout<<"NO";
return 0;
} 
dfs(ha,la);//从ha,la开始搜索，走过的点标记为1 
cout<<"NO";
return 0;
}