集成学习方法之随机森林

1、集成学习方法

2、随机森林

3、随机森林原理

为什么采用BootStrap抽样

为什么要有放回地抽样

4、API

5、代码

代码解释

结果

6、随机森林总结

🍃作者介绍：双非本科大三网络工程专业在读，阿里云专家博主，专注于Java领域学习，擅长web应用开发、数据结构和算法，初步涉猎Python人工智能开发。

🦅主页：@逐梦苍穹

⭐分类算法系列①：初识概念

⭐分类算法系列②：KNN(K-近邻)算法

⭐分类算法系列③：模型选择与调优 (Facebook签到位置预测)

⭐分类算法系列④：朴素贝叶斯算法

⭐分类算法系列⑤：🎄决策树

🍁您的三连支持，是我创作的最大动力🌹

集成学习方法之随机森林

1、集成学习方法

集成学习通过建立几个模型组合的来解决单一预测问题。

它的工作原理是生成多个分类器/模型，各自独立地学习和作出预测。

这些预测最后结合成组合预测，因此优于任何一个单分类的做出预测。

集成学习方法（Ensemble Learning）是一种机器学习技术，旨在通过组合多个基本模型（弱学习器或基学习器）的预测来提高整体性能和泛化能力。集成学习的核心思想是，通过结合多个模型的意见和决策，可以减少单个模型的误差，并在各种不同情况下获得更稳健的结果。集成学习方法通常比单个模型更强大，适用于各种机器学习任务，包括分类、回归和聚类等。

以下是一些集成学习方法的主要概念和特点：

基本模型（弱学习器）： 集成学习通常由多个基本模型组成，这些基本模型可以是不同类型的机器学习算法，例如决策树、支持向量机、神经网络等。这些基本模型通常被称为弱学习器，它们不一定表现得非常强大，但它们应该略有不同。
组合策略： 集成学习方法使用一种组合策略来将多个基本模型的预测结果结合起来，以生成最终的集成模型的预测。常见的组合策略包括投票法、平均法、加权平均法等。组合策略的选择取决于任务的性质和问题的需求。
多样性： 集成学习的有效性依赖于基本模型之间的多样性。多样性意味着基本模型在不同方面或者在不同数据子集上产生不同的预测。多样性有助于减少模型的偏差，并提高整体性能。
Bagging和Boosting： Bagging（Bootstrap Aggregating）和Boosting是两种常见的集成学习方法。Bagging通过随机采样训练数据多次生成多个基本模型，并对它们的预测结果进行平均。Boosting则是通过迭代训练多个基本模型，每个模型都关注先前模型预测错误的样本，以便提高这些样本的分类准确度。
随机性： 随机性是集成学习中常用的技巧之一。通过引入随机性，例如随机抽样、随机特征选择等，可以增加模型的多样性，从而提高集成模型的性能。
特征重要性： 集成学习方法通常可以提供特征重要性的估计，帮助识别哪些特征对问题的解决起到了关键作用。

常见的集成学习方法包括随机森林（Random Forest）、AdaBoost、Gradient Boosting、XGBoost、LightGBM等。这些方法在各种机器学习竞赛和实际问题中都取得了显著的成功，因为它们可以显著提高模型的性能，减少过拟合，并提高泛化能力。集成学习方法是现代机器学习中的重要技术之一，广泛应用于各种领域。

2、随机森林

在机器学习中，随机森林是一个包含多个决策树的分类器，并且其输出的类别是由个别树输出的类别的众数而定。

例如, 如果你训练了5个树, 其中有4个树的结果是True, 1个数的结果是False, 那么最终投票结果就是True

随机森林(Random Forest)是一种集成学习方法，用于解决分类和回归问题。它基于决策树（Decision Tree）算法，通过构建多个决策树并将它们组合起来，从而提高了模型的性能和鲁棒性。以下是关于随机森林的主要特点和原理的解释：

集成方法： 随机森林是一种集成学习方法，意味着它将多个模型组合在一起，以获得比单个模型更好的性能。在随机森林中，这些模型是决策树，被称为森林中的树。
随机性： 随机森林引入了两种随机性来提高模型的多样性和鲁棒性。首先，它使用随机抽样技术从训练数据中随机选择一部分样本来训练每个决策树，这被称为自助采样（Bootstrap Sampling）。其次，在每次分裂节点时，它随机选择一个子集的特征来进行分裂，而不是考虑所有特征。这种随机性有助于减少模型的过拟合问题。
多个决策树： 随机森林通常由多个决策树组成，每个决策树都独立地训练，并且每个树都对数据进行不同的采样和特征选择。这些决策树之间是相互独立的，它们的预测结果会被组合起来。
投票或平均： 在分类问题中，随机森林通常采用多数投票的方式来确定最终的分类结果。也就是说，每个决策树都对输入样本进行分类，最终分类结果是得到最多投票的类别。在回归问题中，随机森林采用平均的方式，将每个决策树的预测结果取平均值作为最终的预测值。
高性能和鲁棒性： 随机森林具有良好的性能和鲁棒性。它通常对异常值和噪声具有一定的容忍度，并且不太容易过拟合。由于多个决策树的组合，随机森林通常能够捕获数据中的复杂关系，从而在各种问题上表现良好。
特征重要性： 随机森林可以估计每个特征的重要性，以帮助了解哪些特征对问题的解决具有更大的影响力。

总之，随机森林是一种强大的机器学习方法，适用于多种任务，包括分类和回归。它通过引入随机性、构建多个决策树并将它们组合起来，提供了高性能、鲁棒性和泛化能力强的模型。这使得它成为许多实际问题中的首选算法之一。

3、随机森林原理

随机森林的数学原理涉及到随机抽样、特征选择、决策树构建和集成方法。

以下是更详细的数学公式和说明：

1. 随机抽样（Bootstrap Sampling）：

随机森林使用Bootstrap采样从训练数据集中随机选择N个样本，其中N是训练数据集的大小。

这个过程可以用以下数学公式表示：

给定训练数据集D，包含N个样本： $D = \{ (x_1, y_1), (x_2, y_2), ..., (x_N, y_N) \}$
随机抽样生成一个自助采样集D'，包含N个样本，每个样本通过有放回的方式抽取： $D' = \{ (x_i, y_i) \}, i \in \{1, 2, ..., N\}$

这个过程引入了数据的随机性，使得每棵决策树的训练数据都略有不同。

2. 特征随机选择：

在每次决策树节点的分裂过程中，随机森林引入了特征的随机性。

假设总共有M个特征，在每次分裂节点时，从这些特征中随机选择m个特征，其中m通常由用户指定。

这可以表示为以下数学公式：

$A \subset M, \ |A| = m$
给定总特征数M和每次分裂所选特征数m，随机选择一个特征子集A，其中A包含m个特征，A是M中的子集。

3. 决策树的构建：

决策树的构建过程涉及到选择最佳特征和分裂点，通常通过一些分裂标准（例如信息增益、基尼指数）来确定。具体的数学公式和说明可能因使用的决策树算法而异。

4. 集成方法：

在随机森林中，多个决策树的结果被集成以进行分类或回归。对于分类问题，最终的分类结果是通过多数投票法来确定：

给定N个决策树的分类结果 $C_1, C_2, ..., C_N$ ，其中每个 $C_i$ 是一个类别。
最终的分类结果 $C_{final}$ 是获得最多投票的类别。

对于回归问题，最终的回归结果是多个决策树的预测结果的平均值：

给定N个决策树的回归结果 $R_1,R_2,...,R_N$ ，其中每个 $R_i$ 是一个实数值。
最终的回归结果 $R_{final}$ 是 $R_{final} = \frac{1}{N} \sum_{i=1}^{N} R_i$

这个过程将多个模型的预测结果合并为一个最终的预测结果。

5. 特征重要性评估：

随机森林通常通过观察每个特征在多个决策树中的分裂情况以及其对模型性能的影响来估计特征的重要性。一个常用的方法是通过特征在决策树中用于分裂的次数来评估其重要性，次数越多，特征越重要。

需要注意的是，具体的数学公式和算法细节可能因随机森林的实现和问题的不同而有所不同。上述内容提供了随机森林数学原理的一般概述，具体的数学公式和推导可能需要进一步深入研究和了解随机森林的具体实现。

为什么采用BootStrap抽样

随机森林采用Bootstrap抽样的主要原因是为了引入数据的随机性和多样性，从而提高模型的性能和泛化能力。下面是为什么采用Bootstrap抽样的几个关键原因：

引入随机性： Bootstrap抽样是一种有放回的随机抽样方法，它允许相同的样本被多次抽取，同时可能导致某些样本被排除。这种随机性使得每个Bootstrap样本都是从原始数据中随机选择的，从而引入了数据的随机性。
增加多样性： 由于每个Bootstrap样本都是略有不同的，每棵决策树的训练数据也会有所不同。这增加了每个决策树的多样性，因为它们基于不同的训练数据进行训练。多样性有助于减少过拟合，提高模型的泛化能力。
降低方差： 随机森林的核心思想之一是通过组合多个决策树的结果来降低模型的方差。由于每个决策树都是在不同的Bootstrap样本上训练的，它们会产生不同的预测结果。通过取多个决策树的平均值或多数投票，可以降低单个决策树的方差，从而提高模型的稳定性。
增加模型的鲁棒性： 由于Bootstrap抽样引入了数据的随机性，模型对于训练数据中的噪声和异常值具有一定的鲁棒性。这意味着随机森林对于一些数据中的不确定性能够更好地处理。

总的来说，采用Bootstrap抽样是随机森林成功的关键因素之一，它通过引入随机性、多样性和降低方差的方式改善了模型的性能，使其在各种问题中表现出色。这种随机性和多样性是随机森林的特点，使其成为强大的集成学习方法。

为什么要有放回地抽样

如果不是有放回的抽样，那么每棵树的训练样本都是不同的，都是没有交集的，这样每棵树训练出来都是有很大的差异的；

而随机森林最后分类取决于多棵树（弱分类器）的投票表决。

4、API

class sklearn.ensemble.RandomForestClassifier(

        n_estimators=10, criterion=’gini’, max_depth=None, bootstrap=True, random_state=None, min_samples_split=2)

    随机森林分类器

    n_estimators：integer，optional（default = 10）森林里的树木数量120,200,300,500,800,1200

    criteria：string，可选（default =“gini”）分割特征的测量方法

    max_depth：integer或None，可选（默认=无）树的最大深度 5,8,15,25,30

    max_features="auto”,每个决策树的最大特征数量

    If "auto", then max_features=sqrt(n_features).

    If "sqrt", then max_features=sqrt(n_features) (same as "auto").

    If "log2", then max_features=log2(n_features).

    If None, then max_features=n_features.

    bootstrap：boolean，optional（default = True）是否在构建树时使用放回抽样

    min_samples_split:节点划分最少样本数

    min_samples_leaf:叶子节点的最小样本数

    超参数：n_estimator, max_depth, min_samples_split,min_samples_leaf

5、代码

# -*- coding: utf-8 -*-
# @Author:︶ㄣ释然
# @Time: 2023/9/2 23:07
import pandas as pd
from sklearn.ensemble import RandomForestClassifier
from sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import train_test_split, GridSearchCV

'''
class sklearn.ensemble.RandomForestClassifier(
        n_estimators=10, criterion=’gini’, max_depth=None, bootstrap=True, random_state=None, min_samples_split=2)
    随机森林分类器
    n_estimators：integer，optional（default = 10）森林里的树木数量120,200,300,500,800,1200
    criteria：string，可选（default =“gini”）分割特征的测量方法
    max_depth：integer或None，可选（默认=无）树的最大深度 5,8,15,25,30
    max_features="auto”,每个决策树的最大特征数量
    If "auto", then max_features=sqrt(n_features).
    If "sqrt", then max_features=sqrt(n_features) (same as "auto").
    If "log2", then max_features=log2(n_features).
    If None, then max_features=n_features.
    bootstrap：boolean，optional（default = True）是否在构建树时使用放回抽样
    min_samples_split:节点划分最少样本数
    min_samples_leaf:叶子节点的最小样本数
    超参数：n_estimator, max_depth, min_samples_split,min_samples_leaf
'''
def randomForest():
    """
        决策树进行乘客生存预测
        """
    # 1、获取数据
    titan = pd.read_csv("./data/titanic/titanic.csv")

    # 2、数据的处理
    x = titan[['pclass', 'age', 'sex']]

    y = titan['survived']

    # print(x , y)
    # 缺失值需要处理，将特征当中有类别的这些特征进行字典特征抽取
    x['age'].fillna(x['age'].mean(), inplace=True)

    # 对于x转换成字典数据x.to_dict(orient="records")
    # [{"pclass": "1st", "age": 29.00, "sex": "female"}, {}]

    dict = DictVectorizer(sparse=False)

    x = dict.fit_transform(x.to_dict(orient="records"))

    print(dict.get_feature_names_out())
    print(x)

    # 分割训练集合测试集
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3)

    # 在决策树代码中，下面开始使用决策树预估器
    # 这里需要使用的是随机森林，先引入网格搜索与交叉验证
    # 引入随机森林分类器
    estimator = RandomForestClassifier()
    # 加入网格搜索与交叉验证
    # 参数准备
    param_dict = {"n_estimators": [120, 200, 300, 500, 800, 1200], "max_depth": [5, 8, 15, 25, 30]}
    estimator = GridSearchCV(estimator, param_grid=param_dict, cv=3)
    estimator.fit(x_train, y_train)

    # 5）模型评估
    # 方法1：直接比对真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\n", y_predict)
    print("直接比对真实值和预测值:\n", y_test == y_predict)

    # 方法2：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：\n", score)

    # 最佳参数：best_params_
    print("最佳参数：\n", estimator.best_params_)
    # 最佳结果：best_score_
    print("最佳结果：\n", estimator.best_score_)
    # 最佳估计器：best_estimator_
    print("最佳估计器:\n", estimator.best_estimator_)
    # 交叉验证结果：cv_results_
    print("交叉验证结果:\n", estimator.cv_results_)


if __name__ == '__main__':
    randomForest()

代码解释

这段代码的主要目标是使用随机森林（RandomForestClassifier）来建立一个生存预测模型，该模型用于预测泰坦尼克号乘客的生存情况。以下是代码的主要步骤和功能：

导入必要的库和模块，包括pandas用于数据处理，sklearn中的随机森林分类器（RandomForestClassifier）、字典特征抽取（DictVectorizer）以及网格搜索与交叉验证（GridSearchCV）。
从CSV文件中加载泰坦尼克号乘客的数据集，将数据存储在名为 "titan" 的DataFrame中。
数据预处理：
- 选择特征：从数据集中选择了三个特征，包括 'pclass'（船舱等级）、'age'（年龄）、'sex'（性别）。
- 处理缺失值：对 'age' 特征中的缺失值使用平均值进行填充。
- 字典特征抽取：使用DictVectorizer将选择的特征转换为字典数据表示。
分割训练集和测试集：将数据集划分为训练集（x_train, y_train）和测试集（x_test, y_test），其中x包含特征，y包含目标（生存情况）。
创建随机森林模型：
- 定义一个随机森林分类器（RandomForestClassifier）的实例。
- 使用网格搜索与交叉验证（GridSearchCV）来搜索最佳超参数，包括 'n_estimators'（决策树的数量）和 'max_depth'（决策树的最大深度）。
模型训练：使用训练集（x_train, y_train）训练随机森林分类器，找到最佳超参数组合。
模型评估：
- 使用训练好的模型进行预测（y_predict）。
- 比对预测值和真实值，输出比对结果。
- 计算模型的准确率（score）来评估模型性能。
- 打印出最佳参数（best_params_）、最佳结果（best_score_）、最佳估计器（best_estimator_）以及交叉验证结果（cv_results_）。

总之，这段代码使用了随机森林算法来构建一个生存预测模型，通过网格搜索和交叉验证选择最佳超参数，然后对模型进行训练和评估，最终输出了模型的性能指标和最佳参数。这个模型可用于预测泰坦尼克号乘客是否生存。

结果

部分结果：

全部结果：

['age' 'pclass=1st' 'pclass=2nd' 'pclass=3rd' 'sex=female' 'sex=male']
[[29.          1.          0.          0.          1.          0.        ]
 [ 2.          1.          0.          0.          1.          0.        ]
 [30.          1.          0.          0.          0.          1.        ]
 ...
 [31.19418104  0.          0.          1.          0.          1.        ]
 [31.19418104  0.          0.          1.          1.          0.        ]
 [31.19418104  0.          0.          1.          0.          1.        ]]
y_predict:
 [0 1 0 0 1 0 0 0 0 1 1 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0 0 1 1
 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0
 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
 0 0 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0
 1 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0
 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 1 1 0 1 1 0 0 1 0 0 1 0 1 0 0 0 1 1 0 0 1
 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0
 0 0 1 0 0 1 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0
 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 0 0 0 0 0 0 0 1 1 0 0 0 1
 1 0 0 0 1 1 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0]
直接比对真实值和预测值:
 372      True
331      True
419      True
1207    False
214      True
        ...  
353      True
638      True
1206     True
837      True
150     False
Name: survived, Length: 394, dtype: bool
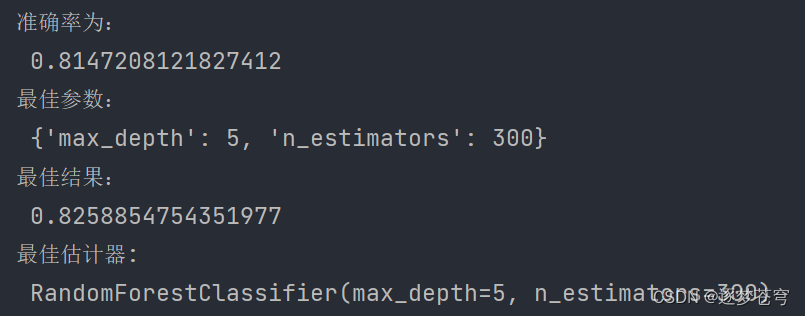
准确率为：
 0.8147208121827412
最佳参数：
 {'max_depth': 5, 'n_estimators': 300}
最佳结果：
 0.8258854754351977
最佳估计器:
 RandomForestClassifier(max_depth=5, n_estimators=300)
交叉验证结果:
 {'mean_fit_time': array([0.34114035, 0.6787285 , 1.19496473, 1.63294808, 2.61791738,
       3.90683413, 0.42621287, 0.66980179, 1.045005  , 1.74056196,
       2.94625727, 4.13277896, 0.42489568, 0.72270465, 1.04371158,
       1.64689604, 2.64780331, 4.51028919, 0.36052966, 0.71541214,
       1.28693382, 2.07006788, 2.96712073, 4.48969253, 0.51682838,
       0.78613575, 1.24840148, 1.92716988, 2.94232289, 4.1270256 ]), 'std_fit_time': array([0.02160469, 0.06343764, 0.15187076, 0.03610656, 0.16918523,
       0.33522165, 0.00201884, 0.04676447, 0.02417938, 0.11845516,
       0.19509487, 0.23404712, 0.03392946, 0.07600673, 0.10253338,
       0.09753914, 0.09068534, 0.30426279, 0.01880941, 0.17041238,
       0.16278968, 0.02310135, 0.19769377, 0.17910675, 0.04927973,
       0.04468589, 0.21264184, 0.13745615, 0.21043222, 0.13223121]), 'mean_score_time': array([0.02984413, 0.06995718, 0.10653249, 0.13419573, 0.30652507,
       0.31377006, 0.03470572, 0.05790703, 0.09903876, 0.15190991,
       0.22437676, 0.36459335, 0.03852383, 0.06104024, 0.08556557,
       0.1638821 , 0.22833014, 0.44704652, 0.03534373, 0.07807342,
       0.14058359, 0.1698943 , 0.22634244, 0.46184222, 0.04569523,
       0.07974943, 0.1173528 , 0.1592354 , 0.27193197, 0.33379459]), 'std_score_time': array([0.00183949, 0.00774793, 0.01441184, 0.01287631, 0.10014877,
       0.01743236, 0.00193149, 0.00898091, 0.01622788, 0.00807192,
       0.01109652, 0.04542851, 0.00246657, 0.00328897, 0.00780091,
       0.02189977, 0.0185611 , 0.1126361 , 0.00214615, 0.03355603,
       0.047558  , 0.03386113, 0.01724394, 0.0909068 , 0.00655658,
       0.0122869 , 0.01489499, 0.00573899, 0.022459  , 0.01732852]), 'param_max_depth': masked_array(data=[5, 5, 5, 5, 5, 5, 8, 8, 8, 8, 8, 8, 15, 15, 15, 15, 15,
                   15, 25, 25, 25, 25, 25, 25, 30, 30, 30, 30, 30, 30],
             mask=[False, False, False, False, False, False, False, False,
                   False, False, False, False, False, False, False, False,
                   False, False, False, False, False, False, False, False,
                   False, False, False, False, False, False],
       fill_value='?',
            dtype=object), 'param_n_estimators': masked_array(data=[120, 200, 300, 500, 800, 1200, 120, 200, 300, 500, 800,
                   1200, 120, 200, 300, 500, 800, 1200, 120, 200, 300,
                   500, 800, 1200, 120, 200, 300, 500, 800, 1200],
             mask=[False, False, False, False, False, False, False, False,
                   False, False, False, False, False, False, False, False,
                   False, False, False, False, False, False, False, False,
                   False, False, False, False, False, False],
       fill_value='?',
            dtype=object), 'params': [{'max_depth': 5, 'n_estimators': 120}, {'max_depth': 5, 'n_estimators': 200}, {'max_depth': 5, 'n_estimators': 300}, {'max_depth': 5, 'n_estimators': 500}, {'max_depth': 5, 'n_estimators': 800}, {'max_depth': 5, 'n_estimators': 1200}, {'max_depth': 8, 'n_estimators': 120}, {'max_depth': 8, 'n_estimators': 200}, {'max_depth': 8, 'n_estimators': 300}, {'max_depth': 8, 'n_estimators': 500}, {'max_depth': 8, 'n_estimators': 800}, {'max_depth': 8, 'n_estimators': 1200}, {'max_depth': 15, 'n_estimators': 120}, {'max_depth': 15, 'n_estimators': 200}, {'max_depth': 15, 'n_estimators': 300}, {'max_depth': 15, 'n_estimators': 500}, {'max_depth': 15, 'n_estimators': 800}, {'max_depth': 15, 'n_estimators': 1200}, {'max_depth': 25, 'n_estimators': 120}, {'max_depth': 25, 'n_estimators': 200}, {'max_depth': 25, 'n_estimators': 300}, {'max_depth': 25, 'n_estimators': 500}, {'max_depth': 25, 'n_estimators': 800}, {'max_depth': 25, 'n_estimators': 1200}, {'max_depth': 30, 'n_estimators': 120}, {'max_depth': 30, 'n_estimators': 200}, {'max_depth': 30, 'n_estimators': 300}, {'max_depth': 30, 'n_estimators': 500}, {'max_depth': 30, 'n_estimators': 800}, {'max_depth': 30, 'n_estimators': 1200}], 'split0_test_score': array([0.83713355, 0.83713355, 0.83713355, 0.83713355, 0.83713355,
       0.83713355, 0.81107492, 0.81758958, 0.83061889, 0.81433225,
       0.81758958, 0.81107492, 0.80781759, 0.80456026, 0.81107492,
       0.81433225, 0.80781759, 0.80781759, 0.81107492, 0.81107492,
       0.81107492, 0.80781759, 0.80781759, 0.81107492, 0.81107492,
       0.81107492, 0.81107492, 0.81107492, 0.81107492, 0.81107492]), 'split1_test_score': array([0.83333333, 0.83006536, 0.83333333, 0.83006536, 0.83333333,
       0.83333333, 0.81372549, 0.81699346, 0.81699346, 0.81699346,
       0.81699346, 0.81699346, 0.81372549, 0.81699346, 0.81699346,
       0.81699346, 0.81699346, 0.81699346, 0.81699346, 0.81699346,
       0.80718954, 0.81372549, 0.81699346, 0.81699346, 0.81699346,
       0.81699346, 0.81699346, 0.81699346, 0.81699346, 0.81699346]), 'split2_test_score': array([0.79738562, 0.79738562, 0.80718954, 0.79738562, 0.79738562,
       0.80392157, 0.79738562, 0.79738562, 0.79738562, 0.79738562,
       0.79738562, 0.79738562, 0.79738562, 0.79738562, 0.80065359,
       0.80065359, 0.80065359, 0.79411765, 0.80065359, 0.79738562,
       0.79411765, 0.79411765, 0.80065359, 0.80065359, 0.80065359,
       0.80065359, 0.79738562, 0.79411765, 0.79738562, 0.79738562]), 'mean_test_score': array([0.8226175 , 0.82152818, 0.82588548, 0.82152818, 0.8226175 ,
       0.82479615, 0.80739534, 0.81065622, 0.81499933, 0.80957044,
       0.81065622, 0.80848467, 0.80630957, 0.80631312, 0.80957399,
       0.81065977, 0.80848822, 0.80630957, 0.80957399, 0.80848467,
       0.80412737, 0.80522024, 0.80848822, 0.80957399, 0.80957399,
       0.80957399, 0.80848467, 0.80739534, 0.80848467, 0.80848467]), 'std_test_score': array([0.01790896, 0.01731352, 0.01331074, 0.01731352, 0.01790896,
       0.01484187, 0.00716018, 0.00938689, 0.0136405 , 0.0086842 ,
       0.00938689, 0.00821174, 0.00675541, 0.00810026, 0.00675462,
       0.00715836, 0.00668756, 0.00939969, 0.00675462, 0.00821174,
       0.0072535 , 0.00821286, 0.00668756, 0.00675462, 0.00675462,
       0.00675462, 0.00821174, 0.00969468, 0.00821174, 0.00821174]), 'rank_test_score': array([ 3,  5,  1,  5,  3,  2, 24,  9,  7, 16,  9, 19, 27, 26, 11,  8, 17,
       27, 11, 19, 30, 29, 17, 11, 11, 11, 19, 25, 19, 19])}

保存为文件(复制到浏览器访问即可自动下载到本地)：

随机森林验证泰坦尼克号运行结果.txt