本章代码gitee仓库:排序
文章目录
- 🎃0. 思维导图
- 🧨1. 插入排序
- ✨1.1 直接插入排序
- ✨1.2 希尔排序
- 🎊2. 选择排序
- 🎋2.1 直接选择排序
- 🎋2.2 堆排序
- 🎏3. 交换排序
- 🎐3.1 冒泡排序
- 🎐3.2 快速排序
- 🎑hoare版本
- 🎑挖坑法
- 🎑前后指针
- 🎑小区间优化
- 🎑非递归
- 🎀4. 归并排序
- 🎁4.1 递归
- 🎁4.2 非递归
- 🎫5. 性能测试
- 🎖5.1 1w数据
- 🎖5.2 10w数据
- 🎖5.3 100w数据
- 🎖5.4 1000w数据
- 🎖5.5 1亿数据
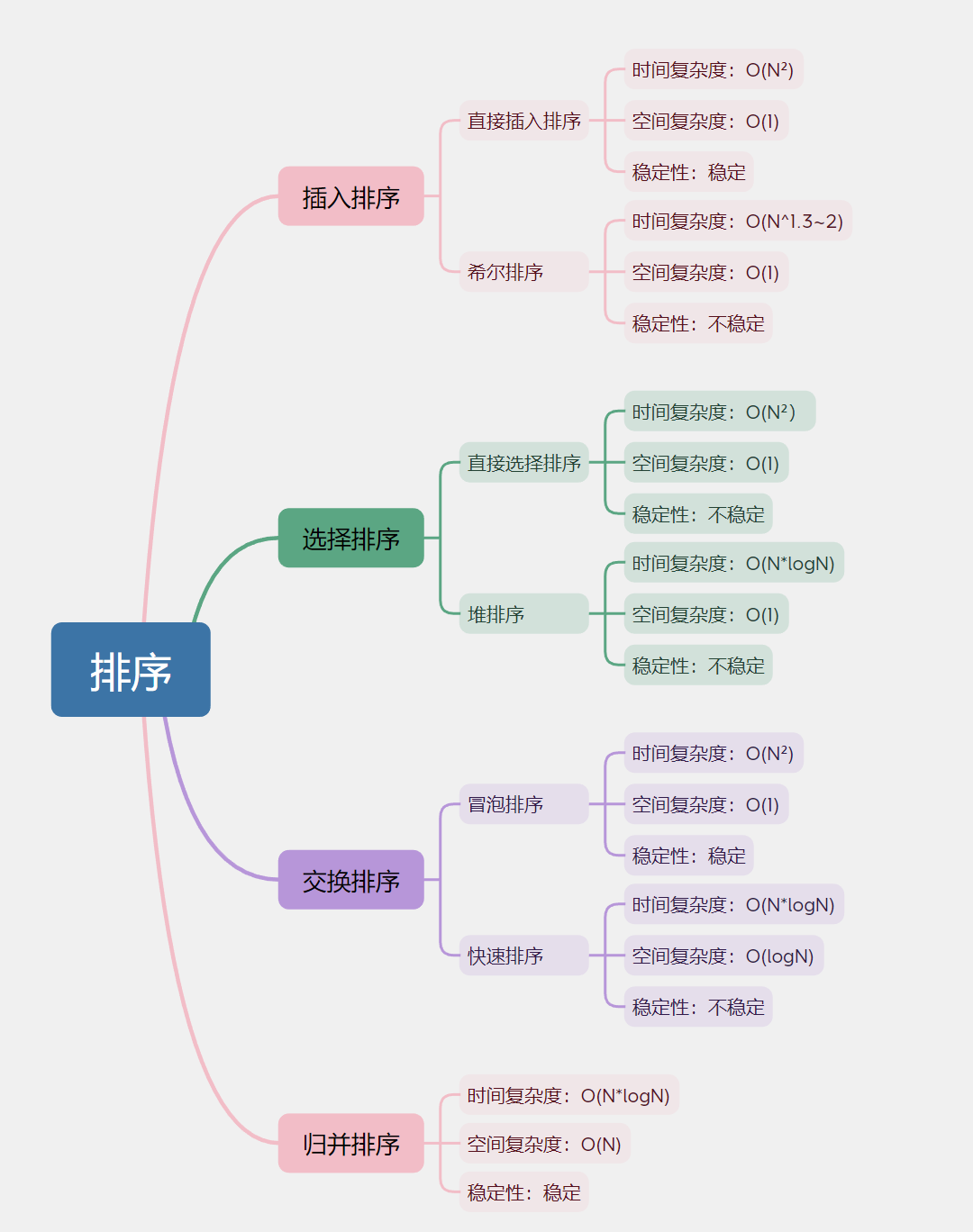
🎃0. 思维导图
🧨1. 插入排序
✨1.1 直接插入排序
我们日常打扑克牌,摸牌,让后将牌按顺序插入好,这其实就是插入排序的过程,打小插入排序的思想就植入我们的脑海
第一张牌不用管,直接拿在手里,之后的牌按照大小再一个一个插入即可
//直接插入排序
void InsertSort(int* a, int n)
{
//第一张牌不用排,所以直接从下标1开始走
for (int i = 1; i < n; i++)
{
int end = i - 1;
int tmp = a[i];
while (end >= 0)
{
if (a[end] > tmp)
{
//往后挪数据
a[end + 1] = a[end];
end--;
}
else
break;
}
//直接break出来 或者 end = -1
a[end + 1] = tmp;
}
}
直接插入排序特性:
越接近有序,效率越高(不用那么多次挪动数据)
时间复杂度:O(N2)
逆序最坏O(N2),有序最好O(N)
空间复杂度:O(1)
稳定性:稳定
✨1.2 希尔排序
希尔排序是基于直接插入排序的一种优化,将数据分为gap组,对每组进行排序,然后再缩小间隔,知道gap为1的时候,该序列为有序
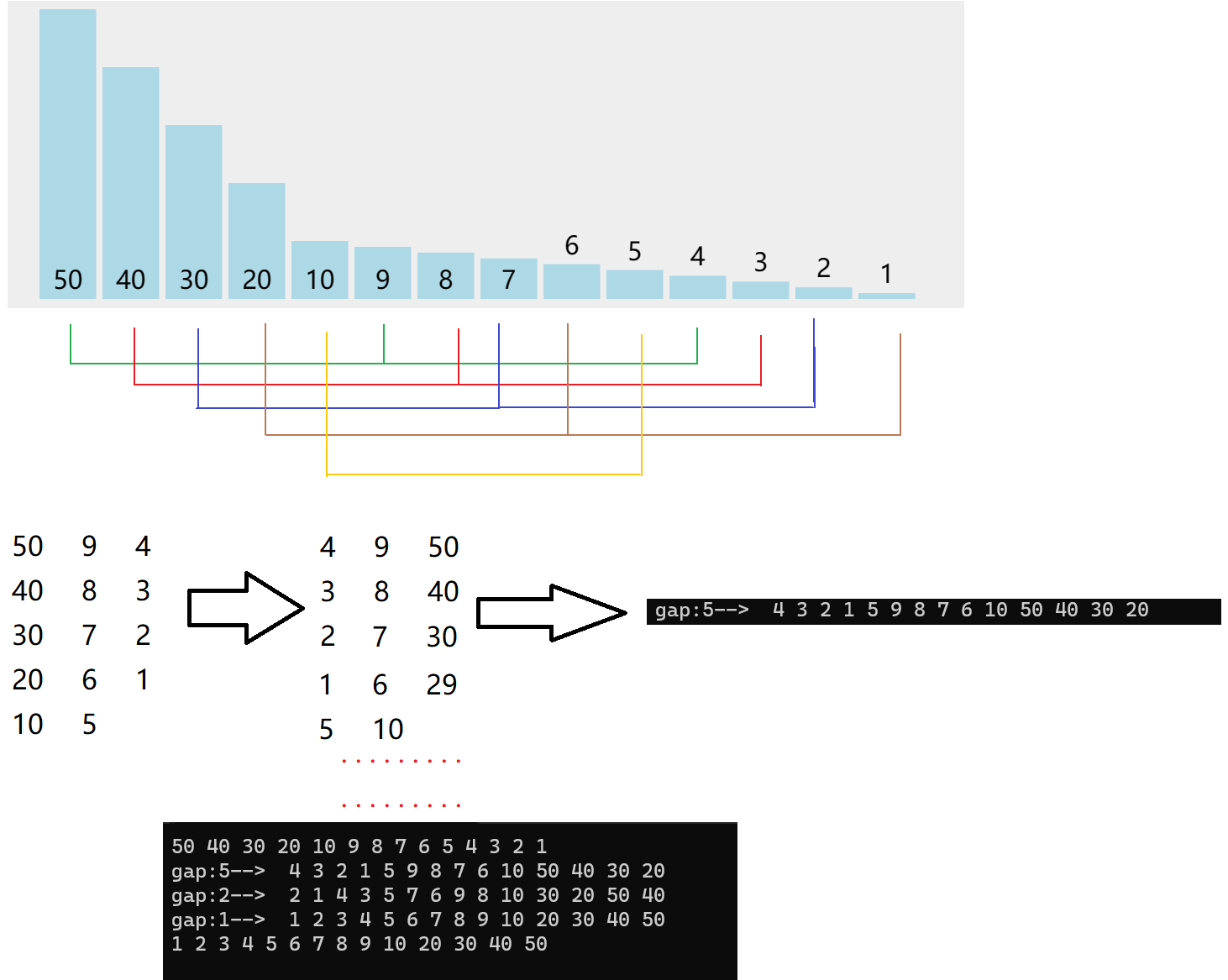
//希尔排序
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
//最后一次gap一定要是1
gap = gap / 3 + 1;
//分组插入排序 预排序
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[i + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
else
break;
}
a[end + gap] = tmp;
}
}
}
希尔排序特性:
希尔排序有2层循环,一个是
gap的逐渐缩小,一个是分为gap组之后的插入排序,我们一般以为时间复杂度为**O(N*logN)**这个量级。但其实这其中的N,一直是在变化的,可理解为先上升,后下降
所以这个量级是略大于N*logN,查阅资料可得知,希尔排序的时间复杂度大概为O(N1.3~2)
稳定性:不稳定
🎊2. 选择排序
还是以打扑克来举例,有时候我们感觉一张一张摸牌十分费时间,所以就指定一个人来发牌,发完之后我们将这一把牌拿到手中再开始理牌
🎋2.1 直接选择排序
这个选择排序每次都是趟都是选出最小的数,我们可以在此基础上做出优化,每次选出2个数,即最小值和最大值
//选择排序
void SelectSort(int* a, int n)
{
int left = 0;
int right = n - 1;
while (left < right)
{
int mini = left;
int maxi = left;
for (int i = left + 1; i <= right; i++)
{
if (a[i] < a[mini])
{
mini = i;
}
if (a[i] > a[maxi])
{
maxi = i;
}
}
Swap(&a[left], &a[mini]);
//数据修正
if (a[left] == a[maxi])
{
maxi = mini;
}
Swap(&a[right], &a[maxi]);
left++;
right--;
}
}
直接选择排序特性:
不考虑序列的有序性,每次都找出最小最大值,效率较低
时间复杂度:O(N2)
最好情况:O(N2)
最坏情况:O(N2)
空间复杂度:O(1)
稳定性:不稳定
🎋2.2 堆排序
堆排序也是选择排序的一种,只不过没有直接选择排序那么朴实,堆排序有一些“华丽”的技巧。
堆排序在之前二叉树的章节讲过了,这里就不再过多赘述,有兴趣的可以查看此篇文章:数据结构——二叉树
//向下调整 前提:子树都是堆
void AdjustDown(int* val, int sz, int parent)
{
//默认左孩子大
int child = parent * 2 + 1;
//至多叶子结点结束
while (child < sz)
{
//不越界 选出更大的孩子
if (child + 1 < sz && val[child] < val[child + 1])
{
child++;
}
if (val[child] > val[parent])
{
Swap(&val[child], &val[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//堆排序
void HeapSort(int* a, int n)
{
//向下调整 O(N)
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDown(a,n, i);
}
//向下调整排序 O(N*logN)
for (int i = 0; i < n; i++)
{
Swap(&a[0], &a[n - 1 - i]);
AdjustDown(a, n - 1 - i, 0);
}
}
堆排序特性:
- 堆排序进行选数据效率较高
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
🎏3. 交换排序
🎐3.1 冒泡排序
冒泡排序应该是多数人的启蒙排序算法,思路较为简单
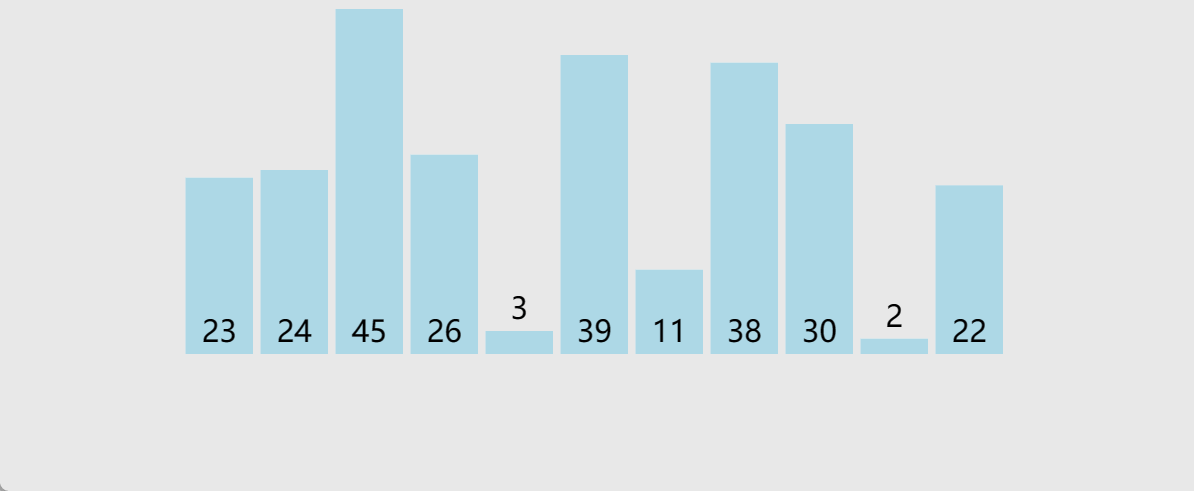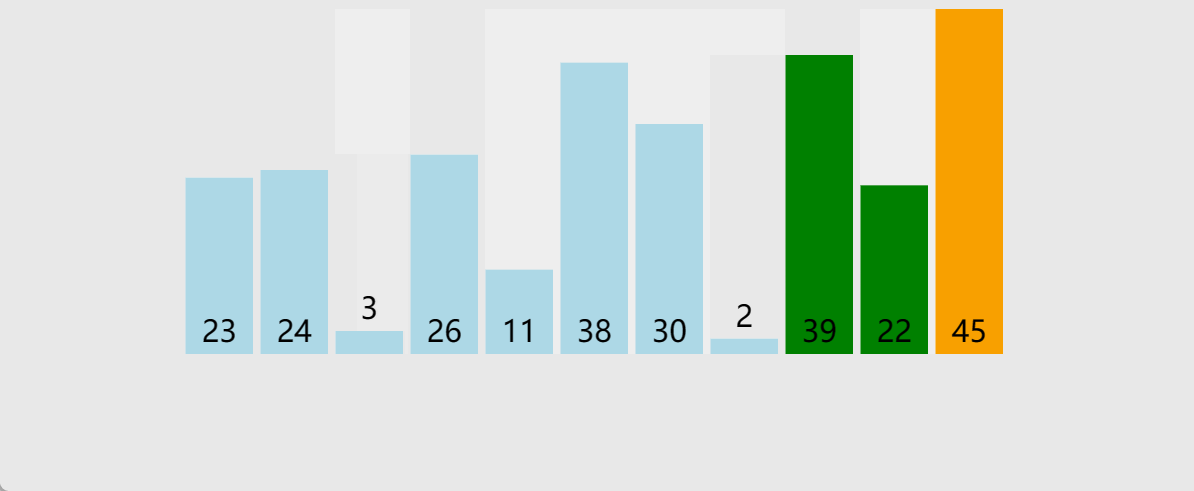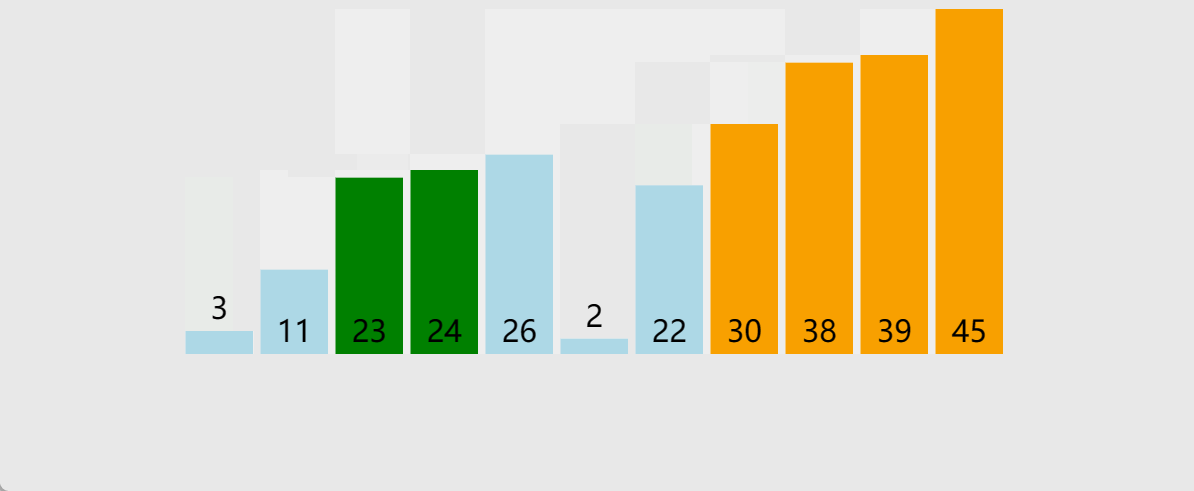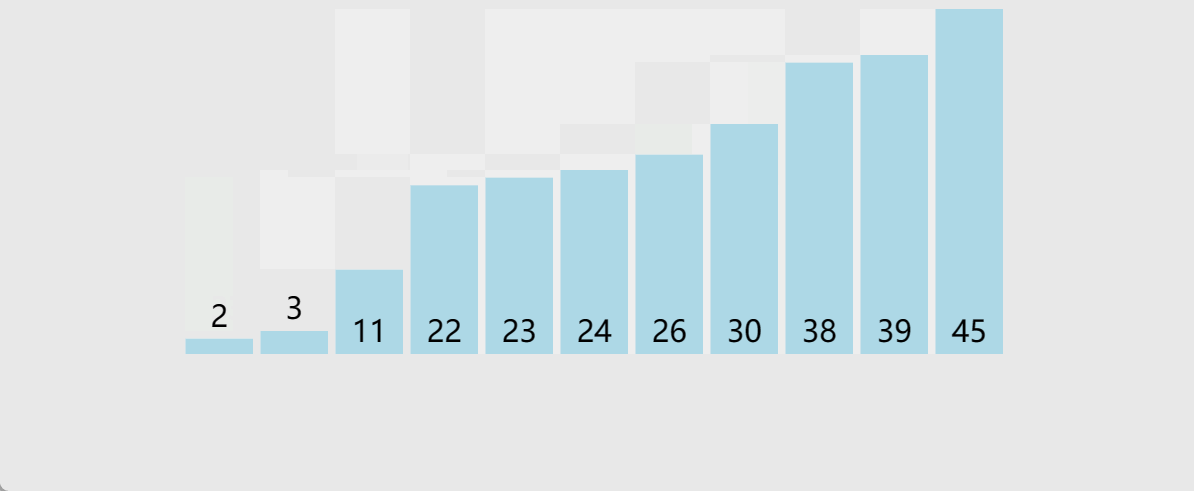
//冒泡排序
void BubbleSort(int* a, int n)
{
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n - i - 1; j++)
{
if (a[j] > a[j + 1])
{
Swap(&a[j], &a[j + 1]);
}
}
}
}
冒泡排序特性:
时间复杂度:O(N2)
最坏情况:O(N2)
最好情况:O(N)
空间复杂度:O(1)
稳定性:稳定
这里的最好情况,就是里面没有发送交换了,就证明此时序列已经有序,则不需要往后再遍历,优化如下:
//冒泡排序
void BubbleSort(int* a, int n)
{
for (int i = 0; i < n; i++)
{
bool falg = true;
for (int j = 0; j < n - i - 1; j++)
{
if (a[j] > a[j + 1])
{
Swap(&a[j], &a[j + 1]);
falg = false;
}
}
if (falg)
break;
}
}
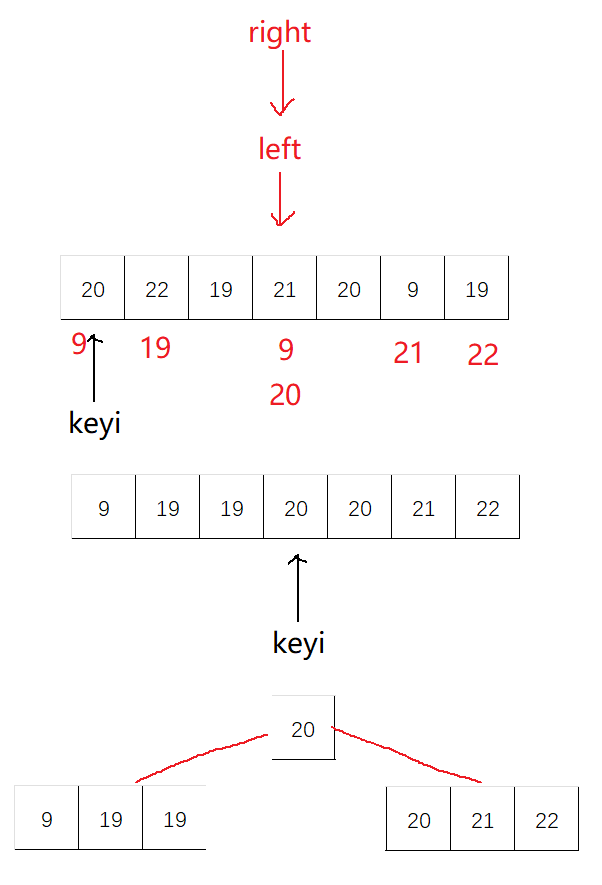
🎐3.2 快速排序
快速排序,顾名思义,速度很快,效率很高,排序算法里面的大哥大
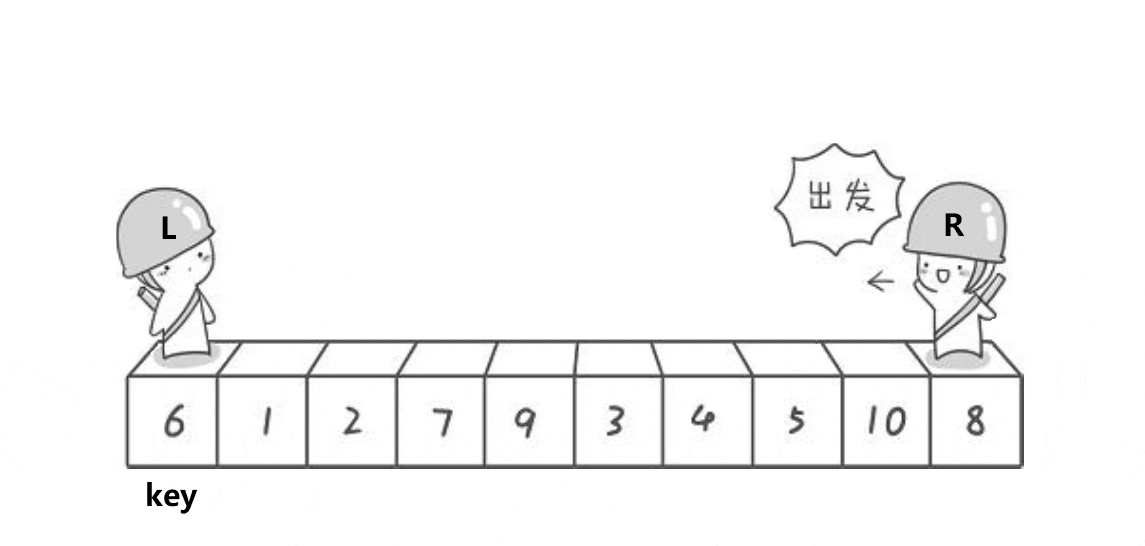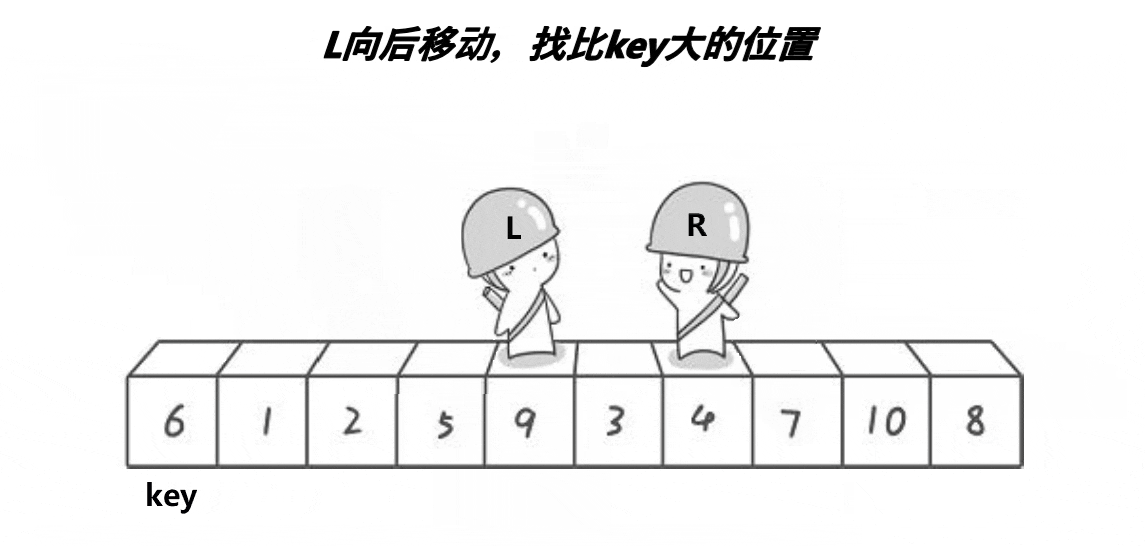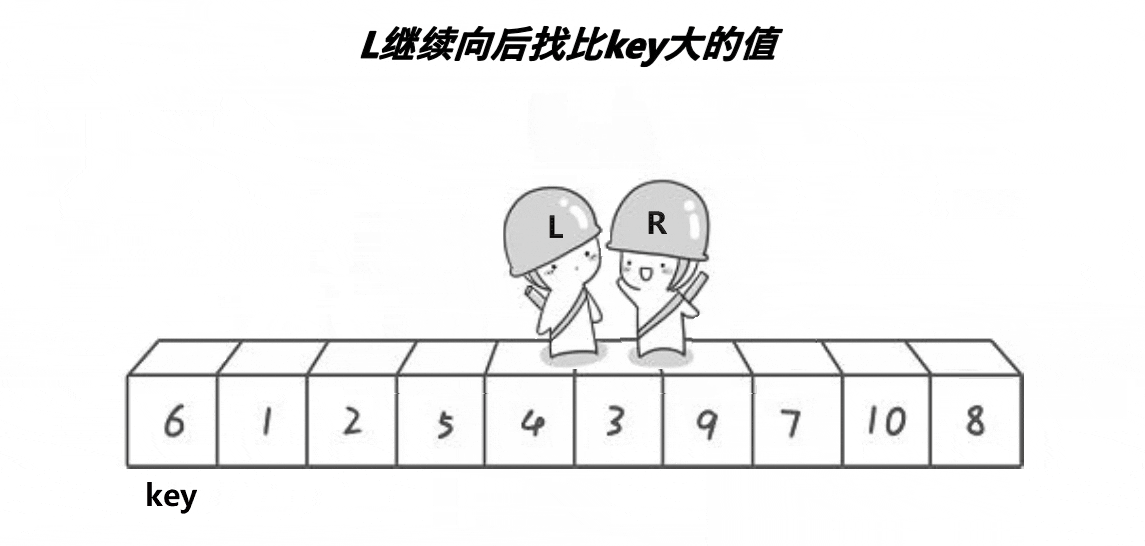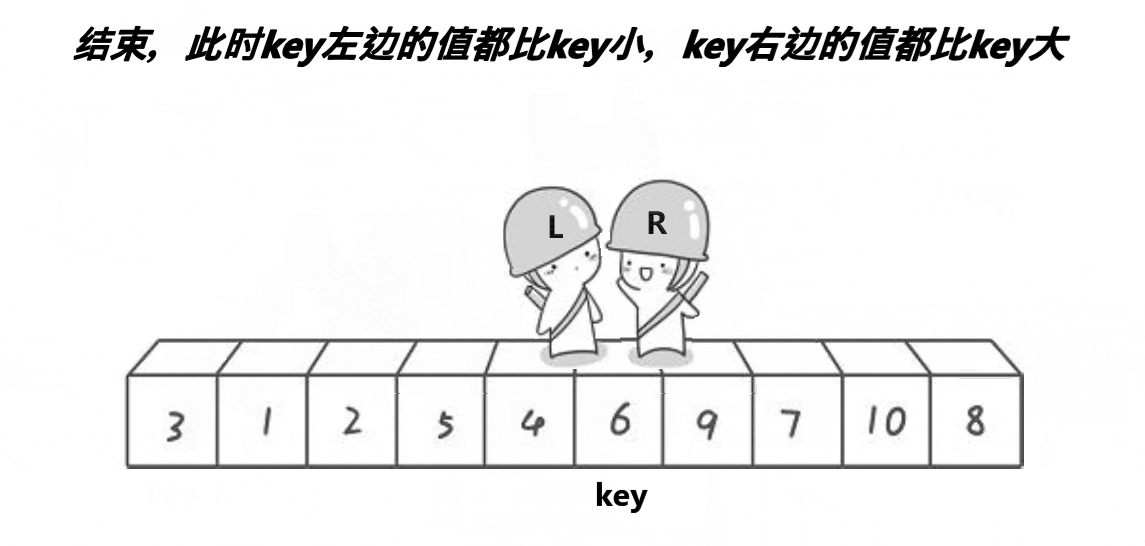
快排的思想是选出一个基准值key,然后把这个值放入正确的位置(最终排好序要去的位置)
例如
6,2,9,1,5,7,4这组数据我们选出6为
key值,然后将比6小的放左边,比6大的放右边这一趟下来,6就在正确的位置上了
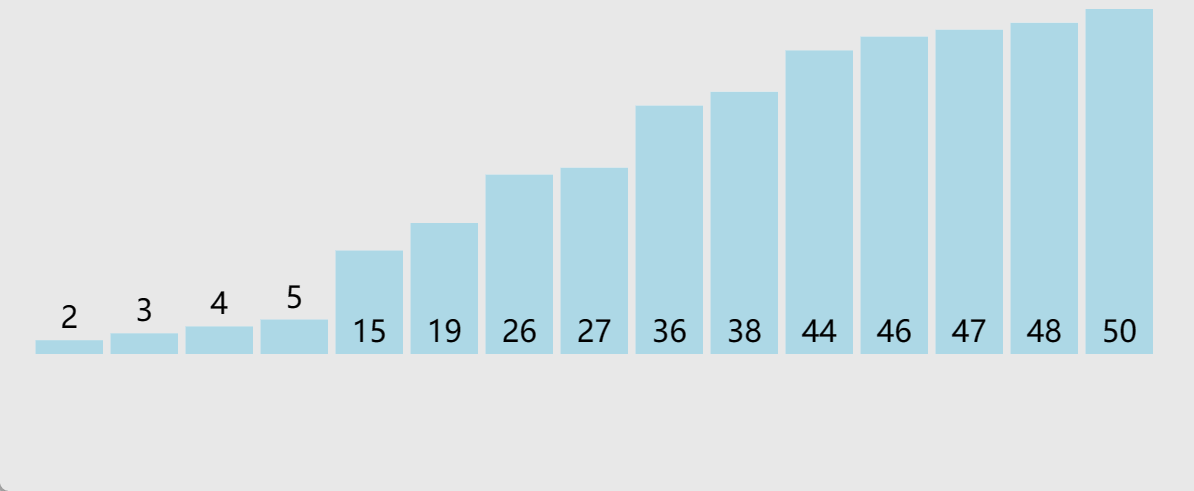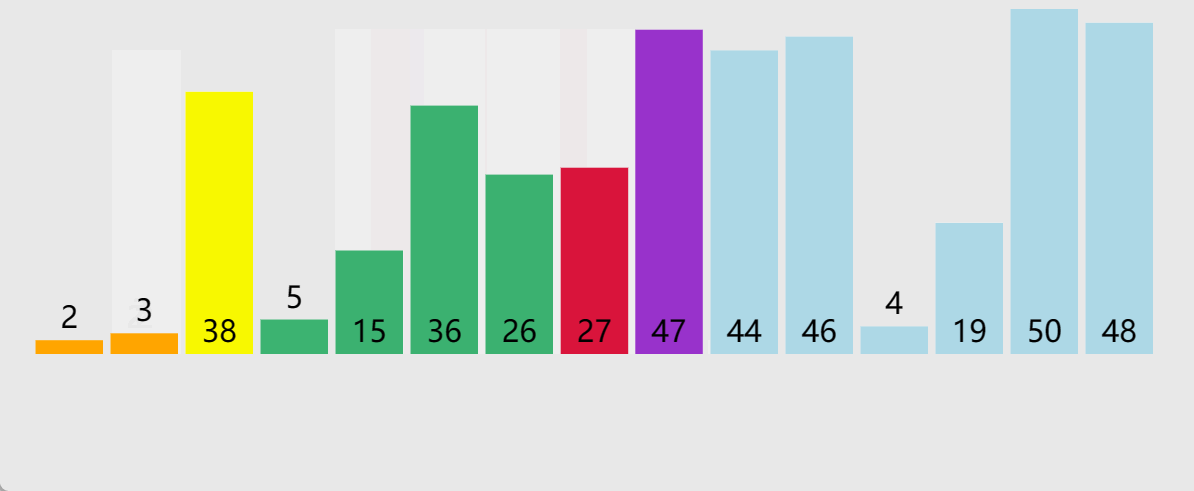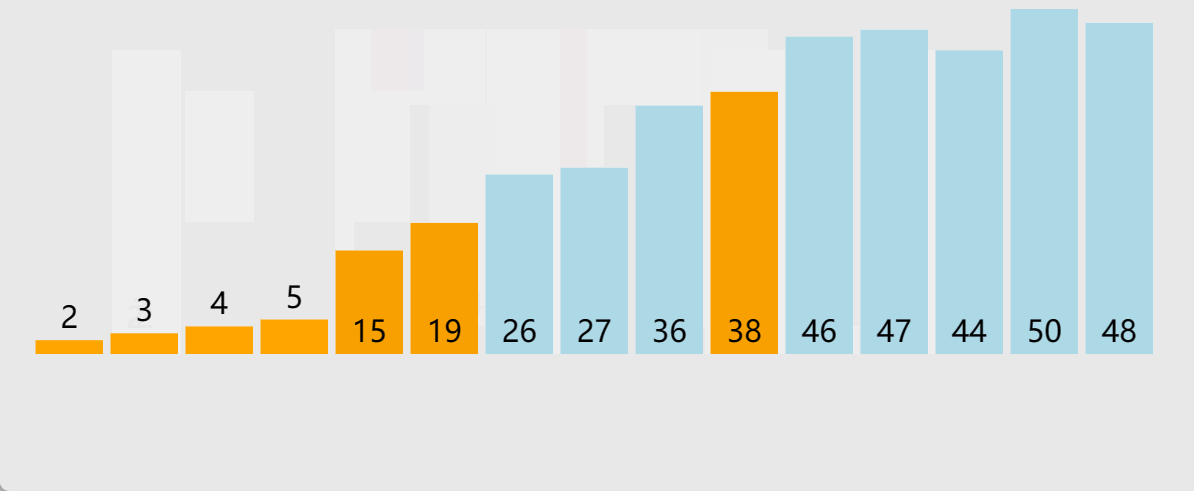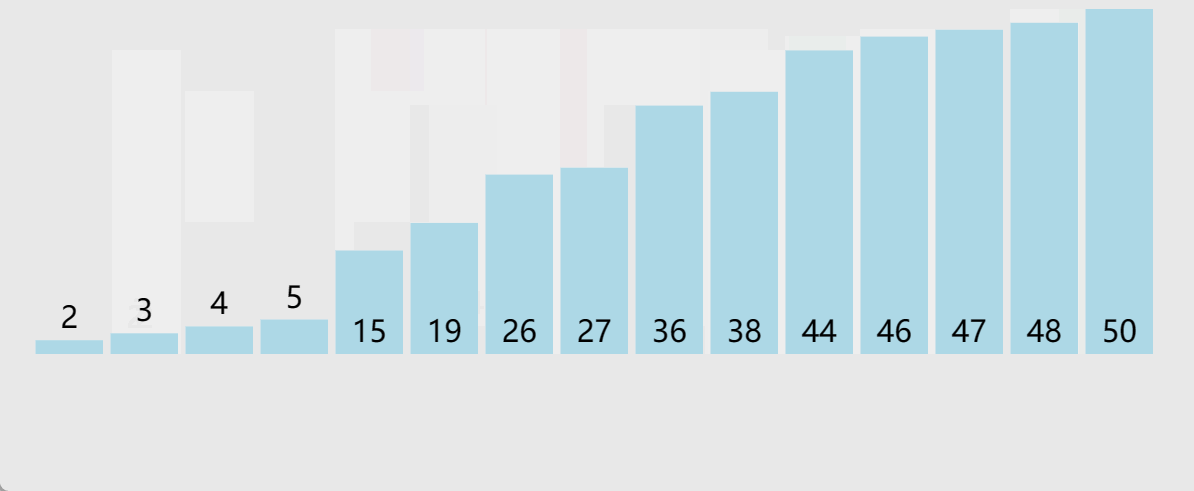
🎑hoare版本
//快速排序
void QuickSort(int* a, int left,int right)
{
if (left >= right)
return;
//记录起始
int begin = left;
int end = right;
//选取最左边为key值
int keyi = left;
while (left < right)
{
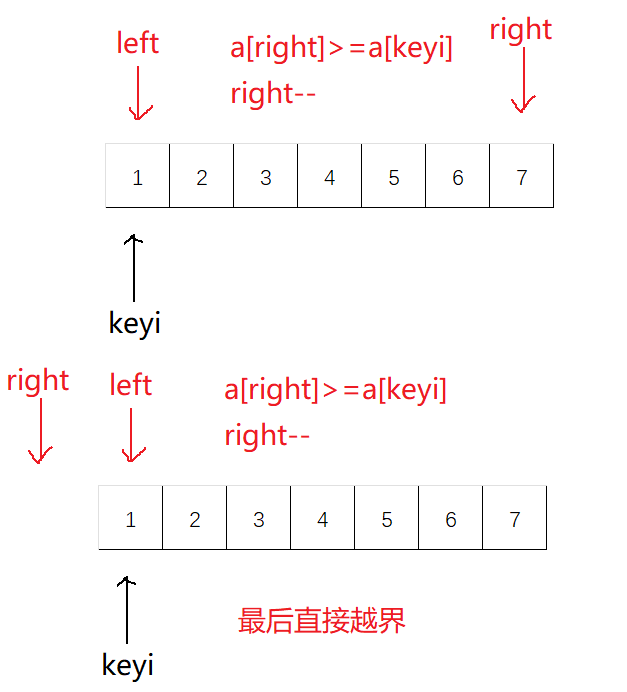
//选左 右先走 找小值
while (left<right && a[right] >= a[keyi])
{
right--;
}
while (left < right && a[left] <= a[keyi])
{
left++;
}
//交换两边的值
Swap(&a[left], &a[right]);
}
Swap(& a[keyi], & a[left]);
keyi = left;
//左右区间递归
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi+1, end);
}
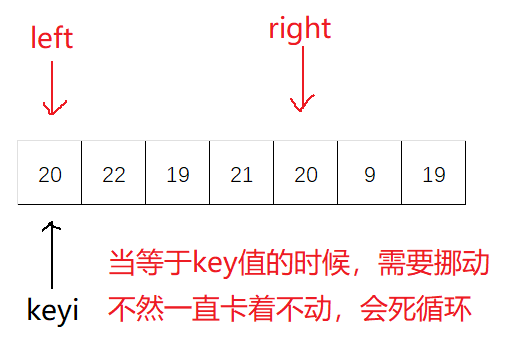
hoare版本为快排的最初始版本,这个版本不容易控制:
找大值/小值的时候,如果该值等于key值,也需要挪动,即
a[right] >= a[keyi]、a[left] <= a[keyi]
另外,判断条件还应加上
left<right,防止越界
左边作为
key,右边先走,这样就能保证相对位置比key要小或者就是key的位置右边作为
key,左边先走,相遇位置比key大或者就是key的位置已排序或者逆序的情况都是最糟糕的情况
有多少个数据,就有递归多少层栈帧,最终会导致栈溢出
-
随机选
key这个
keyi影响了快排的效率,只要keyi取的数,每次越接近于中间,那么每次就越接近于二分,所以我们可以考虑随机选key,这样就不必担心序列是否接近有序//快速排序 void QuickSort(int* a, int left,int right) { if (left >= right) return; //记录起始 int begin = left; int end = right; //left可能不是0,加上left int randi = left + (rand() % (right - left)); //还是选择左边为key,交换一下 Swap(&a[left], &a[randi]); //选取最左边为key值 int keyi = left; while (left < right) { //选左 右先走 找小值 while (left<right && a[right] >= a[keyi]) { right--; } //左边找大值 while (left < right && a[left] <= a[keyi]) { left++; } //交换两边的值 Swap(&a[left], &a[right]); } Swap(& a[keyi], & a[left]); keyi = left; //[begin,keyi-1] keyi [keyi+1,end] //左右区间递归 QuickSort(a, begin, keyi - 1); QuickSort(a, keyi+1, end); } -
三数取中
int GetMidNumi(int* a, int left, int right) { int mid = (left + right) / 2; if (a[left] < a[mid]) { if (a[mid] < a[right]) return mid; else if (a[left] > a[right]) return left; else return right; } else //a[left] >a[mid] { if (a[mid] > a[right]) return mid; else if (a[left] < a[right]) return left; else return right; } } int Partition1(int* a, int left, int right) { //三数取中 开始 中间 末尾 选中间值 int midi = GetMidNumi(a, left, right); if (midi != left) Swap(&a[left], &a[midi]); //选取最左边为key值 int keyi = left; while (left < right) { //选左 右先走 找小值 while (left < right && a[right] >= a[keyi]) { right--; } //左边找大值 while (left < right && a[left] <= a[keyi]) { left++; } Swap(&a[left], &a[right]); } Swap(&a[keyi], &a[left]); keyi = left; return keyi; } void QuickSort(int* a, int left, int right) { if (left > right) return; int keyi = Partition1(a, left, right); QuickSort(a, left, keyi - 1); QuickSort(a, keyi + 1, right); }
🎑挖坑法
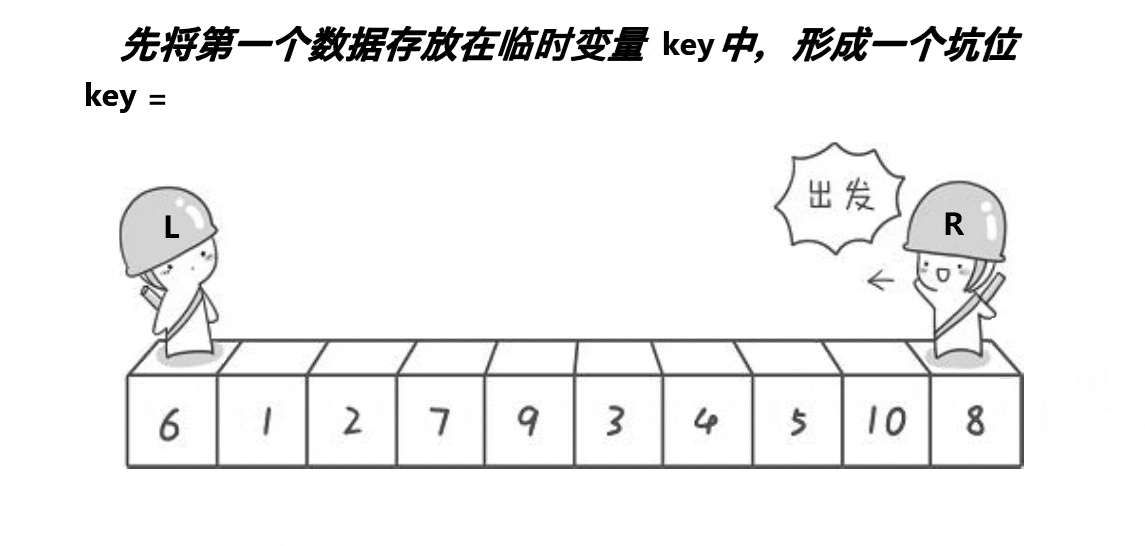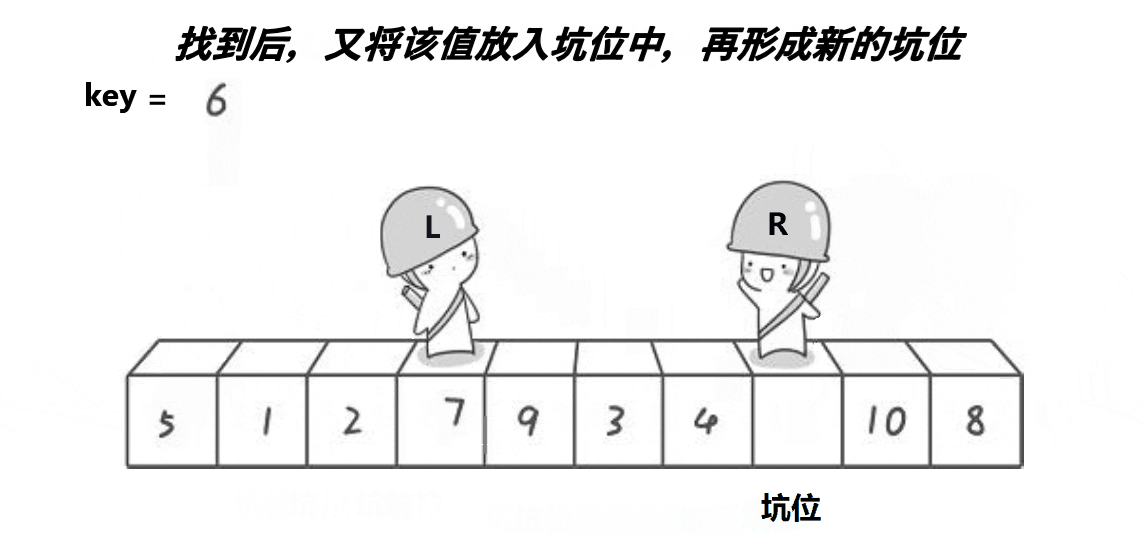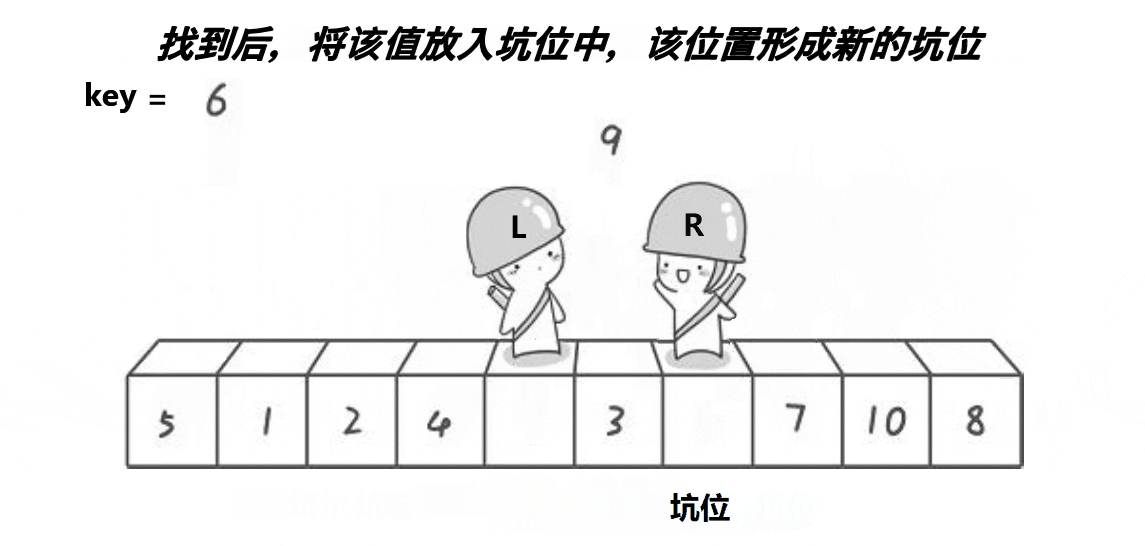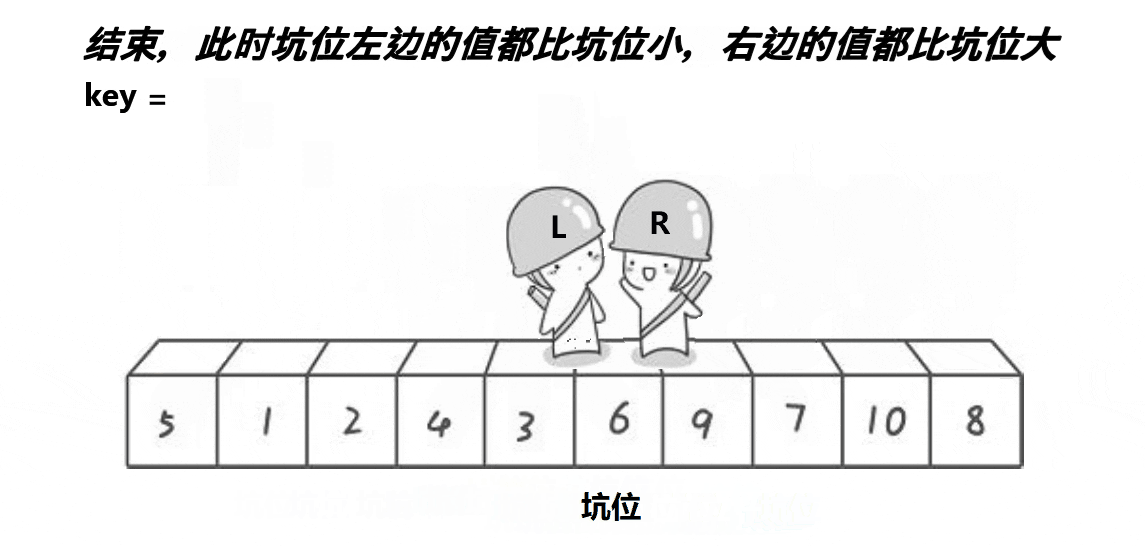
基本思路不边,只是这个更好理解,挖坑填坑、挖坑填坑,最后相遇位置一定是坑位
//挖坑
int Partition2(int* a, int left, int right)
{
//三数取中 开始 中间 末尾 选中间值
int midi = GetMidNumi(a, left, right);
if (midi != left)
Swap(&a[left], &a[midi]);
//选取最左边为key值
int key = a[left];
int hole = left;
while (left < right)
{
//选左 右先走 找小值
while (left < right && a[right] >= key)
{
right--;
}
//填坑
a[hole] = a[right];
//挖坑
hole = right;
//左边找大值
while (left < right && a[left] <= key)
{
left++;
}
a[hole] = a[left];
hole = left;
}
a[hole] = key;
return hole;
}
void QuickSort(int* a, int left, int right)
{
if (left > right)
return;
int keyi = Partition2(a, left, right);
QuickSort(a, left, keyi - 1);
QuickSort(a, keyi + 1, right);
}
🎑前后指针
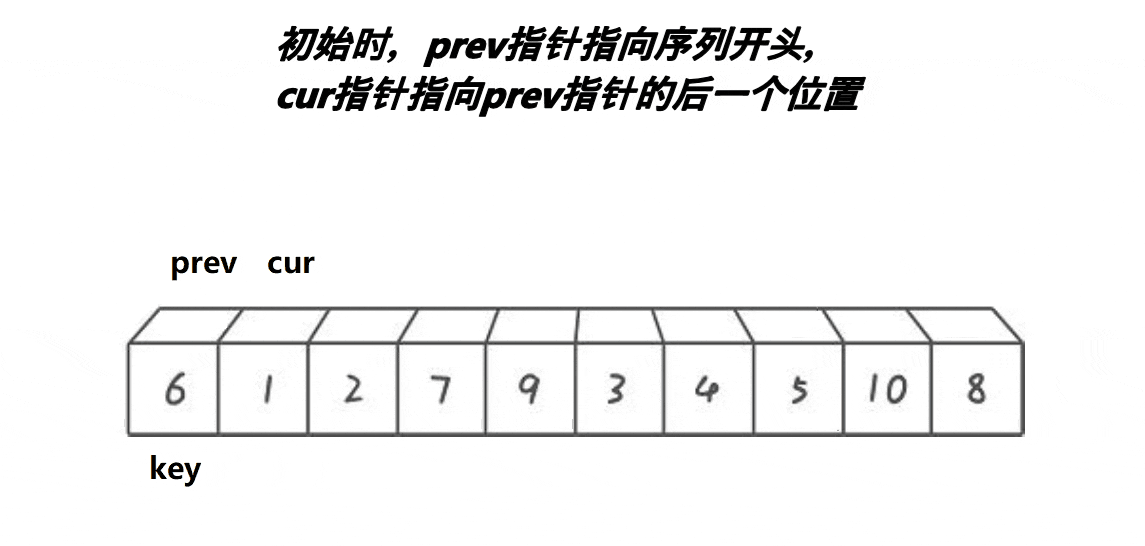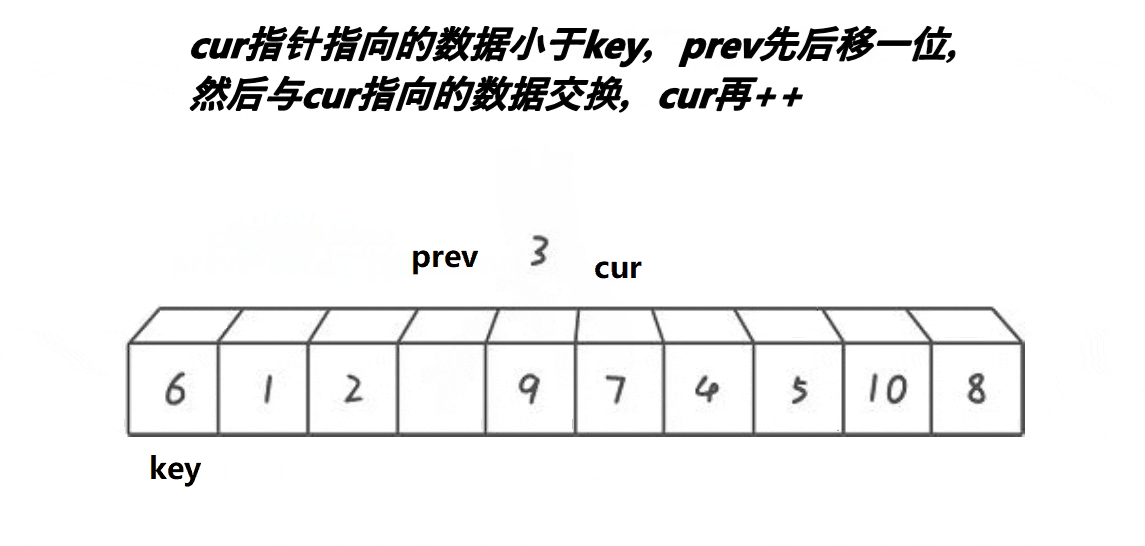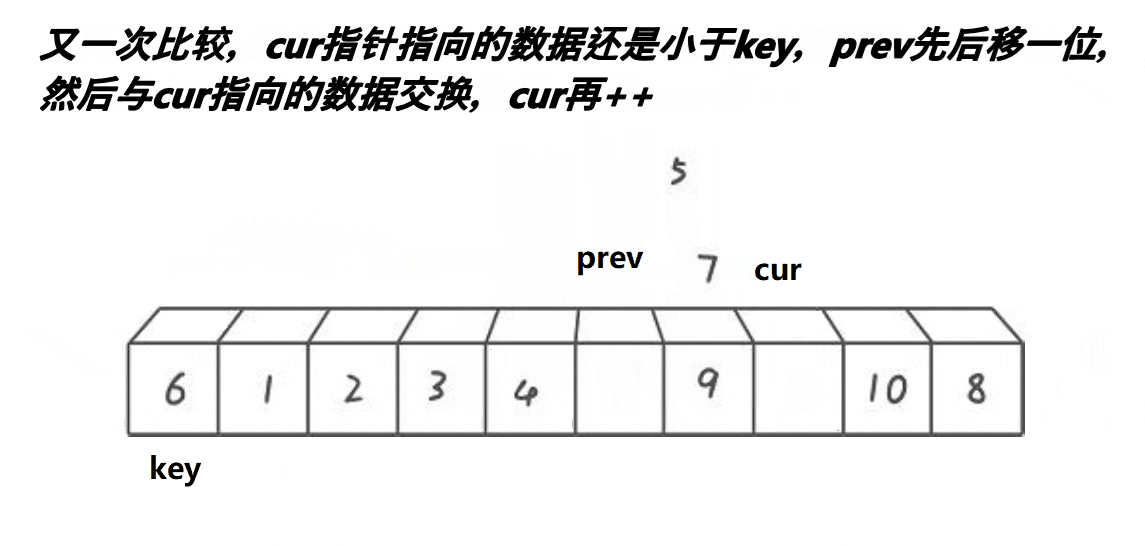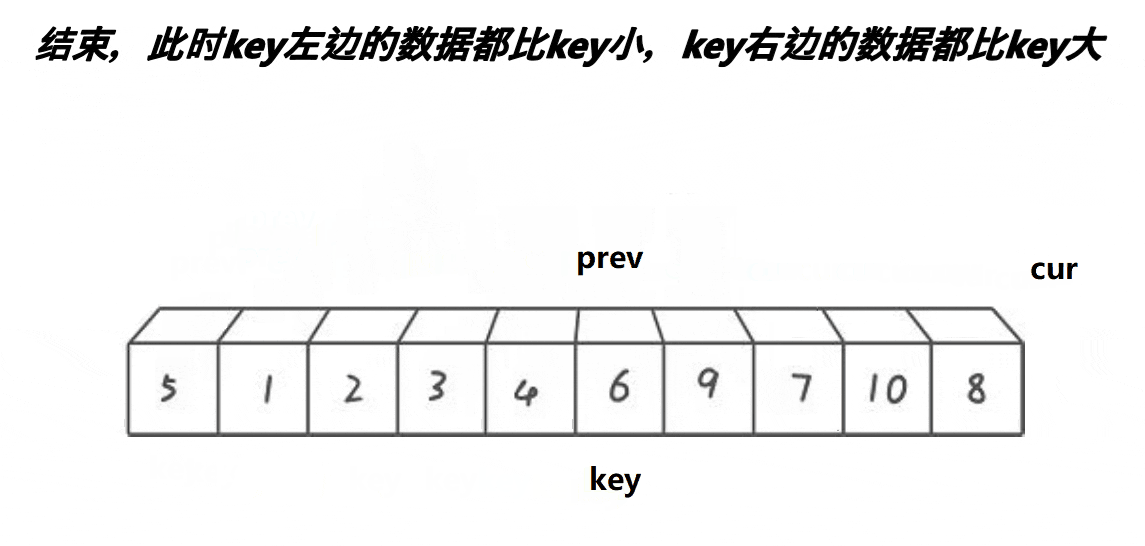
- cur找的值比
key小,++prev,cur与prev位置的值交换,++cur - cur找的值比
key大,++cur
//前后指针
int Partition3(int* a, int left, int right)
{
//三数取中 开始 中间 末尾 选中间值
int midi = GetMidNumi(a, left, right);
if (midi != left)
Swap(&a[left], &a[midi]);
int keyi = left;
int prev = left;
int cur = left + 1;
while (cur <= right)
{
if (a[cur] < a[keyi] && ++prev != cur)
{
Swap(&a[prev], &a[cur]);
}
++cur;
}
Swap(&a[keyi], &a[prev]);
keyi = prev;
return keyi;
}
void QuickSort(int* a, int left, int right)
{
if (left > right)
return;
int keyi = Partition3(a, left, right);
QuickSort(a, left, keyi - 1);
QuickSort(a, keyi + 1, right);
}
🎑小区间优化
当大量的数据递归到小量数据的时候,递归就会很麻烦,所以当数据量较小的时候,我们可以采用插入排序进行辅助,直接将这一小段数据排成有序
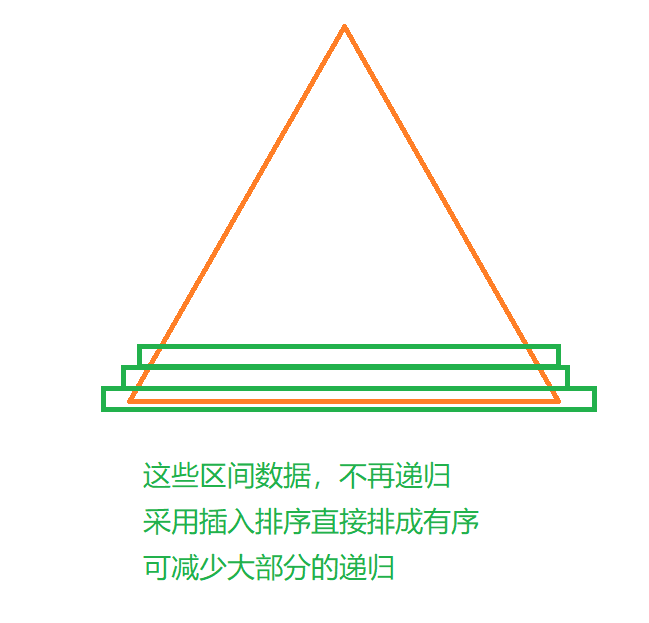
#define INSERTION_SORT_THRESHOLD 10
void QuickSort(int* a, int left, int right)
{
if (left > right)
return;
//区间自己决定 一般采用10左右
if ((right - left + 1) > INSERTION_SORT_THRESHOLD)
{
int keyi = Partition2(a, left, right);
QuickSort(a, left, keyi - 1);
QuickSort(a, keyi + 1, right);
}
else
InsertSort(a + left, right - left + 1);
}
🎑非递归
模拟递归,将区间放入栈
void QuickSortNonR(int* a, int left, int right)
{
//用C++的stl库
stack<int> st;
st.push(right);
st.push(left);
while (!st.empty())
{
int begin = st.top();
st.pop();
int end = st.top();
st.pop();
int keyi = Partition2(a, begin, end);
//[begin,keyi-1] keyi [keyi+1,end]
if (keyi + 1 < end)
{
st.push(end);
st.push(keyi + 1);
}
if (begin < keyi - 1)
{
st.push(keyi - 1);
st.push(begin);
}
}
}
快排特性:
时间复杂度:O(N*logN)
快排比较像二叉树
单趟排序的时间复杂度为O(N),而递归的深度是O(logN),合计起来就是O(N*logN)这个量级
空间复杂度:O(logN)
稳定性:不稳定
🎀4. 归并排序
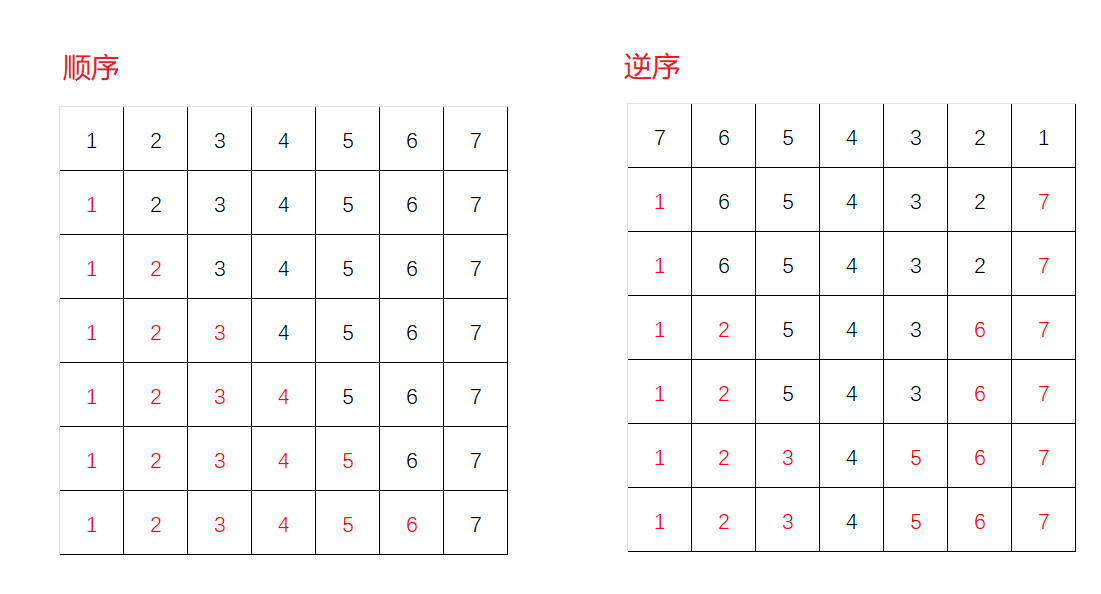
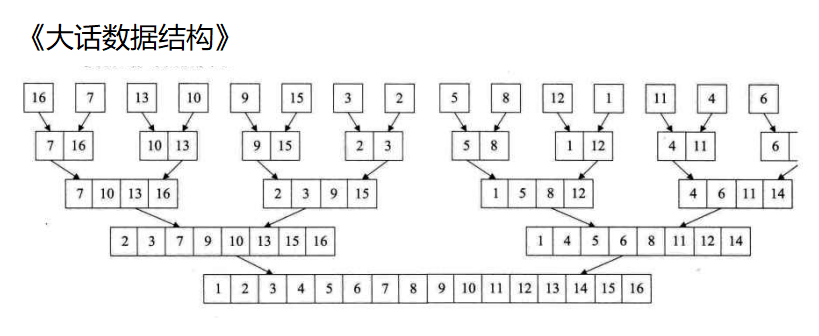
归并排序的思想就是分治,将一个序列看作n个子序列,然后将子序列排好序之后两两归并,这个方法也成为二路归并
🎁4.1 递归
//归并排序
void _MergeSort(int* a, int begin, int end, int* tmp)
{
if (begin >= end)
return;
//分割区间
int mid = (begin + end) / 2;
//子区间递归排序
//[begin,mid] [mid+1,end]
_MergeSort(a, begin, mid, tmp);
_MergeSort(a, mid+1, end, tmp);
//归并
int begin1 = begin;
int begin2 = mid+1;
int end1 = mid;
int end2 = end;
int index = begin;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
tmp[index++] = a[begin1++];
else
tmp[index++] = a[begin2++];
}
//防止未结束的区间
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
//拷贝回原序列
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + (int)1));
}
void MergeSort(int* a, int n)
{
//开辟临时空间
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail\n");
exit(-1);
}
_MergeSort(a, 0, n - 1, tmp);
free(tmp);
}
🎁4.2 非递归

归并排序的非递归需要注意的就是边界问题,我们每次都是分为2组归并,如果是单数的话,会发生越界行为,所以要查看这两组的区间:
-
begin1,取值为i,所以肯定不会越界 -
end1如果越界,后面的肯定越界,无需进行归并 -
end1没有越界,begin2如果越界,无需进行归并 -
begin2没有越界,end2越界,需要归并,修正end2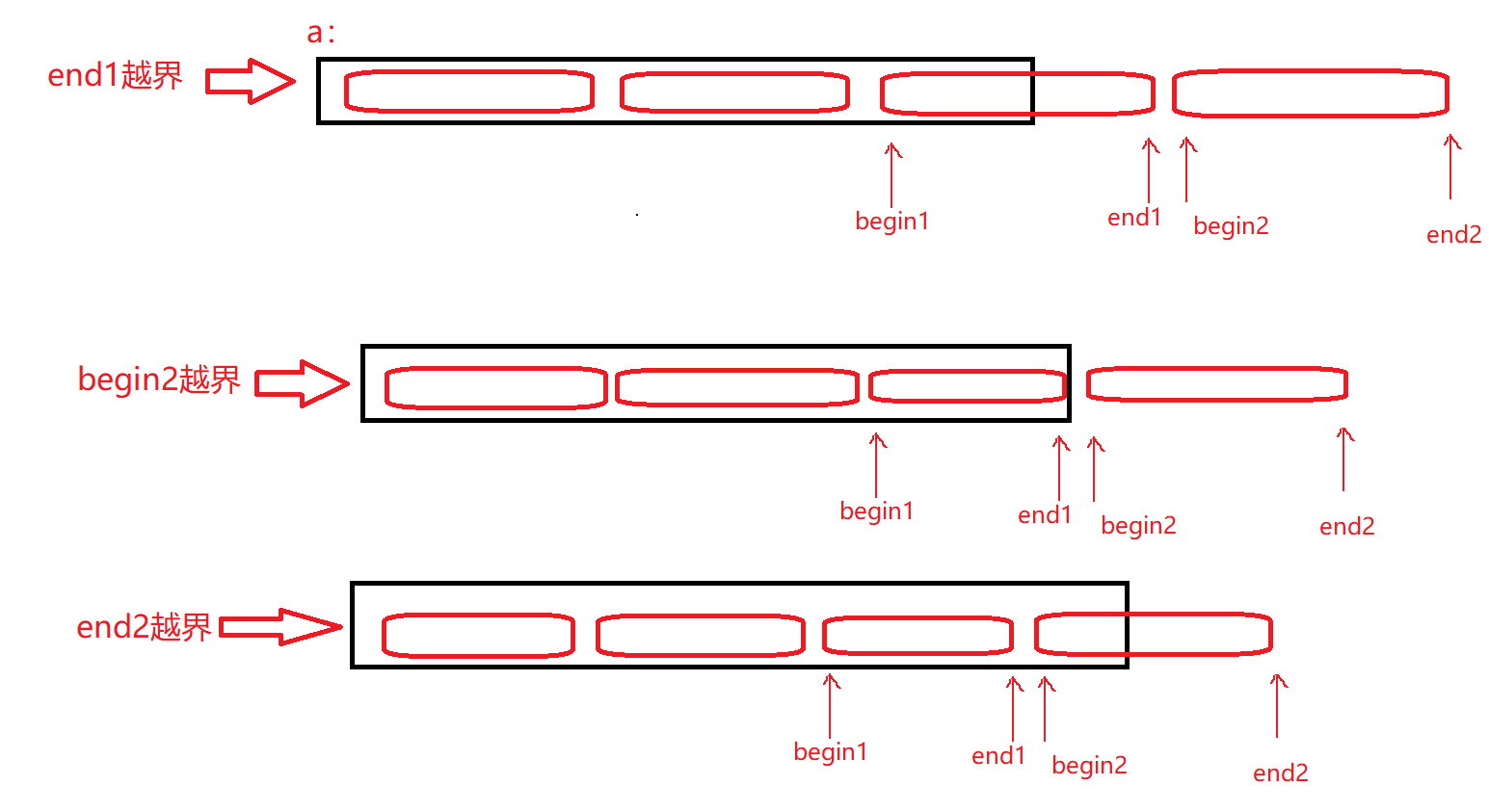
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail\n");
exit(-1);
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
//归并
int begin1 = i;
int end1 = i + gap - 1;
int begin2 = i + gap;
int end2 = i + 2 * gap - 1;
//修正 外面一次性拷贝
//if (end1 >= n)
//{
// //不归并
// end1 = n - 1;
// //给一个不存在区间
// begin2 = n;
// end2 = n - 1;
//}
//else if (begin2 >= n)
//{
// //不归并 修正成不存在的区间
// begin2 = n;
// end2 = n - 1;
//}
//else if (end2 >= n)
//{
// //修正
// end2 = n - 1;
//}
if (end1 >= n || begin2 >= n)
{
break;
}
if (end2 >= n)
{
end2 = n - 1;
}
int index = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
tmp[index++] = a[begin1++];
else
tmp[index++] = a[begin2++];
}
//防止未结束的区间
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
}
//外面拷贝,一把梭哈
//memcpy(a, tmp, sizeof(int) * n);
gap *= 2;
}
free(tmp);
}
归并排序特性:
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
- 归并排序更多解决的是磁盘中的外排序问题
🎫5. 性能测试
测试性能我们开
release版本,火力全开;测试环境为Linux的g++
本次只是简单的进行测试,可能会有偶然性
void TestOP()
{
srand(time(0));
const int N = 10000; //1w
//const int N = 100000; //10w
//const int N = 5000000; //100w
//const int N = 10000000; //1000w
//const int N = 100000000; //1亿
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2 = (int*)malloc(sizeof(int) * N);
int* a3 = (int*)malloc(sizeof(int) * N);
int* a4 = (int*)malloc(sizeof(int) * N);
int* a5 = (int*)malloc(sizeof(int) * N);
int* a6 = (int*)malloc(sizeof(int) * N);
int* a7 = (int*)malloc(sizeof(int) * N);
int* a8 = (int*)malloc(sizeof(int) * N);
for (int i = 0; i < N; i++)
{
a1[i] = rand();
a2[i] = a1[i];
a3[i] = a1[i];
a4[i] = a1[i];
//a4[i] = 2;
a5[i] = a1[i];
a6[i] = a1[i];
a7[i] = a1[i];
a8[i] = a1[i];
}
int begin1 = clock();
InsertSort(a1, N);
int end1 = clock();
int begin2 = clock();
ShellSort(a2, N);
int end2 = clock();
int begin3 = clock();
SelectSort(a3, N);
int end3 = clock();
int begin4 = clock();
HeapSort(a3, N);
int end4 = clock();
int begin5 = clock();
BubbleSort(a5, N);
int end5 = clock();
int begin6 = clock();
QuickSort(a4, 0, N - 1);
int end6 = clock();
int begin7 = clock();
MergeSort(a6, N);
int end7 = clock();
std::vector<int> v(a8, a8 + N);
int begin8 = clock();
std::sort(v.begin(),v.end());
int end8 = clock();
printf("InsertSort:%d\n", end1 - begin1);
printf("ShellSort:%d\n", end2 - begin2);
printf("SeletSort:%d\n", end3 - begin3);
printf("HeapSort:%d\n", end4 - begin4);
printf("BubbleSort:%d\n", end5 - begin5);
printf("QuickSort:%d\n", end6 - begin6);
printf("MergeSort:%d\n", end7 - begin7);
printf("STLSort:%d\n", end8 - begin8);
free(a1);
free(a2);
free(a3);
free(a4);
free(a5);
free(a6);
free(a7);
free(a8);
}
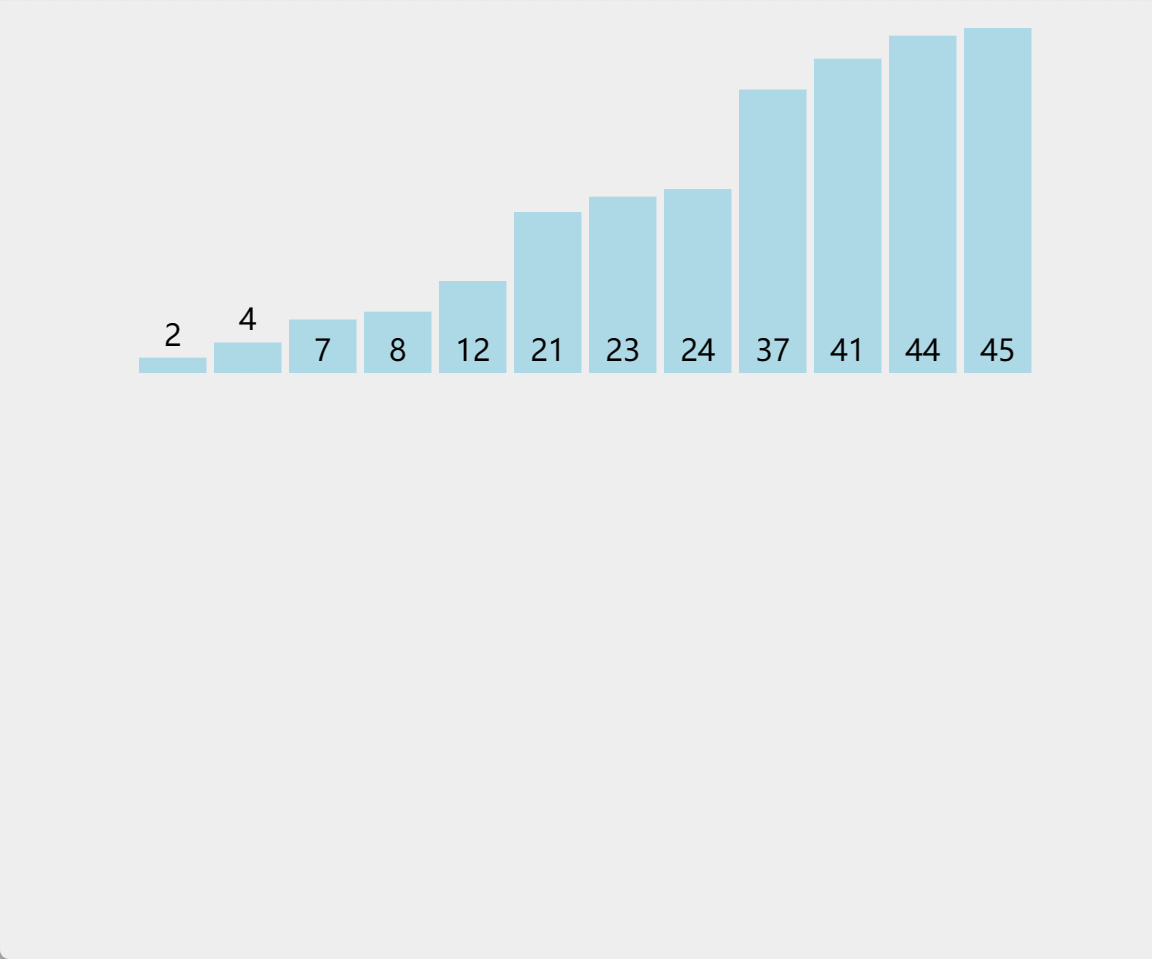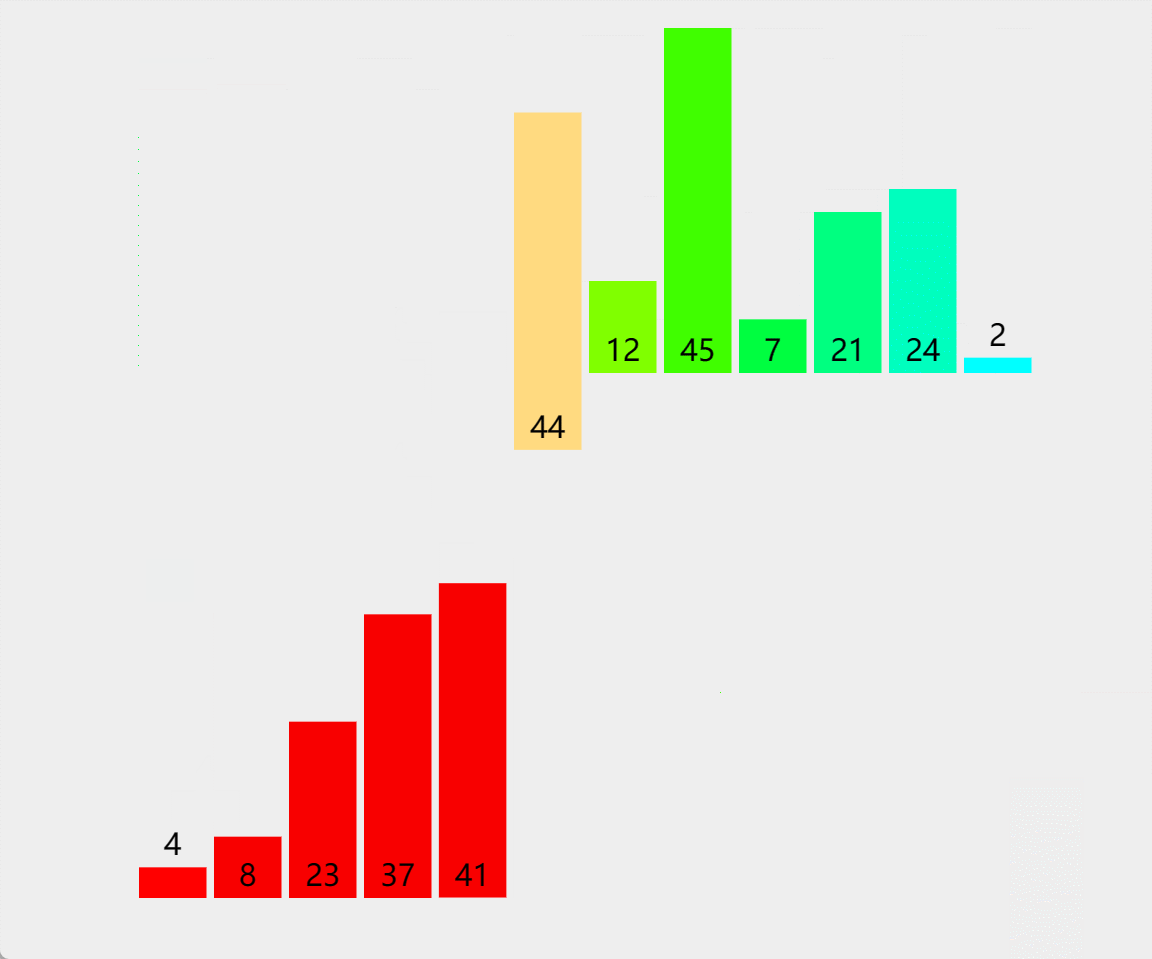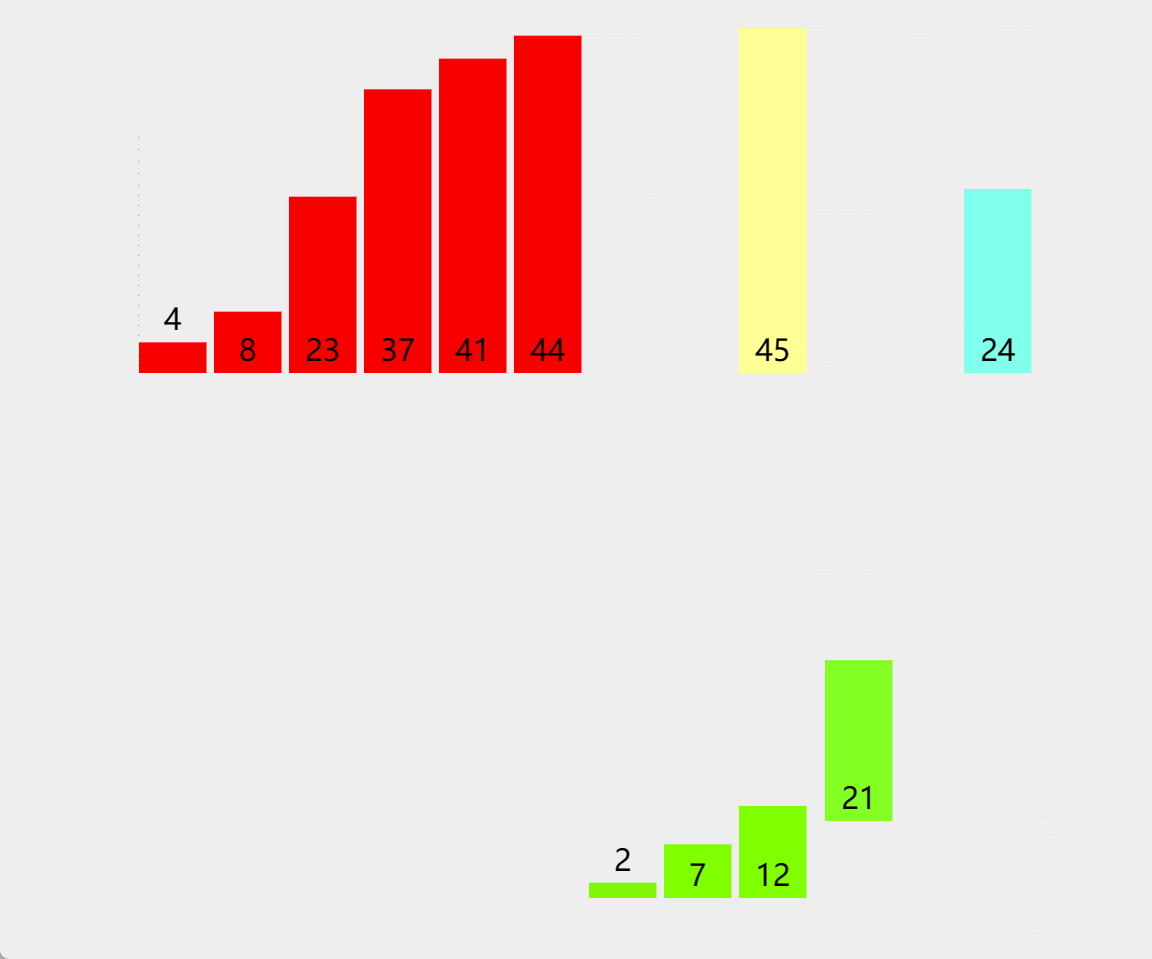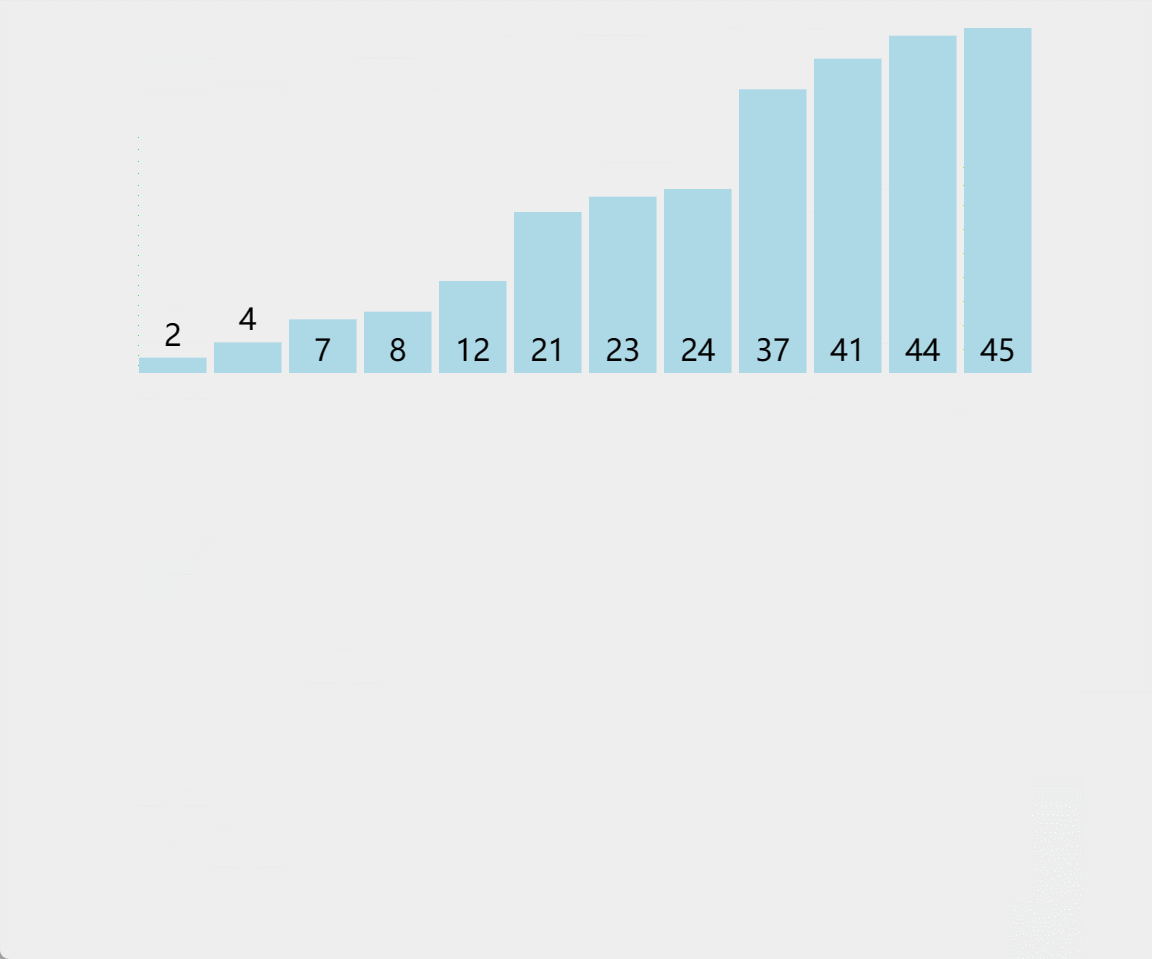
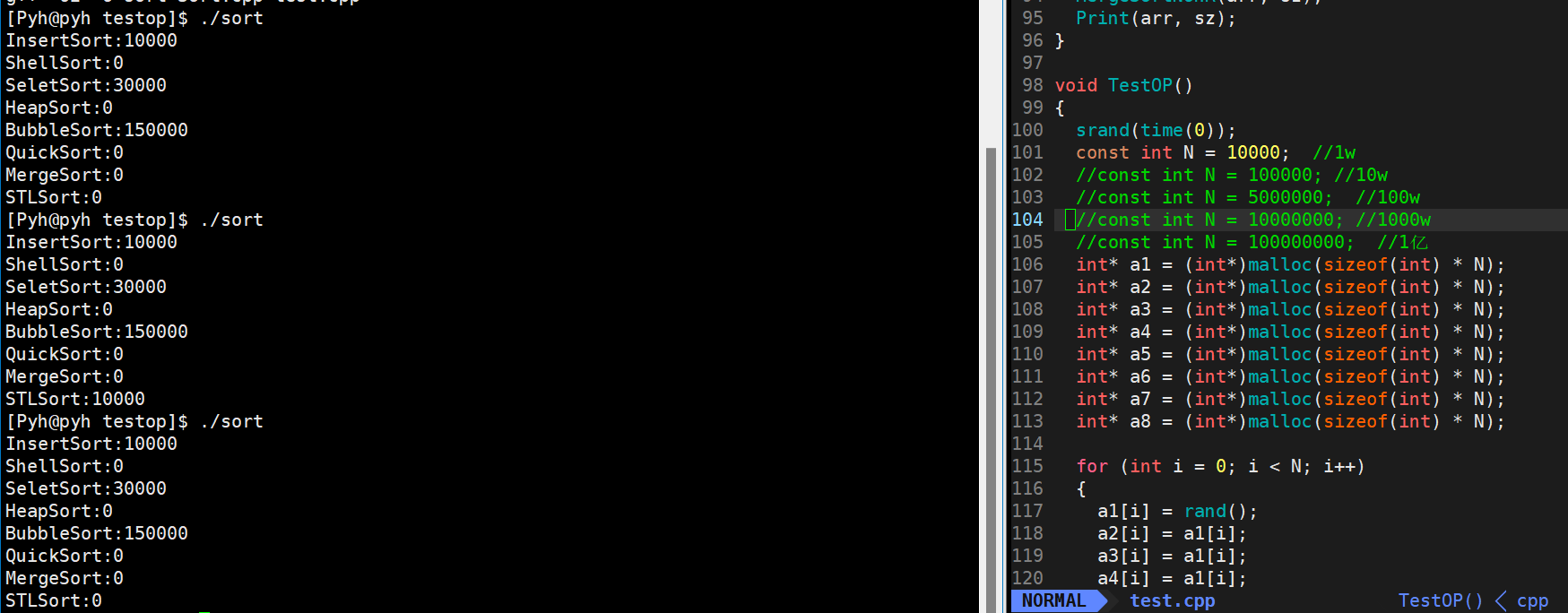
🎖5.1 1w数据
在1w数据这个量级,对于希尔排序、堆排序、快排、归并排序,都是挠痒痒,忽略不计
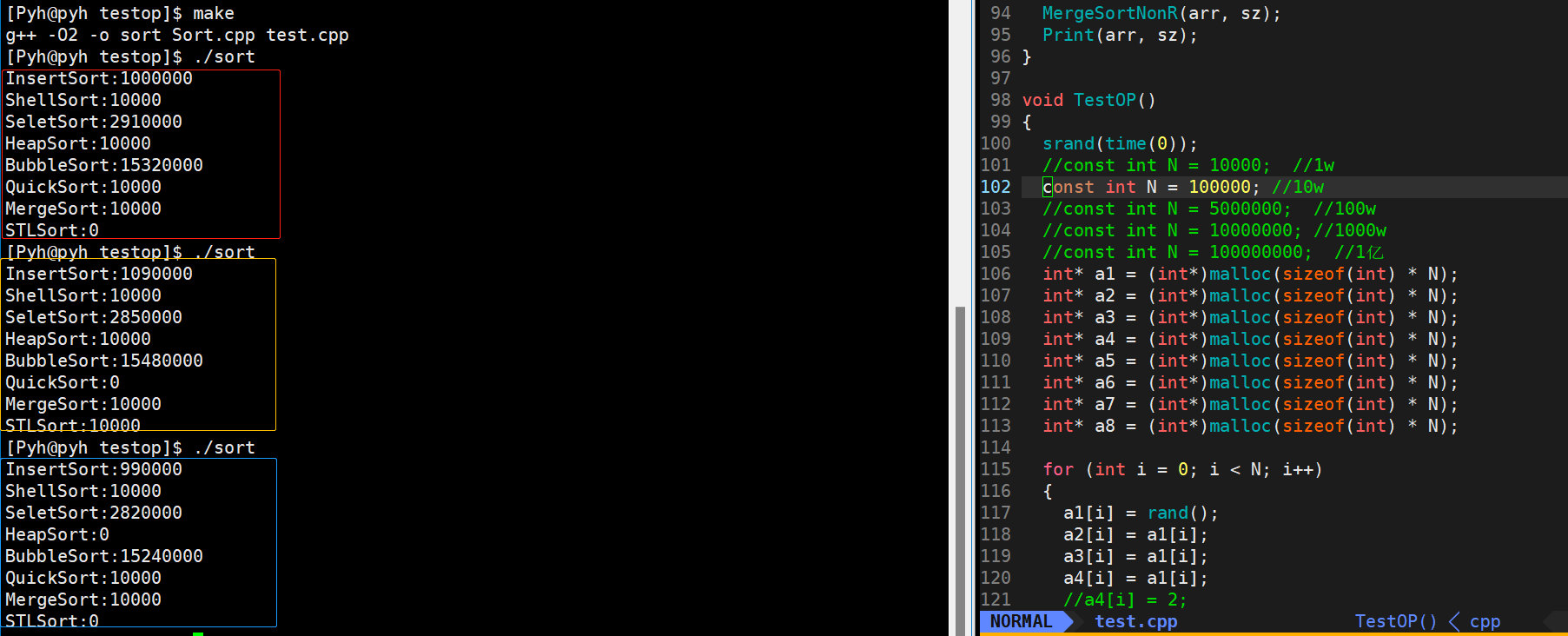
🎖5.2 10w数据
在10w这个量级,显然直接插入排序、直接选择排序、冒泡排序都以不堪重负,而对于这些时间复杂度度在O(N*logN)量级的排序,才刚刚开始
🎖5.3 100w数据
到了100w这个量级,就不再对量级为O(N2)进行测试了,他们坐小孩儿那桌
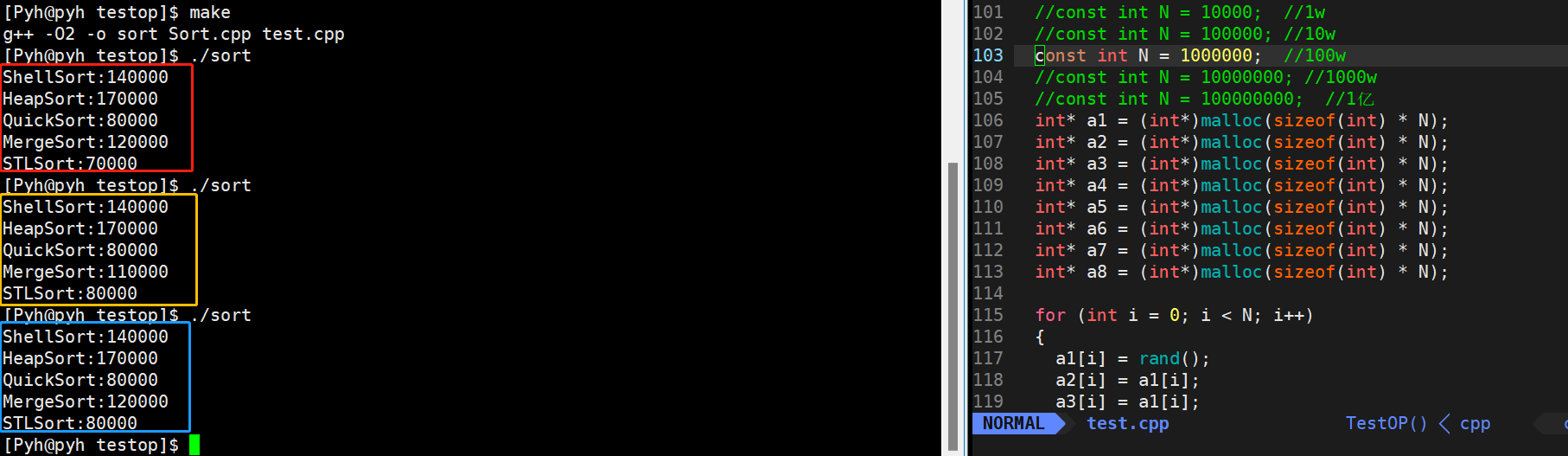
这里可以看出,快排还得是快排
🎖5.4 1000w数据
到1000w这个量级,堆排序就有点扛不住了
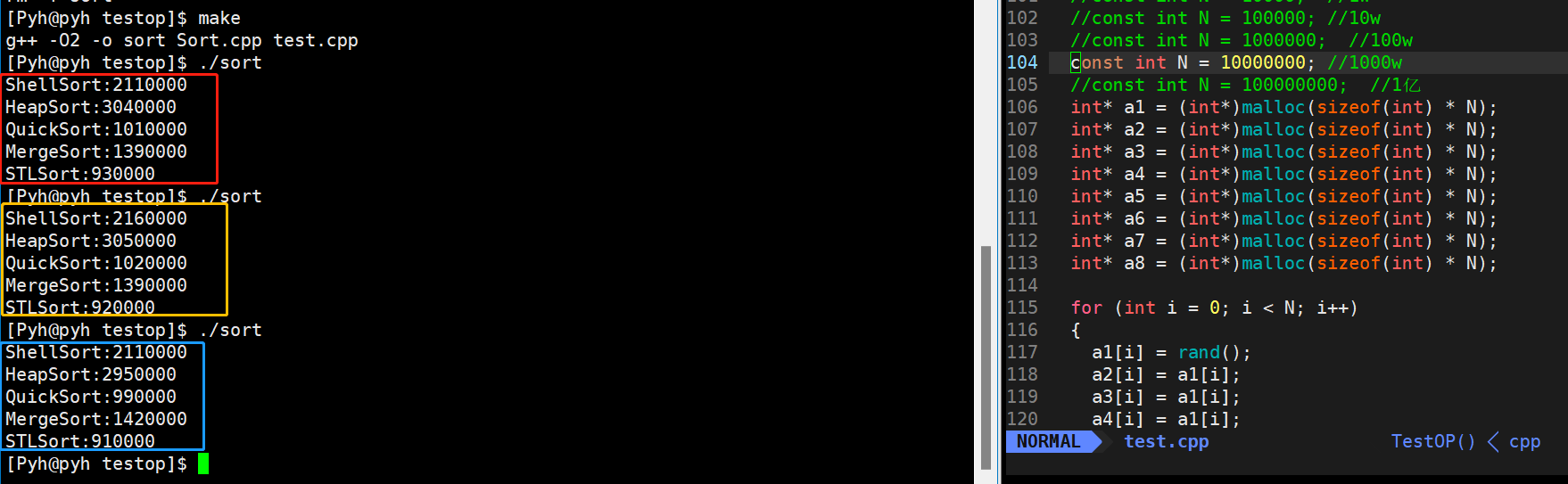
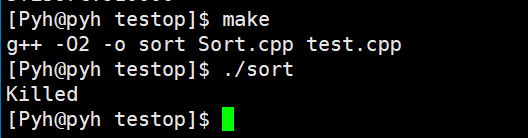
🎖5.5 1亿数据
在一亿这个量级,服务器有点跑不动了
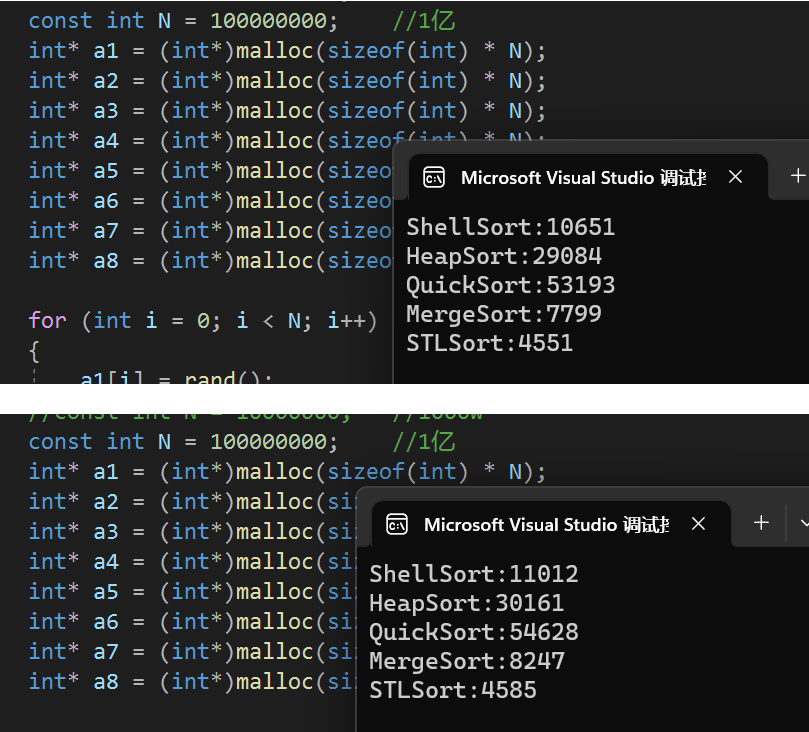
换到Windows环境参考,这个具体还得看机器和优化,不是特别具有参考意义,但可以看一下C++库里面的快排实现
那本期的分享就到这里,我们下期再见,如果还有下期的话。