给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。

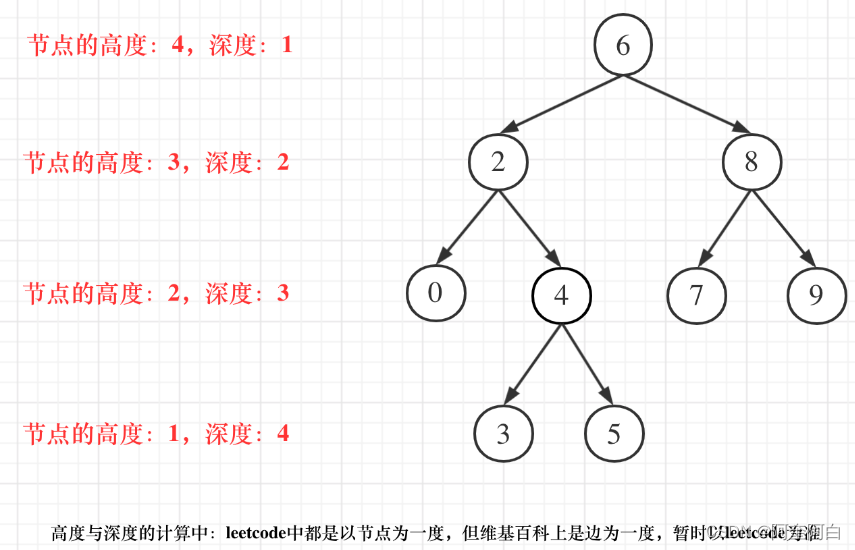
思路

求深度可以从上到下去查 所以需要前序遍历（中左右）

而高度只能从下到上去查，所以只能后序遍历（左右中）

递归法

1. 递归参数和返回值

参数：当前传入节点，返回值：以当前传入节点为根节点的树的高度

如何标记左右子树差值是否大于1？

若当前传入节点为根节点的二叉树不是平衡二叉树，返回高度没有意义。

定义返回-1表明已经不是平衡二叉树。

int getHeight(TreeNode* node)

2. 终止条件

递归的过程中依然是遇到空节点了为终止，返回0，表示当前节点为根节点的树高度为0

if(node == nullptr) return 0;

3. 单层递归逻辑

分别求出其左右子树的高度，然后如果差值小于等于1，则返回当前二叉树的高度，否则返回-1，表示已经不是二叉平衡树了。

int leftHeight = getHeight(node->left);
int rightHeight = getHeight(node->right);
if(leftHeight == -1) return -1;
if(rightHeight == -1) return -1;

return abs(leftHeight-rightHeight)>1?-1:1+max(leftHeight, rightHeight);

整体代码：

class Solution {
public:
    int getHeight(TreeNode* node){
        if(node == nullptr) return 0;
        int leftHeight = getHeight(node->left);
        int rightHeight = getHeight(node->right);
        if(leftHeight == -1) return -1;
        if(rightHeight == -1) return -1;

        return abs(leftHeight-rightHeight)>1?-1:1+max(leftHeight, rightHeight);
    }
    bool isBalanced(TreeNode* root) {
        return getHeight(root) == -1 ? false : true;
    }
};

迭代法

在求二叉树的最大深度中我们可以使用层序遍历来求深度，但是就不能直接用层序遍历来求高度了，这就体现出求高度和求深度的不同。